-
Notifications
You must be signed in to change notification settings - Fork 89
Added tasks 2144, 2145, 2146, 2147, 2148 #1073
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Merged
javadev
merged 2 commits into
javadev:main
from
ThanhNIT:tasks-2144-2145-21466-2147-2148
Jun 7, 2022
Merged
Changes from all commits
Commits
Show all changes
2 commits
Select commit
Hold shift + click to select a range
File filter
Filter by extension
Conversations
Failed to load comments.
Loading
Jump to
Jump to file
Failed to load files.
Loading
Diff view
Diff view
There are no files selected for viewing
21 changes: 21 additions & 0 deletions
21
src/main/java/g2101_2200/s2144_minimum_cost_of_buying_candies_with_discount/Solution.java
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,21 @@ | ||
| package g2101_2200.s2144_minimum_cost_of_buying_candies_with_discount; | ||
|
|
||
| // #Easy #Array #Sorting #Greedy #2022_06_07_Time_2_ms_(97.50%)_Space_41.4_MB_(99.04%) | ||
|
|
||
| import java.util.Arrays; | ||
|
|
||
| public class Solution { | ||
| public int minimumCost(int[] cost) { | ||
| Arrays.sort(cost); | ||
| int size = 0; | ||
| int sum = 0; | ||
| for (int i = cost.length - 1; i >= 0; i--) { | ||
| size++; | ||
| if (size % 3 != 0) { | ||
| sum += cost[i]; | ||
| } | ||
| } | ||
|
|
||
| return sum; | ||
| } | ||
| } |
58 changes: 58 additions & 0 deletions
58
...in/java/g2101_2200/s2144_minimum_cost_of_buying_candies_with_discount/readme.md
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,58 @@ | ||
| 2144\. Minimum Cost of Buying Candies With Discount | ||
|
|
||
| Easy | ||
|
|
||
| A shop is selling candies at a discount. For **every two** candies sold, the shop gives a **third** candy for **free**. | ||
|
|
||
| The customer can choose **any** candy to take away for free as long as the cost of the chosen candy is less than or equal to the **minimum** cost of the two candies bought. | ||
|
|
||
| * For example, if there are `4` candies with costs `1`, `2`, `3`, and `4`, and the customer buys candies with costs `2` and `3`, they can take the candy with cost `1` for free, but not the candy with cost `4`. | ||
|
|
||
| Given a **0-indexed** integer array `cost`, where `cost[i]` denotes the cost of the <code>i<sup>th</sup></code> candy, return _the **minimum cost** of buying **all** the candies_. | ||
|
|
||
| **Example 1:** | ||
|
|
||
| **Input:** cost = [1,2,3] | ||
|
|
||
| **Output:** 5 | ||
|
|
||
| **Explanation:** We buy the candies with costs 2 and 3, and take the candy with cost 1 for free. | ||
|
|
||
| The total cost of buying all candies is 2 + 3 = 5. This is the **only** way we can buy the candies. | ||
|
|
||
| Note that we cannot buy candies with costs 1 and 3, and then take the candy with cost 2 for free. | ||
|
|
||
| The cost of the free candy has to be less than or equal to the minimum cost of the purchased candies. | ||
|
|
||
| **Example 2:** | ||
|
|
||
| **Input:** cost = [6,5,7,9,2,2] | ||
|
|
||
| **Output:** 23 | ||
|
|
||
| **Explanation:** The way in which we can get the minimum cost is described below: | ||
|
|
||
| - Buy candies with costs 9 and 7 | ||
|
|
||
| - Take the candy with cost 6 for free | ||
|
|
||
| - We buy candies with costs 5 and 2 | ||
|
|
||
| - Take the last remaining candy with cost 2 for free | ||
|
|
||
| Hence, the minimum cost to buy all candies is 9 + 7 + 5 + 2 = 23. | ||
|
|
||
| **Example 3:** | ||
|
|
||
| **Input:** cost = [5,5] | ||
|
|
||
| **Output:** 10 | ||
|
|
||
| **Explanation:** Since there are only 2 candies, we buy both of them. There is not a third candy we can take for free. | ||
|
|
||
| Hence, the minimum cost to buy all candies is 5 + 5 = 10. | ||
|
|
||
| **Constraints:** | ||
|
|
||
| * `1 <= cost.length <= 100` | ||
| * `1 <= cost[i] <= 100` |
37 changes: 37 additions & 0 deletions
37
src/main/java/g2101_2200/s2145_count_the_hidden_sequences/Solution.java
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,37 @@ | ||
| package g2101_2200.s2145_count_the_hidden_sequences; | ||
|
|
||
| // #Medium #Array #Prefix_Sum #2022_06_07_Time_7_ms_(36.03%)_Space_111.3_MB_(13.23%) | ||
|
|
||
| public class Solution { | ||
| public int numberOfArrays(int[] diff, int lower, int upper) { | ||
| int n = diff.length; | ||
| if (lower == upper) { | ||
| for (int j : diff) { | ||
| if (j != 0) { | ||
| return 0; | ||
| } | ||
| } | ||
| } | ||
| int max = -(int) 1e9; | ||
| int min = (int) 1e9; | ||
| int[] hidden = new int[n + 1]; | ||
| hidden[0] = 0; | ||
| for (int i = 1; i <= n; i++) { | ||
| hidden[i] = hidden[i - 1] + diff[i - 1]; | ||
| } | ||
| for (int i = 0; i <= n; i++) { | ||
| if (hidden[i] > max) { | ||
| max = hidden[i]; | ||
| } | ||
| if (hidden[i] < min) { | ||
| min = hidden[i]; | ||
| } | ||
| } | ||
| int low = lower - min; | ||
| int high = upper - max; | ||
| if (low > high) { | ||
| return 0; | ||
| } | ||
| return (high - low) + 1; | ||
| } | ||
| } | ||
61 changes: 61 additions & 0 deletions
61
src/main/java/g2101_2200/s2145_count_the_hidden_sequences/readme.md
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,61 @@ | ||
| 2145\. Count the Hidden Sequences | ||
|
|
||
| Medium | ||
|
|
||
| You are given a **0-indexed** array of `n` integers `differences`, which describes the **differences** between each pair of **consecutive** integers of a **hidden** sequence of length `(n + 1)`. More formally, call the hidden sequence `hidden`, then we have that `differences[i] = hidden[i + 1] - hidden[i]`. | ||
|
|
||
| You are further given two integers `lower` and `upper` that describe the **inclusive** range of values `[lower, upper]` that the hidden sequence can contain. | ||
|
|
||
| * For example, given `differences = [1, -3, 4]`, `lower = 1`, `upper = 6`, the hidden sequence is a sequence of length `4` whose elements are in between `1` and `6` (**inclusive**). | ||
| * `[3, 4, 1, 5]` and `[4, 5, 2, 6]` are possible hidden sequences. | ||
| * `[5, 6, 3, 7]` is not possible since it contains an element greater than `6`. | ||
| * `[1, 2, 3, 4]` is not possible since the differences are not correct. | ||
|
|
||
| Return _the number of **possible** hidden sequences there are._ If there are no possible sequences, return `0`. | ||
|
|
||
| **Example 1:** | ||
|
|
||
| **Input:** differences = [1,-3,4], lower = 1, upper = 6 | ||
|
|
||
| **Output:** 2 | ||
|
|
||
| **Explanation:** The possible hidden sequences are: | ||
|
|
||
| - [3, 4, 1, 5] | ||
|
|
||
| - [4, 5, 2, 6] | ||
|
|
||
| Thus, we return 2. | ||
|
|
||
| **Example 2:** | ||
|
|
||
| **Input:** differences = [3,-4,5,1,-2], lower = -4, upper = 5 | ||
|
|
||
| **Output:** 4 | ||
|
|
||
| **Explanation:** The possible hidden sequences are: | ||
|
|
||
| - [-3, 0, -4, 1, 2, 0] | ||
|
|
||
| - [-2, 1, -3, 2, 3, 1] | ||
|
|
||
| - [-1, 2, -2, 3, 4, 2] | ||
|
|
||
| - [0, 3, -1, 4, 5, 3] | ||
|
|
||
| Thus, we return 4. | ||
|
|
||
| **Example 3:** | ||
|
|
||
| **Input:** differences = [4,-7,2], lower = 3, upper = 6 | ||
|
|
||
| **Output:** 0 | ||
|
|
||
| **Explanation:** There are no possible hidden sequences. Thus, we return 0. | ||
|
|
||
| **Constraints:** | ||
|
|
||
| * `n == differences.length` | ||
| * <code>1 <= n <= 10<sup>5</sup></code> | ||
| * <code>-10<sup>5</sup> <= differences[i] <= 10<sup>5</sup></code> | ||
| * <code>-10<sup>5</sup> <= lower <= upper <= 10<sup>5</sup></code> |
89 changes: 89 additions & 0 deletions
89
src/main/java/g2101_2200/s2146_k_highest_ranked_items_within_a_price_range/Solution.java
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,89 @@ | ||
| package g2101_2200.s2146_k_highest_ranked_items_within_a_price_range; | ||
|
|
||
| // #Medium #Array #Sorting #Breadth_First_Search #Matrix #Heap_Priority_Queue | ||
| // #2022_06_07_Time_81_ms_(88.84%)_Space_65.7_MB_(99.30%) | ||
|
|
||
| import java.util.Arrays; | ||
| import java.util.LinkedList; | ||
| import java.util.List; | ||
| import java.util.Queue; | ||
|
|
||
| public class Solution { | ||
| static class Item { | ||
| int row; | ||
| int col; | ||
| int dist; | ||
| int price; | ||
|
|
||
| public Item(int row, int col, int dist, int price) { | ||
| this.row = row; | ||
| this.col = col; | ||
| this.dist = dist; | ||
| this.price = price; | ||
| } | ||
| } | ||
|
|
||
| public List<List<Integer>> highestRankedKItems( | ||
| int[][] grid, int[] pricing, int[] start, int k) { | ||
| int n = grid.length; | ||
| int m = grid[0].length; | ||
| Queue<int[]> bfs = new LinkedList<>(); | ||
| LinkedList<Item> items = new LinkedList<>(); | ||
|
|
||
| bfs.add(start); | ||
| if (grid[start[0]][start[1]] >= pricing[0] && grid[start[0]][start[1]] <= pricing[1]) { | ||
| items.add(new Item(start[0], start[1], 0, grid[start[0]][start[1]])); | ||
| } | ||
| grid[start[0]][start[1]] = -1; | ||
|
|
||
| int distance = 0; | ||
| while (!bfs.isEmpty()) { | ||
| int size = bfs.size(); | ||
| distance++; | ||
| while (size-- > 0) { | ||
| int[] loc = bfs.poll(); | ||
| int[] dirX = {0, 1, -1, 0}; | ||
| int[] dirY = {-1, 0, 0, 1}; | ||
| for (int i = 0; i < 4; i++) { | ||
| int newX = loc[0] + dirX[i]; | ||
| int newY = loc[1] + dirY[i]; | ||
| if (newX < 0 | ||
| || newX >= n | ||
| || newY < 0 | ||
| || newY >= m | ||
| || grid[newX][newY] == -1 | ||
| || grid[newX][newY] == 0) { | ||
| continue; | ||
| } | ||
| if (grid[newX][newY] >= pricing[0] && grid[newX][newY] <= pricing[1]) { | ||
| items.add(new Item(newX, newY, distance, grid[newX][newY])); | ||
| } | ||
| grid[newX][newY] = -1; | ||
| bfs.add(new int[] {newX, newY}); | ||
| } | ||
| } | ||
| } | ||
| items.sort( | ||
| (a, b) -> { | ||
| int distDiff = a.dist - b.dist; | ||
| if (distDiff == 0) { | ||
| int priceDiff = a.price - b.price; | ||
| if (priceDiff == 0) { | ||
| int rowDiff = a.row - b.row; | ||
| if (rowDiff == 0) { | ||
| return a.col - b.col; | ||
| } | ||
| return rowDiff; | ||
| } | ||
| return priceDiff; | ||
| } | ||
| return distDiff; | ||
| }); | ||
| List<List<Integer>> ans = new LinkedList<>(); | ||
| while (k-- > 0 && !items.isEmpty()) { | ||
| Item item = items.poll(); | ||
| ans.add(Arrays.asList(item.row, item.col)); | ||
| } | ||
| return ans; | ||
| } | ||
| } |
107 changes: 107 additions & 0 deletions
107
...ain/java/g2101_2200/s2146_k_highest_ranked_items_within_a_price_range/readme.md
This file contains hidden or bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,107 @@ | ||
| 2146\. K Highest Ranked Items Within a Price Range | ||
|
|
||
| Medium | ||
|
|
||
| You are given a **0-indexed** 2D integer array `grid` of size `m x n` that represents a map of the items in a shop. The integers in the grid represent the following: | ||
|
|
||
| * `0` represents a wall that you cannot pass through. | ||
| * `1` represents an empty cell that you can freely move to and from. | ||
| * All other positive integers represent the price of an item in that cell. You may also freely move to and from these item cells. | ||
|
|
||
| It takes `1` step to travel between adjacent grid cells. | ||
|
|
||
| You are also given integer arrays `pricing` and `start` where `pricing = [low, high]` and `start = [row, col]` indicates that you start at the position `(row, col)` and are interested only in items with a price in the range of `[low, high]` (**inclusive**). You are further given an integer `k`. | ||
|
|
||
| You are interested in the **positions** of the `k` **highest-ranked** items whose prices are **within** the given price range. The rank is determined by the **first** of these criteria that is different: | ||
|
|
||
| 1. Distance, defined as the length of the shortest path from the `start` (**shorter** distance has a higher rank). | ||
| 2. Price (**lower** price has a higher rank, but it must be **in the price range**). | ||
| 3. The row number (**smaller** row number has a higher rank). | ||
| 4. The column number (**smaller** column number has a higher rank). | ||
|
|
||
| Return _the_ `k` _highest-ranked items within the price range **sorted** by their rank (highest to lowest)_. If there are fewer than `k` reachable items within the price range, return _**all** of them_. | ||
|
|
||
| **Example 1:** | ||
|
|
||
|  | ||
|
|
||
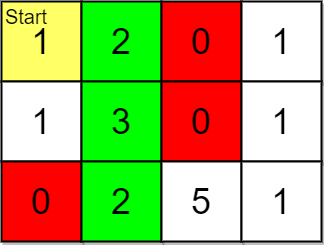
| **Input:** grid = [[1,2,0,1],[1,3,0,1],[0,2,5,1]], pricing = [2,5], start = [0,0], k = 3 | ||
|
|
||
| **Output:** [[0,1],[1,1],[2,1]] | ||
|
|
||
| **Explanation:** You start at (0,0). | ||
|
|
||
| With a price range of [2,5], we can take items from (0,1), (1,1), (2,1) and (2,2). | ||
|
|
||
| The ranks of these items are: | ||
|
|
||
| - (0,1) with distance 1 | ||
|
|
||
| - (1,1) with distance 2 | ||
|
|
||
| - (2,1) with distance 3 | ||
|
|
||
| - (2,2) with distance 4 | ||
|
|
||
| Thus, the 3 highest ranked items in the price range are (0,1), (1,1), and (2,1). | ||
|
|
||
| **Example 2:** | ||
|
|
||
| 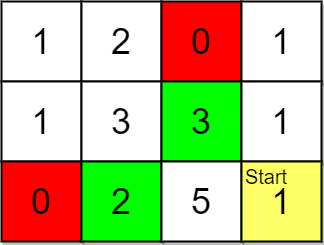 | ||
|
|
||
| **Input:** grid = [[1,2,0,1],[1,3,3,1],[0,2,5,1]], pricing = [2,3], start = [2,3], k = 2 | ||
|
|
||
| **Output:** [[2,1],[1,2]] | ||
|
|
||
| **Explanation:** You start at (2,3). | ||
|
|
||
| With a price range of [2,3], we can take items from (0,1), (1,1), (1,2) and (2,1). | ||
|
|
||
| The ranks of these items are: | ||
|
|
||
| - (2,1) with distance 2, price 2 | ||
|
|
||
| - (1,2) with distance 2, price 3 | ||
|
|
||
| - (1,1) with distance 3 | ||
|
|
||
| - (0,1) with distance 4 | ||
|
|
||
| Thus, the 2 highest ranked items in the price range are (2,1) and (1,2). | ||
|
|
||
| **Example 3:** | ||
|
|
||
| 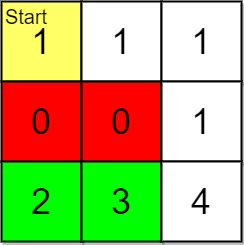 | ||
|
|
||
| **Input:** grid = [[1,1,1],[0,0,1],[2,3,4]], pricing = [2,3], start = [0,0], k = 3 | ||
|
|
||
| **Output:** [[2,1],[2,0]] | ||
|
|
||
| **Explanation:** You start at (0,0). | ||
|
|
||
| With a price range of [2,3], we can take items from (2,0) and (2,1). | ||
|
|
||
| The ranks of these items are: | ||
|
|
||
| - (2,1) with distance 5 | ||
|
|
||
| - (2,0) with distance 6 | ||
|
|
||
| Thus, the 2 highest ranked items in the price range are (2,1) and (2,0). | ||
|
|
||
| Note that k = 3 but there are only 2 reachable items within the price range. | ||
|
|
||
| **Constraints:** | ||
|
|
||
| * `m == grid.length` | ||
| * `n == grid[i].length` | ||
| * <code>1 <= m, n <= 10<sup>5</sup></code> | ||
| * <code>1 <= m * n <= 10<sup>5</sup></code> | ||
| * <code>0 <= grid[i][j] <= 10<sup>5</sup></code> | ||
| * `pricing.length == 2` | ||
| * <code>2 <= low <= high <= 10<sup>5</sup></code> | ||
| * `start.length == 2` | ||
| * `0 <= row <= m - 1` | ||
| * `0 <= col <= n - 1` | ||
| * `grid[row][col] > 0` | ||
| * `1 <= k <= m * n` |
Oops, something went wrong.
Add this suggestion to a batch that can be applied as a single commit.
This suggestion is invalid because no changes were made to the code.
Suggestions cannot be applied while the pull request is closed.
Suggestions cannot be applied while viewing a subset of changes.
Only one suggestion per line can be applied in a batch.
Add this suggestion to a batch that can be applied as a single commit.
Applying suggestions on deleted lines is not supported.
You must change the existing code in this line in order to create a valid suggestion.
Outdated suggestions cannot be applied.
This suggestion has been applied or marked resolved.
Suggestions cannot be applied from pending reviews.
Suggestions cannot be applied on multi-line comments.
Suggestions cannot be applied while the pull request is queued to merge.
Suggestion cannot be applied right now. Please check back later.
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Please add tags and public.