| comments | difficulty | edit_url |
|---|---|---|
true |
困难 |
「力扣挑战赛」中有一个由 N 个关卡组成的环形闯关游戏,关卡编号为 0~N-1,编号 0 的关卡和编号 N-1 的关卡相邻。每个关卡均有积分要求,challenge[i] 表示挑战编号 i 的关卡最少需要拥有的积分。
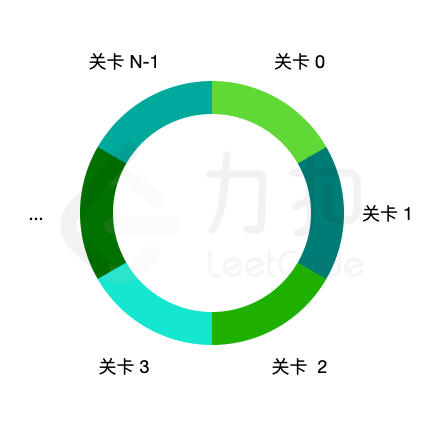
小扣想要挑战关卡,闯关具体规则如下:
- 初始小扣可以指定其中一个关卡为「开启」状态,其余关卡将处于「未开启」状态。
- 小扣可以挑战处于「开启」状态且满足最少积分要求的关卡,若小扣挑战该关卡前积分为
score,挑战结束后,积分将增长为score|challenge[i](即位运算中的"OR"运算) - 在挑战某个关卡后,该关卡两侧相邻的关卡将会开启(若之前未开启)
请帮助小扣进行计算,初始最少需要多少积分,可以挑战 环形闯关游戏 的所有关卡。
示例 1:
输入:
challenge = [5,4,6,2,7]输出:
4解释: 初始选择编号 3 的关卡开启,积分为 4 挑战编号 3 的关卡,积分变为
,开启 2、4 处的关卡 挑战编号 2 的关卡,积分变为 ,开启 1 处的关卡 挑战编号 1 的关卡,积分变为 ,开启 0 处的关卡 挑战编号 0 的关卡,积分变为 挑战编号 4 的关卡,顺利完成全部的关卡
示例 2:
输入:
challenge = [12,7,11,3,9]输出:
8解释: 初始选择编号 3 的关卡开启,积分为 8 挑战编号 3 的关卡,积分变为
,开启 2、4 处的关卡 挑战编号 2 的关卡,积分变为 ,开启 1 处的关卡 挑战编号 4 的关卡,积分变为 ,开启 0 处的关卡 挑战编号 1 的关卡,积分变为 挑战编号 0 的关卡,顺利完成全部的关卡
示例 3:
输入:
challenge = [1,1,1]输出:
1
提示:
1 <= challenge.length <= 5*10^41 <= challenge[i] <= 10^14