README_EN.md

96. Unique Binary Search Trees

中文文档

Description

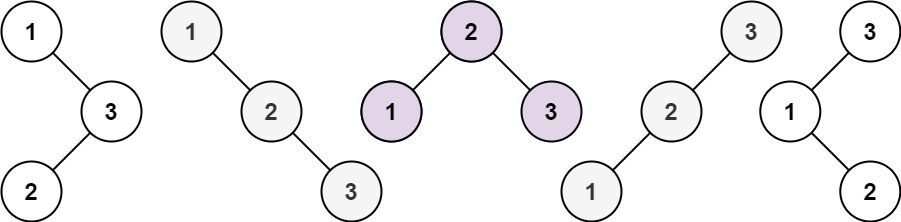
Given an integer n, return the number of structurally unique BST's (binary search trees) which has exactly n nodes of unique values from 1 to n.

 

Example 1:

Input: n = 3
Output: 5

Example 2:

Input: n = 1
Output: 1

 

Constraints:

• 1 <= n <= 19

Solutions

Solution 1: Dynamic Programming

We define $f[i]$ to represent the number of binary search trees that can be generated from $[1, i]$. Initially, $f[0] = 1$, and the answer is $f[n]$.

We can enumerate the number of nodes $i$, then the number of nodes in the left subtree $j \in [0, i - 1]$, and the number of nodes in the right subtree $k = i - j - 1$. The number of combinations of the number of nodes in the left subtree and the right subtree is $f[j] \times f[k]$, so $f[i] = \sum_{j = 0}^{i - 1} f[j] \times f[i - j - 1]$.

Finally, return $f[n]$.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes.

Python3

class Solution:
    def numTrees(self, n: int) -> int:
        f = [1] + [0] * n
        for i in range(n + 1):
            for j in range(i):
                f[i] += f[j] * f[i - j - 1]
        return f[n]

Java

class Solution {
    public int numTrees(int n) {
        int[] f = new int[n + 1];
        f[0] = 1;
        for (int i = 1; i <= n; ++i) {
            for (int j = 0; j < i; ++j) {
                f[i] += f[j] * f[i - j - 1];
            }
        }
        return f[n];
    }
}

C++

class Solution {
public:
    int numTrees(int n) {
        vector<int> f(n + 1);
        f[0] = 1;
        for (int i = 1; i <= n; ++i) {
            for (int j = 0; j < i; ++j) {
                f[i] += f[j] * f[i - j - 1];
            }
        }
        return f[n];
    }
};

Go

func numTrees(n int) int {
	f := make([]int, n+1)
	f[0] = 1
	for i := 1; i <= n; i++ {
		for j := 0; j < i; j++ {
			f[i] += f[j] * f[i-j-1]
		}
	}
	return f[n]
}

Rust

impl Solution {
    pub fn num_trees(n: i32) -> i32 {
        let n = n as usize;
        let mut f = vec![0; n + 1];
        f[0] = 1;
        for i in 1..=n {
            for j in 0..i {
                f[i] += f[j] * f[i - j - 1];
            }
        }
        f[n] as i32
    }
}

TypeScript

function numTrees(n: number): number {
    const f: number[] = Array(n + 1).fill(0);
    f[0] = 1;
    for (let i = 1; i <= n; ++i) {
        for (let j = 0; j < i; ++j) {
            f[i] += f[j] * f[i - j - 1];
        }
    }
    return f[n];
}

C#

public class Solution {
    public int NumTrees(int n) {
        int[] f = new int[n + 1];
        f[0] = 1;
        for (int i = 1; i <= n; ++i) {
            for (int j = 0; j < i; ++j) {
                f[i] += f[j] * f[i - j - 1];
            }
        }
        return f[n];
    }
}

...