README.md

894. 所有可能的真二叉树

English Version

题目描述

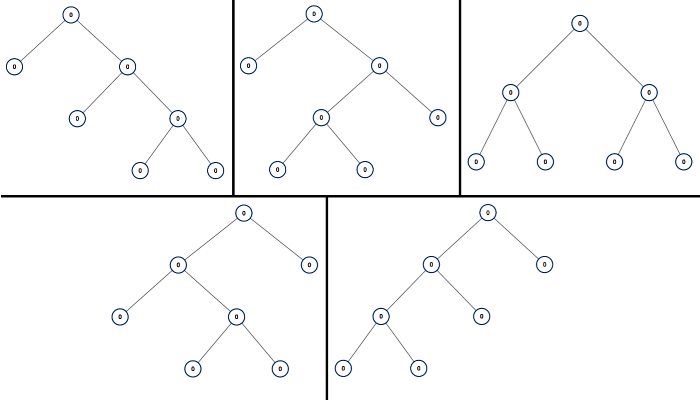
给你一个整数 n ，请你找出所有可能含 n 个节点的 真二叉树 ，并以列表形式返回。答案中每棵树的每个节点都必须符合 Node.val == 0 。

答案的每个元素都是一棵真二叉树的根节点。你可以按 任意顺序 返回最终的真二叉树列表。

真二叉树 是一类二叉树，树中每个节点恰好有 0 或 2 个子节点。

 

示例 1：

输入：n = 7
输出：[[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]

示例 2：

输入：n = 3
输出：[[0,0,0]]

 

提示：

• 1 <= n <= 20

解法

方法一：记忆化搜索

对于 $n=1$，直接返回单个节点的列表。

对于 $n>1$，若 $n$ 为奇数，按照左右子树遍历不同的排列组合，得到结果列表；若 $n$ 为偶数，返回空列表。

此过程可以用记忆化搜索，避免重复计算。

时间复杂度 $O(2^n)$，空间复杂度 $O(2^n)$。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:
        @cache
        def dfs(n):
            if n == 1:
                return [TreeNode()]
            res = []
            if n % 2:
                for i in range(n - 1):
                    j = n - i - 1
                    for left in dfs(i):
                        for right in dfs(j):
                            res.append(TreeNode(0, left, right))
            return res

        return dfs(n)

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private List<TreeNode>[] f = new List[21];

    public List<TreeNode> allPossibleFBT(int n) {
        return dfs(n);
    }

    private List<TreeNode> dfs(int n) {
        if (f[n] != null) {
            return f[n];
        }
        if (n == 1) {
            return Collections.singletonList(new TreeNode());
        }
        List<TreeNode> res = new ArrayList<>();
        for (int i = 0; i < n - 1; ++i) {
            int j = n - i - 1;
            for (TreeNode left : dfs(i)) {
                for (TreeNode right : dfs(j)) {
                    res.add(new TreeNode(0, left, right));
                }
            }
        }
        f[n] = res;
        return res;
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<TreeNode*> allPossibleFBT(int n) {
        vector<TreeNode*> f[21];
        function<vector<TreeNode*>(int)> dfs = [&](int n) -> vector<TreeNode*> {
            if (f[n].size()) return f[n];
            if (n == 1) return vector<TreeNode*>{new TreeNode()};
            vector<TreeNode*> res;
            for (int i = 0; i < n - 1; ++i) {
                int j = n - i - 1;
                for (auto left : dfs(i)) {
                    for (auto right : dfs(j)) {
                        res.push_back(new TreeNode(0, left, right));
                    }
                }
            }
            return f[n] = res;
        };
        return dfs(n);
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func allPossibleFBT(n int) []*TreeNode {
	f := map[int][]*TreeNode{}
	var dfs func(n int) []*TreeNode
	dfs = func(n int) []*TreeNode {
		if v, ok := f[n]; ok {
			return v
		}
		if n == 1 {
			return []*TreeNode{&TreeNode{Val: 0}}
		}
		res := []*TreeNode{}
		for i := 0; i < n-1; i++ {
			j := n - i - 1
			for _, left := range dfs(i) {
				for _, right := range dfs(j) {
					res = append(res, &TreeNode{0, left, right})
				}
			}
		}
		f[n] = res
		return res
	}
	return dfs(n)
}

...