README.md

3027. 人员站位的方案数 II

English Version

题目描述

给你一个  n x 2 的二维数组 points ，它表示二维平面上的一些点坐标，其中 points[i] = [xi, yi] 。

我们定义 x 轴的正方向为 右 （x 轴递增的方向），x 轴的负方向为 左 （x 轴递减的方向）。类似的，我们定义 y 轴的正方向为 上 （y 轴递增的方向），y 轴的负方向为 下 （y 轴递减的方向）。

你需要安排这 n 个人的站位，这 n 个人中包括 liupengsay 和小羊肖恩 。你需要确保每个点处 恰好 有 一个 人。同时，liupengsay 想跟小羊肖恩单独玩耍，所以 liupengsay 会以 liupengsay 的坐标为 左上角 ，小羊肖恩的坐标为 右下角 建立一个矩形的围栏（注意，围栏可能 不 包含任何区域，也就是说围栏可能是一条线段）。如果围栏的 内部 或者 边缘 上有任何其他人，liupengsay 都会难过。

请你在确保 liupengsay 不会 难过的前提下，返回 liupengsay 和小羊肖恩可以选择的 点对 数目。

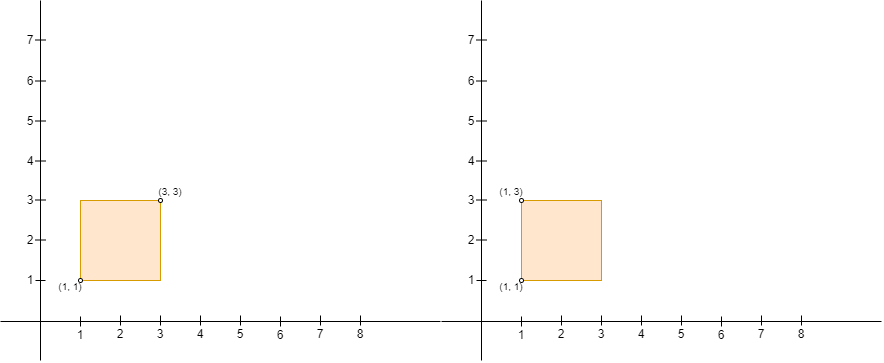
注意，liupengsay 建立的围栏必须确保 liupengsay 的位置是矩形的左上角，小羊肖恩的位置是矩形的右下角。比方说，以 (1, 1) ，(1, 3) ，(3, 1) 和 (3, 3) 为矩形的四个角，给定下图的两个输入，liupengsay 都不能建立围栏，原因如下：

• 图一中，liupengsay 在 (3, 3) 且小羊肖恩在 (1, 1) ，liupengsay 的位置不是左上角且小羊肖恩的位置不是右下角。
• 图二中，liupengsay 在 (1, 3) 且小羊肖恩在 (1, 1) ，小羊肖恩的位置不是在围栏的右下角。

 

示例 1：

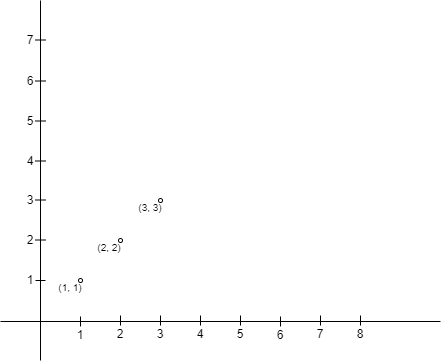
输入：points = [[1,1],[2,2],[3,3]]
输出：0
解释：没有办法可以让 liupengsay 的围栏以 liupengsay 的位置为左上角且小羊肖恩的位置为右下角。所以我们返回 0 。

示例 2：

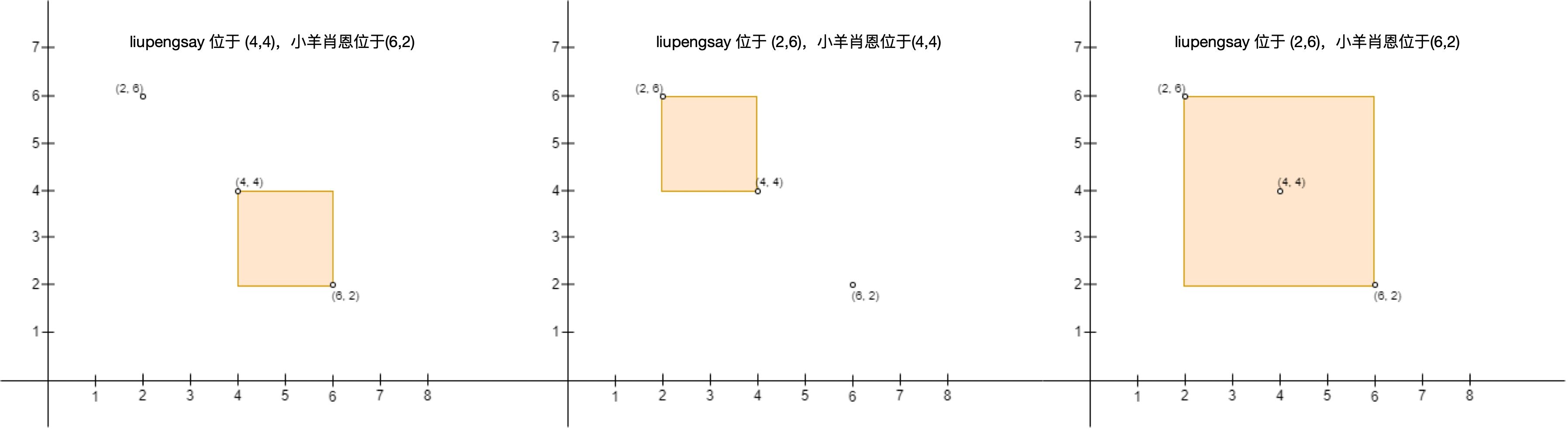
输入：points = [[6,2],[4,4],[2,6]]
输出：2
解释：总共有 2 种方案安排 liupengsay 和小羊肖恩的位置，使得 liupengsay 不会难过：
- liupengsay 站在 (4, 4) ，小羊肖恩站在 (6, 2) 。
- liupengsay 站在 (2, 6) ，小羊肖恩站在 (4, 4) 。
不能安排 liupengsay 站在 (2, 6) 且小羊肖恩站在 (6, 2) ，因为站在 (4, 4) 的人处于围栏内。

示例 3：

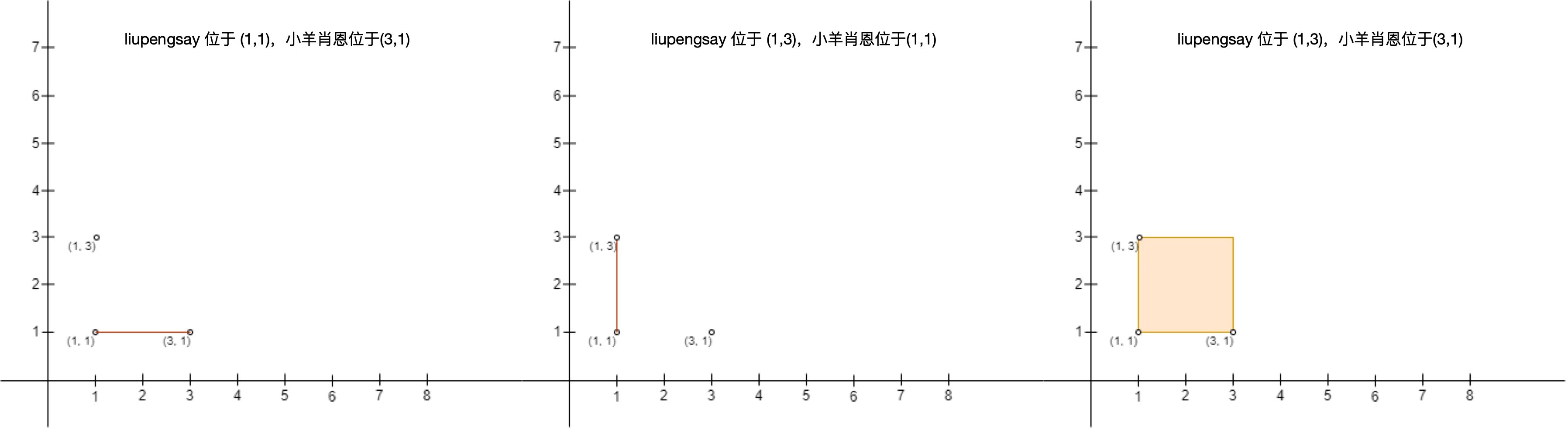
输入：points = [[3,1],[1,3],[1,1]]
输出：2
解释：总共有 2 种方案安排 liupengsay 和小羊肖恩的位置，使得 liupengsay 不会难过：
- liupengsay 站在 (1, 1) ，小羊肖恩站在 (3, 1) 。
- liupengsay 站在 (1, 3) ，小羊肖恩站在 (1, 1) 。
不能安排 liupengsay 站在 (1, 3) 且小羊肖恩站在 (3, 1) ，因为站在 (1, 1) 的人处于围栏内。
注意围栏是可以不包含任何面积的，上图中第一和第二个围栏都是合法的。

 

提示：

• 2 <= n <= 1000
• points[i].length == 2
• -109 <= points[i][0], points[i][1] <= 109
• points[i] 点对两两不同。

解法

方法一：排序 + 枚举

我们不妨考虑枚举矩形左上角的点 $(x_1,y_1)$，那么根据题目，右下角的点 $(x_2,y_2)$ 随着 $x$ 的增大，纵坐标 $y$ 也会要严格增大，才符合题意。

因此，我们对所有点按照 $x$ 坐标升序排序，如果 $x$ 坐标相同，按照 $y$ 坐标降序排序。

然后我们枚举左上角的点 $(x_1,y_1)$，并且维护一个最大的 $y_2$，记为 $maxY$，表示所有右下角的点的纵坐标的最大值。然后我们枚举右下角的点 $(x_2,y_2)$，如果 $y_2$ 大于 $maxY$ 并且小于等于 $y_1$，那么我们就找到了一个合法的方案，将答案加一，然后更新 $maxY$ 为 $y_2$。

枚举完所有的点对后，我们就得到了答案。

时间复杂度 $O(n^2)$，空间复杂度 $O(\log n)$。其中 $n$ 是点的数量。

class Solution:
    def numberOfPairs(self, points: List[List[int]]) -> int:
        points.sort(key=lambda x: (x[0], -x[1]))
        ans = 0
        for i, (_, y1) in enumerate(points):
            max_y = -inf
            for _, y2 in points[i + 1 :]:
                if max_y < y2 <= y1:
                    max_y = y2
                    ans += 1
        return ans

class Solution {
    public int numberOfPairs(int[][] points) {
        Arrays.sort(points, (a, b) -> a[0] == b[0] ? b[1] - a[1] : a[0] - b[0]);
        int ans = 0;
        int n = points.length;
        final int inf = 1 << 30;
        for (int i = 0; i < n; ++i) {
            int y1 = points[i][1];
            int maxY = -inf;
            for (int j = i + 1; j < n; ++j) {
                int y2 = points[j][1];
                if (maxY < y2 && y2 <= y1) {
                    maxY = y2;
                    ++ans;
                }
            }
        }
        return ans;
    }
}

class Solution {
public:
    int numberOfPairs(vector<vector<int>>& points) {
        sort(points.begin(), points.end(), [](const vector<int>& a, const vector<int>& b) {
            return a[0] < b[0] || (a[0] == b[0] && b[1] < a[1]);
        });
        int n = points.size();
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            int y1 = points[i][1];
            int maxY = INT_MIN;
            for (int j = i + 1; j < n; ++j) {
                int y2 = points[j][1];
                if (maxY < y2 && y2 <= y1) {
                    maxY = y2;
                    ++ans;
                }
            }
        }
        return ans;
    }
};

func numberOfPairs(points [][]int) (ans int) {
	sort.Slice(points, func(i, j int) bool {
		return points[i][0] < points[j][0] || points[i][0] == points[j][0] && points[j][1] < points[i][1]
	})
	for i, p1 := range points {
		y1 := p1[1]
		maxY := math.MinInt32
		for _, p2 := range points[i+1:] {
			y2 := p2[1]
			if maxY < y2 && y2 <= y1 {
				maxY = y2
				ans++
			}
		}
	}
	return
}

function numberOfPairs(points: number[][]): number {
    points.sort((a, b) => (a[0] === b[0] ? b[1] - a[1] : a[0] - b[0]));
    const n = points.length;
    let ans = 0;
    for (let i = 0; i < n; ++i) {
        const [_, y1] = points[i];
        let maxY = -Infinity;
        for (let j = i + 1; j < n; ++j) {
            const [_, y2] = points[j];
            if (maxY < y2 && y2 <= y1) {
                maxY = y2;
                ++ans;
            }
        }
    }
    return ans;
}

public class Solution {
    public int NumberOfPairs(int[][] points) {
        Array.Sort(points, (a, b) => a[0] == b[0] ? b[1] - a[1] : a[0] - b[0]);
        int ans = 0;
        int n = points.Length;
        int inf = 1 << 30;
        for (int i = 0; i < n; ++i) {
            int y1 = points[i][1];
            int maxY = -inf;
            for (int j = i + 1; j < n; ++j) {
                int y2 = points[j][1];
                if (maxY < y2 && y2 <= y1) {
                    maxY = y2;
                    ++ans;
                }
            }
        }
        return ans;
    }
}