README.md

802. 找到最终的安全状态

English Version

题目描述

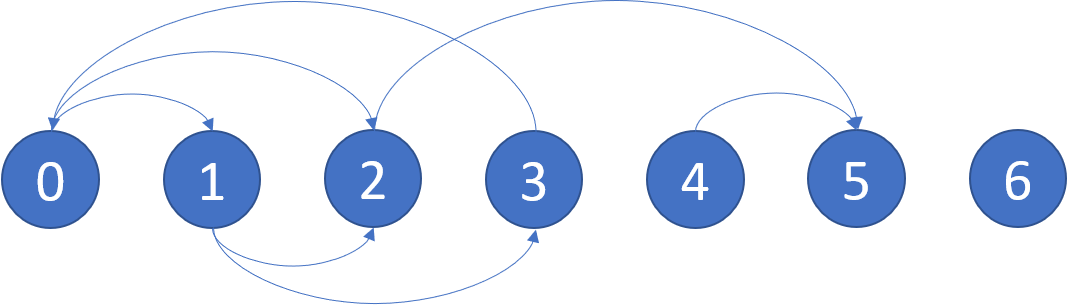
在有向图中，从某个节点和每个转向处开始出发，沿着图的有向边走。如果到达的节点是终点（即它没有连出的有向边），则停止。

如果从起始节点出发，最后必然能走到终点，就认为起始节点是 最终安全 的。更具体地说，对于最终安全的起始节点而言，存在一个自然数 k ，无论选择沿哪条有向边行走 ，走了不到 k 步后必能停止在一个终点上。

返回一个由图中所有最终安全的起始节点组成的数组作为答案。答案数组中的元素应当按 升序 排列。

该有向图有 n 个节点，按 0 到 n - 1 编号，其中 n 是 graph 的节点数。图以下述形式给出：graph[i] 是编号 j 节点的一个列表，满足 (i, j) 是图的一条有向边。

 

示例 1：

输入：graph = [[1,2],[2,3],[5],[0],[5],[],[]]
输出：[2,4,5,6]
解释：示意图如上。

示例 2：

输入：graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]]
输出：[4]

 

提示：

• n == graph.length
• 1 <= n <= 104
• 0 <= graph[i].legnth <= n
• graph[i] 按严格递增顺序排列。
• 图中可能包含自环。
• 图中边的数目在范围 [1, 4 * 104] 内。

解法

出度为零的点是安全的，如果一个点只能到达安全的点，那么它同样是安全的，所以问题转换成了拓扑排序。

Python3

class Solution:
    def eventualSafeNodes(self, graph: List[List[int]]) -> List[int]:
        n = len(graph)
        outDegree = [len(vs) for vs in graph]
        revGraph = [[] for _ in range(n)]
        for u, vs in enumerate(graph):
            for v in vs:
                revGraph[v].append(u)
        q = deque([i for i, d in enumerate(outDegree) if d == 0])
        while q:
            for u in revGraph[q.popleft()]:
                outDegree[u] -= 1
                if outDegree[u] == 0:
                    q.append(u)
        return [i for i, d in enumerate(outDegree) if d == 0]

Java

class Solution {
    public List<Integer> eventualSafeNodes(int[][] graph) {
        int n = graph.length;
        int[] outDegrees = new int[n];
        Queue<Integer> queue = new ArrayDeque<>();
        List<List<Integer>> revGraph = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            revGraph.add(new ArrayList<>());
        }
        for (int u = 0; u < n; u++) {
            for (int v : graph[u]) {
                revGraph.get(v).add(u);
            }
            outDegrees[u] = graph[u].length;
            if (outDegrees[u] == 0) {
                queue.offer(u);
            }
        }

        while (!queue.isEmpty()) {
            int v = queue.poll();
            for (int u : revGraph.get(v)) {
                if (--outDegrees[u] == 0) {
                    queue.offer(u);
                }
            }
        }

        List<Integer> ans = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            if (outDegrees[i] == 0) {
                ans.add(i);
            }
        }
        return ans;
    }
}

Go

func eventualSafeNodes(graph [][]int) []int {
	n := len(graph)
	outDegree := make([]int, n)
	revGraph := make([][]int, n)
	queue := make([]int, 0)
	ans := make([]int, 0)

	for u, vs := range graph {
		for _, v := range vs {
			revGraph[v] = append(revGraph[v], u)
		}
		outDegree[u] = len(vs)
		if outDegree[u] == 0 {
			queue = append(queue, u)
		}
	}

	for len(queue) > 0 {
		v := queue[0]
		queue = queue[1:]
		for _, u := range revGraph[v] {
			outDegree[u]--
			if outDegree[u] == 0 {
				queue = append(queue, u)
			}
		}
	}

	for i, d := range outDegree {
		if d == 0 {
			ans = append(ans, i)
		}
	}
	return ans
}

C++

class Solution {
public:
    vector<int> eventualSafeNodes(vector<vector<int>> &graph) {
        int n = graph.size();
        vector<vector<int>> revGraph(n);
        vector<int> outDegree(n);
        for (int i = 0; i < n; ++i)
        {
            outDegree[i] += graph[i].size();
            for (int j : graph[i])
                revGraph[j].push_back(i);
        }
        queue<int> q;
        for (int i = 0; i < n; ++i)
            if (outDegree[i] == 0)
                q.push(i);
        while (!q.empty())
        {
            int i = q.front();
            q.pop();
            for (int j : revGraph[i])
            {
                if (--outDegree[j] == 0)
                    q.push(j);
            }
        }
        vector<int> ans;
        for (int i = 0; i < n; ++i)
            if (outDegree[i] == 0)
                ans.push_back(i);
        return ans;
    }
};

...