You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
Example usage below. Note that `ModelingToolkit` does not force unit conversions to preferred units in the event of nonstandard combinations -- it merely checks that the equations are consistent.
An example of an inconsistent system: at present, `ModelingToolkit` requires that the units of all terms in an equation or sum to be equal-valued (`ModelingToolkit.equivalent(u1,u2)`), rather that simply dimensionally consistent. In the future, the validation stage may be upgraded to support the insertion of conversion factors into the equations.
# parameter `τ` can be assigned a value, but constant `h` cannot
28
28
sol = solve(prob)
29
+
30
+
using Plots
29
31
plot(sol)
30
32
```
31
-
32
-
33
33
Now let's start digging into MTK!
34
34
35
35
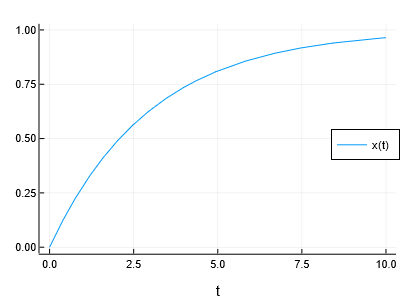
## Your very first ODE
@@ -46,7 +46,7 @@ variable, ``f(t)`` is an external forcing function, and ``\tau`` is a
46
46
parameter. In MTK, this system can be modelled as follows. For simplicity, we
47
47
first set the forcing function to a time-independent value.
48
48
49
-
```julia
49
+
```@example ode2
50
50
using ModelingToolkit
51
51
52
52
@variables t x(t) # independent and dependent variables
@@ -56,11 +56,6 @@ D = Differential(t) # define an operator for the differentiation w.r.t. time
56
56
57
57
# your first ODE, consisting of a single equation, indicated by ~
58
58
@named fol_model = ODESystem(D(x) ~ (h - x)/τ)
59
-
# Model fol_model with 1 equations
60
-
# States (1):
61
-
# x(t)
62
-
# Parameters (1):
63
-
# τ
64
59
```
65
60
66
61
Note that equations in MTK use the tilde character (`~`) as equality sign.
@@ -69,16 +64,14 @@ matches the name in the REPL. If omitted, you can directly set the `name` keywor
69
64
70
65
After construction of the ODE, you can solve it using [DifferentialEquations.jl](https://docs.sciml.ai/DiffEqDocs/stable/):
@@ -140,8 +125,6 @@ when using `parameters` (e.g., solution of linear equations by dividing out
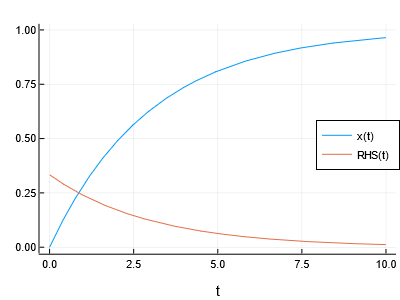
140
125
the constant's value, which cannot be done for parameters, since they may
141
126
be zero).
142
127
143
-
144
-
145
128
Note that the indexing of the solution similarly works via the names, and so
146
129
`sol[x]` gives the time-series for `x`, `sol[x,2:10]` gives the 2nd through 10th
147
130
values of `x` matching `sol.t`, etc. Note that this works even for variables
@@ -152,7 +135,7 @@ which have been eliminated, and thus `sol[RHS]` retrieves the values of `RHS`.
152
135
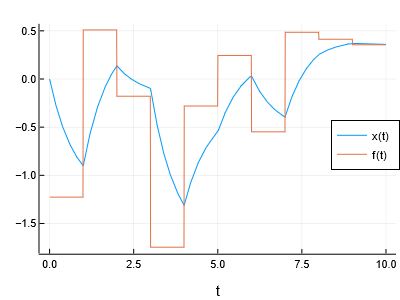
What if the forcing function (the “external input”) ``f(t)`` is not constant?
153
136
Obviously, one could use an explicit, symbolic function of time:
@@ -166,7 +149,7 @@ So, you could, for example, interpolate given the time-series using
166
149
we illustrate this option by a simple lookup ("zero-order hold") of a vector
167
150
of random values:
168
151
169
-
```julia
152
+
```@example ode2
170
153
value_vector = randn(10)
171
154
f_fun(t) = t >= 10 ? value_vector[end] : value_vector[Int(floor(t))+1]
172
155
@register_symbolic f_fun(t)
@@ -178,15 +161,13 @@ sol = solve(prob)
178
161
plot(sol, vars=[x,f])
179
162
```
180
163
181
-
182
-
183
164
## Building component-based, hierarchical models
184
165
185
166
Working with simple one-equation systems is already fun, but composing more
186
167
complex systems from simple ones is even more fun. Best practice for such a
187
168
“modeling framework” could be to use factory functions for model components:
188
169
189
-
```julia
170
+
```@example ode2
190
171
function fol_factory(separate=false;name)
191
172
@parameters τ
192
173
@variables t x(t) f(t) RHS(t)
@@ -202,7 +183,7 @@ end
202
183
Such a factory can then be used to instantiate the same component multiple times,
203
184
but allows for customization:
204
185
205
-
```julia
186
+
```@example ode2
206
187
@named fol_1 = fol_factory()
207
188
@named fol_2 = fol_factory(true) # has observable RHS
208
189
```
@@ -212,21 +193,11 @@ Now, these two components can be used as subsystems of a parent system, i.e.
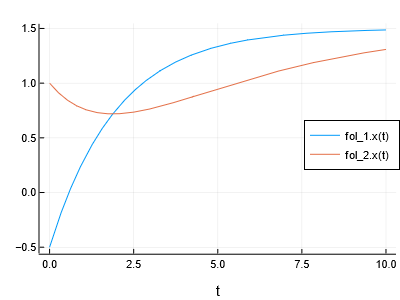
212
193
one level higher in the model hierarchy. The connections between the components
279
-
280
235
More on this topic may be found in [Composing Models and Building Reusable Components](@ref acausal).
281
236
282
237
## Defaults
283
238
284
239
It is often a good idea to specify reasonable values for the initial state and the
285
240
parameters of a model component. Then, these do not have to be explicitly specified when constructing the `ODEProblem`.
286
241
287
-
```julia
242
+
```@example ode2
288
243
function unitstep_fol_factory(;name)
289
244
@parameters τ
290
245
@variables t x(t)
@@ -311,21 +266,25 @@ By default, analytical derivatives and sparse matrices, e.g. for the Jacobian, t
311
266
matrix of first partial derivatives, are not used. Let's benchmark this (`prob`
312
267
still is the problem using the `connected_simp` system above):
313
268
314
-
```julia
269
+
```@example ode2
315
270
using BenchmarkTools
316
-
317
-
@btimesolve($prob, Rodas4());
318
-
# 251.300 μs (873 allocations: 31.18 KiB)
271
+
@btime solve(prob, Rodas4());
272
+
nothing # hide
319
273
```
320
274
321
275
Now have MTK provide sparse, analytical derivatives to the solver. This has to
322
276
be specified during the construction of the `ODEProblem`:
0 commit comments