|
| 1 | +# Automated Index Reduction of DAEs via ModelingToolkitize |
| 2 | + |
| 3 | +In many cases one may accidentally write down a DAE that is not easily solvable |
| 4 | +by numerical methods. In this tutorial we will walk through an example of a |
| 5 | +pendulum which accidentally generates an index-3 DAE, and show how to use the |
| 6 | +`modelingtoolkitize` to correct the model definition before solving. |
| 7 | + |
| 8 | +## Copy-Pastable Example |
| 9 | + |
| 10 | +```julia |
| 11 | +using ModelingToolkit |
| 12 | +using LinearAlgebra |
| 13 | +using OrdinaryDiffEq |
| 14 | +using Plots |
| 15 | + |
| 16 | +function pendulum!(du, u, p, t) |
| 17 | + x, dx, y, dy, T = u |
| 18 | + g, L = p |
| 19 | + du[1] = dx |
| 20 | + du[2] = T*x |
| 21 | + du[3] = dy |
| 22 | + du[4] = T*y - g |
| 23 | + du[5] = x^2 + y^2 - L^2 |
| 24 | + return nothing |
| 25 | +end |
| 26 | +pendulum_fun! = ODEFunction(pendulum!, mass_matrix=Diagonal([1,1,1,1,0])) |
| 27 | +u0 = [1.0, 0, 0, 0, 0] |
| 28 | +p = [9.8, 1] |
| 29 | +tspan = (0, 10.0) |
| 30 | +pendulum_prob = ODEProblem(pendulum_fun!, u0, tspan, p) |
| 31 | +traced_sys = modelingtoolkitize(pendulum_prob) |
| 32 | +pendulum_sys = structural_simplify(dae_index_lowering(traced_sys)) |
| 33 | +prob = ODAEProblem(pendulum_sys, Pair[], tspan) |
| 34 | +sol = solve(prob, Tsit5(),abstol=1e-8,reltol=1e-8) |
| 35 | +plot(sol, vars=states(traced_sys)) |
| 36 | +``` |
| 37 | + |
| 38 | +## Explanation |
| 39 | + |
| 40 | +### Attempting to Solve the Equation |
| 41 | + |
| 42 | +In this tutorial we will look at the pendulum system: |
| 43 | + |
| 44 | +```math |
| 45 | +\begin{align} |
| 46 | + x^\prime &= v_x\\ |
| 47 | + v_x^\prime &= Tx\\ |
| 48 | + y^\prime &= v_y\\ |
| 49 | + v_y^\prime &= Ty - g\\ |
| 50 | + 0 &= x^2 + y^2 - L^2 |
| 51 | +\end{align} |
| 52 | +``` |
| 53 | + |
| 54 | +As a good DifferentialEquations.jl user, one would follow |
| 55 | +[the mass matrix DAE tutorial](https://diffeq.sciml.ai/stable/tutorials/advanced_ode_example/#Handling-Mass-Matrices) |
| 56 | +to arrive at code for simulating the model: |
| 57 | + |
| 58 | +```julia |
| 59 | +using OrdinaryDiffEq, LinearAlgebra |
| 60 | +function pendulum!(du, u, p, t) |
| 61 | + x, dx, y, dy, T = u |
| 62 | + g, L = p |
| 63 | + du[1] = dx; du[2] = T*x |
| 64 | + du[3] = dy; du[4] = T*y - g |
| 65 | + du[5] = x^2 + y^2 - L^2 |
| 66 | +end |
| 67 | +pendulum_fun! = ODEFunction(pendulum!, mass_matrix=Diagonal([1,1,1,1,0])) |
| 68 | +u0 = [1.0, 0, 0, 0, 0]; p = [9.8, 1]; tspan = (0, 10.0) |
| 69 | +pendulum_prob = ODEProblem(pendulum_fun!, u0, tspan, p) |
| 70 | +solve(pendulum_prob,Rodas4()) |
| 71 | +``` |
| 72 | + |
| 73 | +However, one will quickly be greeted with the unfortunate message: |
| 74 | + |
| 75 | +```julia |
| 76 | +┌ Warning: First function call produced NaNs. Exiting. |
| 77 | +└ @ OrdinaryDiffEq C:\Users\accou\.julia\packages\OrdinaryDiffEq\yCczp\src\initdt.jl:76 |
| 78 | +┌ Warning: Automatic dt set the starting dt as NaN, causing instability. |
| 79 | +└ @ OrdinaryDiffEq C:\Users\accou\.julia\packages\OrdinaryDiffEq\yCczp\src\solve.jl:485 |
| 80 | +┌ Warning: NaN dt detected. Likely a NaN value in the state, parameters, or derivative value caused this outcome. |
| 81 | +└ @ SciMLBase C:\Users\accou\.julia\packages\SciMLBase\DrPil\src\integrator_interface.jl:325 |
| 82 | +``` |
| 83 | + |
| 84 | +Did you implement the DAE incorrectly? No. Is the solver broken? No. |
| 85 | + |
| 86 | +### Understanding DAE Index |
| 87 | + |
| 88 | +It turns out that this is a property of the DAE that we are attempting to solve. |
| 89 | +This kind of DAE is known as an index-3 DAE. For a complete discussion of DAE |
| 90 | +index, see [this article](http://www.scholarpedia.org/article/Differential-algebraic_equations). |
| 91 | +Essentially the issue here is that we have 4 differential variables (``x``, ``v_x``, ``y``, ``v_y``) |
| 92 | +and one algebraic variable ``T`` (which we can know because there is no `D(T)` |
| 93 | +term in the equations). An index-1 DAE always satisfies that the Jacobian of |
| 94 | +the algebraic equations is non-singular. Here, the first 4 equations are |
| 95 | +differential equations, with the last term the algebraic relationship. However, |
| 96 | +the partial derivative of `x^2 + y^2 - L^2` w.r.t. `T` is zero, and thus the |
| 97 | +Jacobian of the algebraic equations is the zero matrix and thus it's singular. |
| 98 | +This is a very quick way to see whether the DAE is index 1! |
| 99 | + |
| 100 | +The problem with higher order DAEs is that the matrices used in Newton solves |
| 101 | +are singular or close to singular when applied to such problems. Because of this |
| 102 | +fact, the nonlinear solvers (or Rosenbrock methods) break down, making them |
| 103 | +difficult to solve. The classic paper [DAEs are not ODEs](https://epubs.siam.org/doi/10.1137/0903023) |
| 104 | +goes into detail on this and shows that many methods are no longer convergent |
| 105 | +when index is higher than one. So it's not necessarily the fault of the solver |
| 106 | +or the implementation: this is known. |
| 107 | + |
| 108 | +But that's not a satisfying answer, so what do you do about it? |
| 109 | + |
| 110 | +### Transforming Higher Order DAEs to Index-1 DAEs |
| 111 | + |
| 112 | +It turns out that higher order DAEs can be transformed into lower order DAEs. |
| 113 | +If you differentiate the last equation two times and perform a substitution, |
| 114 | +you can arrive at the following set of equations: |
| 115 | + |
| 116 | +```math |
| 117 | +\begin{align} |
| 118 | +x^\prime =& v_x \\ |
| 119 | +v_x^\prime =& x T \\ |
| 120 | +y^\prime =& v_y \\ |
| 121 | +v_y^\prime =& y T - g \\ |
| 122 | +0 =& 2 \left(v_x^{2} + v_y^{2} + y ( y T - g ) + T x^2 \right) |
| 123 | +\end{align} |
| 124 | +``` |
| 125 | + |
| 126 | +Note that this is mathematically-equivalent to the equation that we had before, |
| 127 | +but the Jacobian w.r.t. `T` of the algebraic equation is no longer zero because |
| 128 | +of the substitution. This means that if you wrote down this version of the model |
| 129 | +it will be index-1 and solve correctly! In fact, this is how DAE index is |
| 130 | +commonly defined: the number of differentiations it takes to transform the DAE |
| 131 | +into an ODE, where an ODE is an index-0 DAE by substituting out all of the |
| 132 | +algebraic relationships. |
| 133 | + |
| 134 | +### Automating the Index Reduction |
| 135 | + |
| 136 | +However, requiring the user to sit there and work through this process on |
| 137 | +potentially millions of equations is an unfathomable mental overhead. But, |
| 138 | +we can avoid this by using methods like |
| 139 | +[the Pantelides algorithm](https://ptolemy.berkeley.edu/projects/embedded/eecsx44/lectures/Spring2013/modelica-dae-part-2.pdf) |
| 140 | +for automatically performing this reduction to index 1. While this requires the |
| 141 | +ModelingToolkit symbolic form, we use `modelingtoolkitize` to transform |
| 142 | +the numerical code into symbolic code, run `dae_index_lowering` lowering, |
| 143 | +then transform back to numerical code with `ODEProblem`, and solve with a |
| 144 | +numerical solver. Let's try that out: |
| 145 | + |
| 146 | +```julia |
| 147 | +traced_sys = modelingtoolkitize(pendulum_prob) |
| 148 | +pendulum_sys = structural_simplify(dae_index_lowering(traced_sys)) |
| 149 | +prob = ODEProblem(pendulum_sys, Pair[], tspan) |
| 150 | +sol = solve(prob, Rodas4()) |
| 151 | + |
| 152 | +using Plots |
| 153 | +plot(sol, vars=states(traced_sys)) |
| 154 | +``` |
| 155 | + |
| 156 | +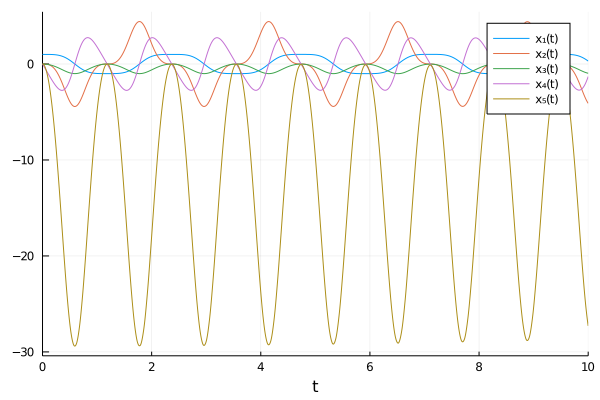 |
| 157 | + |
| 158 | +Note that plotting using `states(traced_sys)` is done so that any |
| 159 | +variables which are symbolically eliminated, or any variable reorderings |
| 160 | +done for enhanced parallelism/performance, still show up in the resulting |
| 161 | +plot and the plot is shown in the same order as the original numerical |
| 162 | +code. |
| 163 | + |
| 164 | +Note that we can even go a little bit further. If we use the `ODAEProblem` |
| 165 | +constructor, we can remove the algebraic equations from the states of the |
| 166 | +system and fully transform the index-3 DAE into an index-0 ODE which can |
| 167 | +be solved via an explicit Runge-Kutta method: |
| 168 | + |
| 169 | +```julia |
| 170 | +traced_sys = modelingtoolkitize(pendulum_prob) |
| 171 | +pendulum_sys = structural_simplify(dae_index_lowering(traced_sys)) |
| 172 | +prob = ODAEProblem(pendulum_sys, Pair[], tspan) |
| 173 | +sol = solve(prob, Tsit5(),abstol=1e-8,reltol=1e-8) |
| 174 | +plot(sol, vars=states(traced_sys)) |
| 175 | +``` |
| 176 | + |
| 177 | +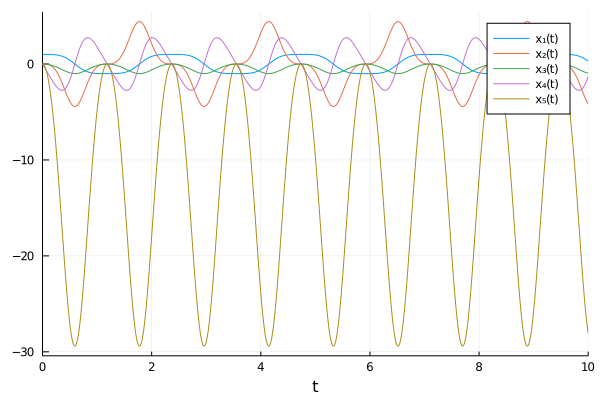 |
| 178 | + |
| 179 | +And there you go: this has transformed the model from being too hard to |
| 180 | +solve with implicit DAE solvers, to something that is easily solved with |
| 181 | +explicit Runge-Kutta methods for non-stiff equations. |
0 commit comments