comments	difficulty	edit_url	rating	source	tags
true	中等	https://github.com/doocs/leetcode/edit/main/solution/2000-2099/2002.Maximum%20Product%20of%20the%20Length%20of%20Two%20Palindromic%20Subsequences/README.md	1869	第 258 场周赛 Q3	位运算 字符串 动态规划 回溯 状态压缩

2002. 两个回文子序列长度的最大乘积

English Version

题目描述

给你一个字符串 s ，请你找到 s 中两个 不相交回文子序列 ，使得它们长度的 乘积最大 。两个子序列在原字符串中如果没有任何相同下标的字符，则它们是 不相交 的。

请你返回两个回文子序列长度可以达到的 最大乘积 。

子序列 指的是从原字符串中删除若干个字符（可以一个也不删除）后，剩余字符不改变顺序而得到的结果。如果一个字符串从前往后读和从后往前读一模一样，那么这个字符串是一个 回文字符串 。

 

示例 1：

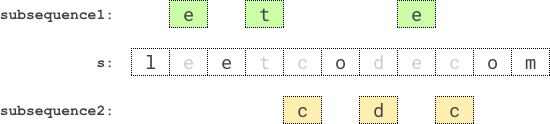
输入：s = "leetcodecom"
输出：9
解释：最优方案是选择 "ete" 作为第一个子序列，"cdc" 作为第二个子序列。
它们的乘积为 3 * 3 = 9 。

示例 2：

输入：s = "bb"
输出：1
解释：最优方案为选择 "b" （第一个字符）作为第一个子序列，"b" （第二个字符）作为第二个子序列。
它们的乘积为 1 * 1 = 1 。

示例 3：

输入：s = "accbcaxxcxx"
输出：25
解释：最优方案为选择 "accca" 作为第一个子序列，"xxcxx" 作为第二个子序列。
它们的乘积为 5 * 5 = 25 。

 

提示：

• 2 <= s.length <= 12
• s 只含有小写英文字母。

解法

方法一：二进制枚举

我们注意到，字符串 $s$ 的长度不超过 $12$，因此我们可以使用二进制枚举的方法来枚举 $s$ 的所有子序列。不妨设 $s$ 的长度为 $n$，我们可以使用 $2^n$ 个长度为 $n$ 的二进制数来表示 $s$ 的所有子序列。对于每个二进制数，第 $i$ 位为 $1$ 表示 $s$ 的第 $i$ 个字符在子序列中，为 $0$ 表示不在子序列中。我们对于每个二进制数，判断其是否为回文子序列，并且记录在数组 $p$ 中。

接下来，我们枚举 $p$ 中的每个数 $i$，如果 $i$ 是回文子序列，那么我们可以从 $i$ 的补集 $mx = (2^n - 1) \oplus i$ 中枚举一个数 $j$，如果 $j$ 也是回文子序列，那么 $i$ 和 $j$ 就是我们要找的两个回文子序列，它们的长度分别为 $i$ 和 $j$ 的二进制表示中的 $1$ 的个数，我们记为 $a$ 和 $b$，那么它们的乘积就是 $a \times b$，我们取所有可能的 $a \times b$ 中的最大值即可。

时间复杂度 $(2^n \times n + 3^n)$，空间复杂度 $O(2^n)$。其中 $n$ 为字符串 $s$ 的长度。

Python3

class Solution:
    def maxProduct(self, s: str) -> int:
        n = len(s)
        p = [True] * (1 << n)
        for k in range(1, 1 << n):
            i, j = 0, n - 1
            while i < j:
                while i < j and (k >> i & 1) == 0:
                    i += 1
                while i < j and (k >> j & 1) == 0:
                    j -= 1
                if i < j and s[i] != s[j]:
                    p[k] = False
                    break
                i, j = i + 1, j - 1
        ans = 0
        for i in range(1, 1 << n):
            if p[i]:
                mx = ((1 << n) - 1) ^ i
                j = mx
                a = i.bit_count()
                while j:
                    if p[j]:
                        b = j.bit_count()
                        ans = max(ans, a * b)
                    j = (j - 1) & mx
        return ans

Java

class Solution {
    public int maxProduct(String s) {
        int n = s.length();
        boolean[] p = new boolean[1 << n];
        Arrays.fill(p, true);
        for (int k = 1; k < 1 << n; ++k) {
            for (int i = 0, j = n - 1; i < n; ++i, --j) {
                while (i < j && (k >> i & 1) == 0) {
                    ++i;
                }
                while (i < j && (k >> j & 1) == 0) {
                    --j;
                }
                if (i < j && s.charAt(i) != s.charAt(j)) {
                    p[k] = false;
                    break;
                }
            }
        }
        int ans = 0;
        for (int i = 1; i < 1 << n; ++i) {
            if (p[i]) {
                int a = Integer.bitCount(i);
                int mx = ((1 << n) - 1) ^ i;
                for (int j = mx; j > 0; j = (j - 1) & mx) {
                    if (p[j]) {
                        int b = Integer.bitCount(j);
                        ans = Math.max(ans, a * b);
                    }
                }
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int maxProduct(string s) {
        int n = s.size();
        vector<bool> p(1 << n, true);
        for (int k = 1; k < 1 << n; ++k) {
            for (int i = 0, j = n - 1; i < j; ++i, --j) {
                while (i < j && !(k >> i & 1)) {
                    ++i;
                }
                while (i < j && !(k >> j & 1)) {
                    --j;
                }
                if (i < j && s[i] != s[j]) {
                    p[k] = false;
                    break;
                }
            }
        }
        int ans = 0;
        for (int i = 1; i < 1 << n; ++i) {
            if (p[i]) {
                int a = __builtin_popcount(i);
                int mx = ((1 << n) - 1) ^ i;
                for (int j = mx; j; j = (j - 1) & mx) {
                    if (p[j]) {
                        int b = __builtin_popcount(j);
                        ans = max(ans, a * b);
                    }
                }
            }
        }
        return ans;
    }
};

Go

func maxProduct(s string) (ans int) {
	n := len(s)
	p := make([]bool, 1<<n)
	for i := range p {
		p[i] = true
	}
	for k := 1; k < 1<<n; k++ {
		for i, j := 0, n-1; i < j; i, j = i+1, j-1 {
			for i < j && (k>>i&1) == 0 {
				i++
			}
			for i < j && (k>>j&1) == 0 {
				j--
			}
			if i < j && s[i] != s[j] {
				p[k] = false
				break
			}
		}
	}
	for i := 1; i < 1<<n; i++ {
		if p[i] {
			a := bits.OnesCount(uint(i))
			mx := (1<<n - 1) ^ i
			for j := mx; j > 0; j = (j - 1) & mx {
				if p[j] {
					b := bits.OnesCount(uint(j))
					ans = max(ans, a*b)
				}
			}
		}
	}
	return

}