| comments | difficulty | edit_url |
|---|---|---|
true |
中等 |
欢迎各位勇者来到力扣城,本次试炼主题为「二叉搜索树染色」。
每位勇士面前设有一个二叉搜索树的模型,模型的根节点为 root,树上的各个节点值均不重复。初始时,所有节点均为蓝色。现在按顺序对这棵二叉树进行若干次操作, ops[i] = [type, x, y] 表示第 i 次操作为:
type等于 0 时,将节点值范围在[x, y]的节点均染蓝type等于 1 时,将节点值范围在[x, y]的节点均染红
请返回完成所有染色后,该二叉树中红色节点的数量。
注意:
- 题目保证对于每个操作的
x、y值定出现在二叉搜索树节点中
示例 1:
输入:
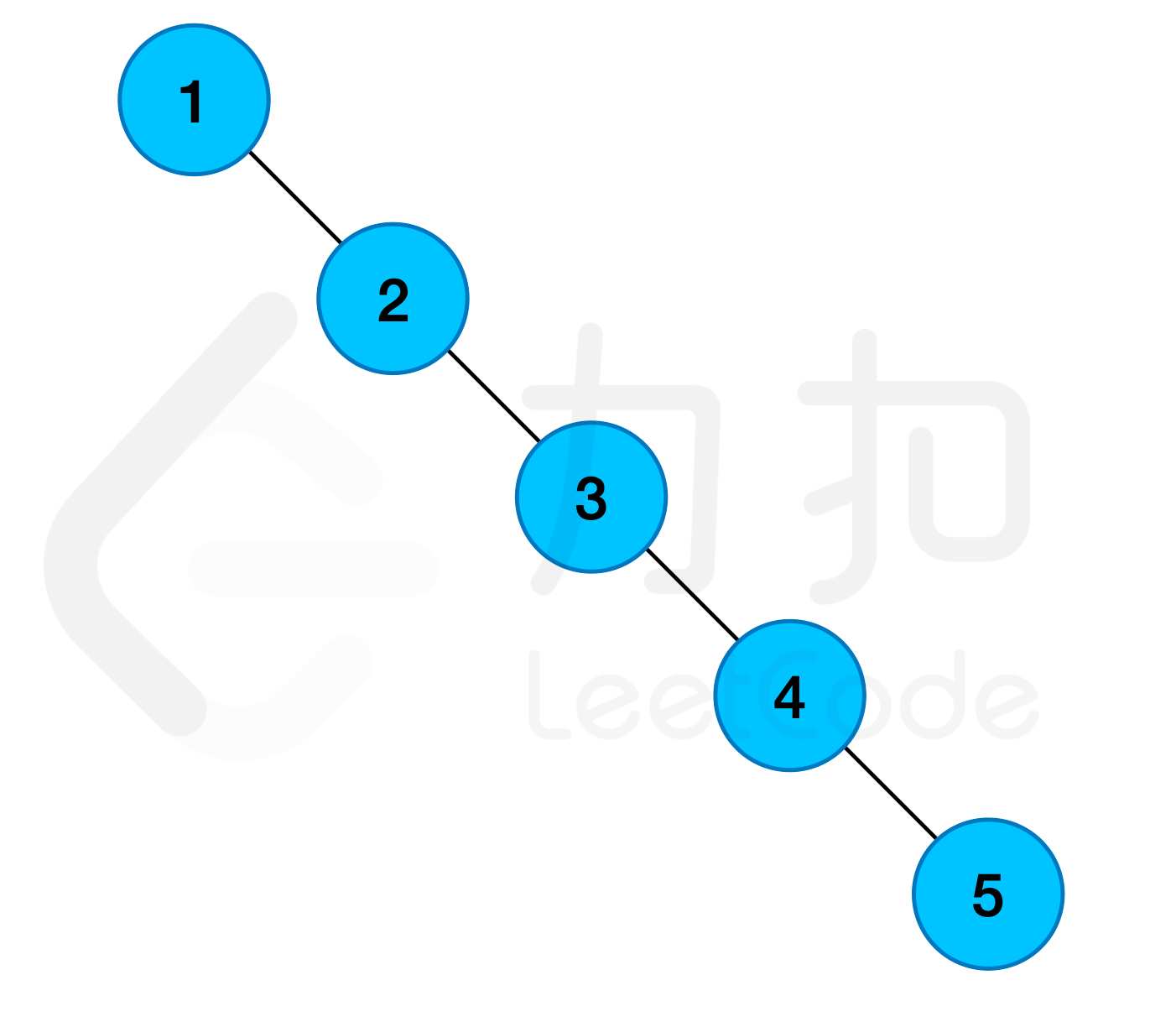
root = [1,null,2,null,3,null,4,null,5], ops = [[1,2,4],[1,1,3],[0,3,5]]输出:
2解释: 第 0 次操作,将值为 2、3、4 的节点染红; 第 1 次操作,将值为 1、2、3 的节点染红; 第 2 次操作,将值为 3、4、5 的节点染蓝; 因此,最终值为 1、2 的节点为红色节点,返回数量 2
{:width=230px}
示例 2:
输入:
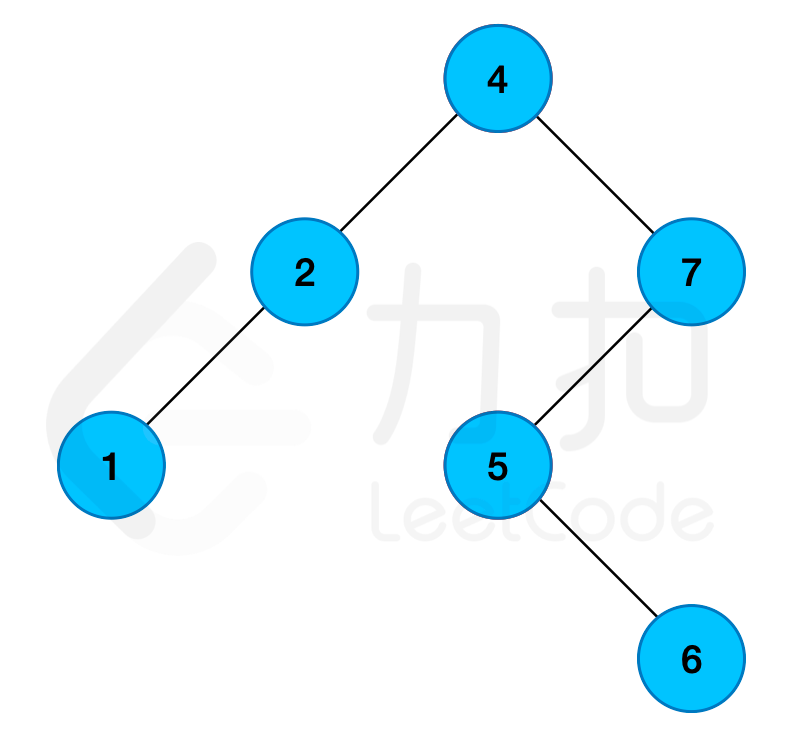
root = [4,2,7,1,null,5,null,null,null,null,6]>ops = [[0,2,2],[1,1,5],[0,4,5],[1,5,7]]输出:
5解释: 第 0 次操作,将值为 2 的节点染蓝; 第 1 次操作,将值为 1、2、4、5 的节点染红; 第 2 次操作,将值为 4、5 的节点染蓝; 第 3 次操作,将值为 5、6、7 的节点染红; 因此,最终值为 1、2、5、6、7 的节点为红色节点,返回数量 5
{:width=230px}
提示:
1 <= 二叉树节点数量 <= 10^51 <= ops.length <= 10^5ops[i].length == 3ops[i][0]仅为0or10 <= ops[i][1] <= ops[i][2] <= 10^90 <= 节点值 <= 10^9
我们先遍历一遍二叉树,将所有节点的值加入到有序集合中。
接下来,由于节点的染色状态只跟最后一个操作有关,因此,我们可以倒序遍历操作数组。对于每个操作
最后,我们返回答案。
时间复杂度
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
from sortedcontainers import SortedList
class Solution:
def getNumber(self, root: Optional[TreeNode], ops: List[List[int]]) -> int:
def dfs(root):
if root is None:
return
sl.add(root.val)
dfs(root.left)
dfs(root.right)
sl = SortedList()
dfs(root)
ans = 0
for t, x, y in ops[::-1]:
i = sl.bisect_left(x)
while i < len(sl) and sl[i] <= y:
sl.pop(i)
ans += t == 1
return ans/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
private TreeSet<Integer> ts = new TreeSet<>();
public int getNumber(TreeNode root, int[][] ops) {
dfs(root);
int ans = 0;
for (int i = ops.length - 1; i >= 0; --i) {
int t = ops[i][0];
int x = ops[i][1], y = ops[i][2];
Integer ceiling = ts.ceiling(x);
while (ceiling != null && ceiling <= y) {
ts.remove(ceiling);
ceiling = ts.ceiling(x);
ans += t;
}
}
return ans;
}
private void dfs(TreeNode root) {
if (root == null) {
return;
}
ts.add(root.val);
dfs(root.left);
dfs(root.right);
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int getNumber(TreeNode* root, vector<vector<int>>& ops) {
set<int> ts;
function<void(TreeNode*)> dfs = [&](TreeNode* root) {
if (root == nullptr) {
return;
}
ts.insert(root->val);
dfs(root->left);
dfs(root->right);
};
dfs(root);
int ans = 0;
for (int i = ops.size() - 1; ~i; --i) {
int t = ops[i][0];
int x = ops[i][1], y = ops[i][2];
auto it = ts.lower_bound(x);
while (it != ts.end() && *it <= y) {
ts.erase(it++);
ans += t;
}
}
return ans;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func getNumber(root *TreeNode, ops [][]int) (ans int) {
rbt := redblacktree.NewWithIntComparator()
var dfs func(root *TreeNode)
dfs = func(root *TreeNode) {
if root == nil {
return
}
rbt.Put(root.Val, nil)
dfs(root.Left)
dfs(root.Right)
}
dfs(root)
for i := len(ops) - 1; i >= 0; i-- {
t, x, y := ops[i][0], ops[i][1], ops[i][2]
node, _ := rbt.Ceiling(x)
for node != nil && node.Key.(int) <= y {
rbt.Remove(node.Key)
node, _ = rbt.Ceiling(x)
ans += t
}
}
return
}/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function getNumber(root: TreeNode | null, ops: number[][]): number {
const ts = new TreeSet<number>();
const dfs = (node: TreeNode | null) => {
if (!node) {
return;
}
ts.add(node.val);
dfs(node.left);
dfs(node.right);
};
dfs(root);
let ans = 0;
for (let i = ops.length - 1; ~i; --i) {
const [t, x, y] = ops[i];
let ceiling = ts.ceil(x);
while (ceiling !== null && ceiling <= y) {
ts.delete(ceiling);
ceiling = ts.ceil(x);
ans += t;
}
}
return ans;
}
type Compare<T> = (lhs: T, rhs: T) => number;
class RBTreeNode<T = number> {
data: T;
count: number;
left: RBTreeNode<T> | null;
right: RBTreeNode<T> | null;
parent: RBTreeNode<T> | null;
color: number;
constructor(data: T) {
this.data = data;
this.left = this.right = this.parent = null;
this.color = 0;
this.count = 1;
}
sibling(): RBTreeNode<T> | null {
if (!this.parent) return null; // sibling null if no parent
return this.isOnLeft() ? this.parent.right : this.parent.left;
}
isOnLeft(): boolean {
return this === this.parent!.left;
}
hasRedChild(): boolean {
return (
Boolean(this.left && this.left.color === 0) ||
Boolean(this.right && this.right.color === 0)
);
}
}
class RBTree<T> {
root: RBTreeNode<T> | null;
lt: (l: T, r: T) => boolean;
constructor(compare: Compare<T> = (l: T, r: T) => (l < r ? -1 : l > r ? 1 : 0)) {
this.root = null;
this.lt = (l: T, r: T) => compare(l, r) < 0;
}
rotateLeft(pt: RBTreeNode<T>): void {
const right = pt.right!;
pt.right = right.left;
if (pt.right) pt.right.parent = pt;
right.parent = pt.parent;
if (!pt.parent) this.root = right;
else if (pt === pt.parent.left) pt.parent.left = right;
else pt.parent.right = right;
right.left = pt;
pt.parent = right;
}
rotateRight(pt: RBTreeNode<T>): void {
const left = pt.left!;
pt.left = left.right;
if (pt.left) pt.left.parent = pt;
left.parent = pt.parent;
if (!pt.parent) this.root = left;
else if (pt === pt.parent.left) pt.parent.left = left;
else pt.parent.right = left;
left.right = pt;
pt.parent = left;
}
swapColor(p1: RBTreeNode<T>, p2: RBTreeNode<T>): void {
const tmp = p1.color;
p1.color = p2.color;
p2.color = tmp;
}
swapData(p1: RBTreeNode<T>, p2: RBTreeNode<T>): void {
const tmp = p1.data;
p1.data = p2.data;
p2.data = tmp;
}
fixAfterInsert(pt: RBTreeNode<T>): void {
let parent = null;
let grandParent = null;
while (pt !== this.root && pt.color !== 1 && pt.parent?.color === 0) {
parent = pt.parent;
grandParent = pt.parent.parent;
/* Case : A
Parent of pt is left child of Grand-parent of pt */
if (parent === grandParent?.left) {
const uncle = grandParent.right;
/* Case : 1
The uncle of pt is also red
Only Recoloring required */
if (uncle && uncle.color === 0) {
grandParent.color = 0;
parent.color = 1;
uncle.color = 1;
pt = grandParent;
} else {
/* Case : 2
pt is right child of its parent
Left-rotation required */
if (pt === parent.right) {
this.rotateLeft(parent);
pt = parent;
parent = pt.parent;
}
/* Case : 3
pt is left child of its parent
Right-rotation required */
this.rotateRight(grandParent);
this.swapColor(parent!, grandParent);
pt = parent!;
}
} else {
/* Case : B
Parent of pt is right child of Grand-parent of pt */
const uncle = grandParent!.left;
/* Case : 1
The uncle of pt is also red
Only Recoloring required */
if (uncle != null && uncle.color === 0) {
grandParent!.color = 0;
parent.color = 1;
uncle.color = 1;
pt = grandParent!;
} else {
/* Case : 2
pt is left child of its parent
Right-rotation required */
if (pt === parent.left) {
this.rotateRight(parent);
pt = parent;
parent = pt.parent;
}
/* Case : 3
pt is right child of its parent
Left-rotation required */
this.rotateLeft(grandParent!);
this.swapColor(parent!, grandParent!);
pt = parent!;
}
}
}
this.root!.color = 1;
}
delete(val: T): boolean {
const node = this.find(val);
if (!node) return false;
node.count--;
if (!node.count) this.deleteNode(node);
return true;
}
deleteAll(val: T): boolean {
const node = this.find(val);
if (!node) return false;
this.deleteNode(node);
return true;
}
deleteNode(v: RBTreeNode<T>): void {
const u = BSTreplace(v);
// True when u and v are both black
const uvBlack = (u === null || u.color === 1) && v.color === 1;
const parent = v.parent!;
if (!u) {
// u is null therefore v is leaf
if (v === this.root) this.root = null;
// v is root, making root null
else {
if (uvBlack) {
// u and v both black
// v is leaf, fix double black at v
this.fixDoubleBlack(v);
} else {
// u or v is red
if (v.sibling()) {
// sibling is not null, make it red"
v.sibling()!.color = 0;
}
}
// delete v from the tree
if (v.isOnLeft()) parent.left = null;
else parent.right = null;
}
return;
}
if (!v.left || !v.right) {
// v has 1 child
if (v === this.root) {
// v is root, assign the value of u to v, and delete u
v.data = u.data;
v.left = v.right = null;
} else {
// Detach v from tree and move u up
if (v.isOnLeft()) parent.left = u;
else parent.right = u;
u.parent = parent;
if (uvBlack) this.fixDoubleBlack(u);
// u and v both black, fix double black at u
else u.color = 1; // u or v red, color u black
}
return;
}
// v has 2 children, swap data with successor and recurse
this.swapData(u, v);
this.deleteNode(u);
// find node that replaces a deleted node in BST
function BSTreplace(x: RBTreeNode<T>): RBTreeNode<T> | null {
// when node have 2 children
if (x.left && x.right) return successor(x.right);
// when leaf
if (!x.left && !x.right) return null;
// when single child
return x.left ?? x.right;
}
// find node that do not have a left child
// in the subtree of the given node
function successor(x: RBTreeNode<T>): RBTreeNode<T> {
let temp = x;
while (temp.left) temp = temp.left;
return temp;
}
}
fixDoubleBlack(x: RBTreeNode<T>): void {
if (x === this.root) return; // Reached root
const sibling = x.sibling();
const parent = x.parent!;
if (!sibling) {
// No sibiling, double black pushed up
this.fixDoubleBlack(parent);
} else {
if (sibling.color === 0) {
// Sibling red
parent.color = 0;
sibling.color = 1;
if (sibling.isOnLeft()) this.rotateRight(parent);
// left case
else this.rotateLeft(parent); // right case
this.fixDoubleBlack(x);
} else {
// Sibling black
if (sibling.hasRedChild()) {
// at least 1 red children
if (sibling.left && sibling.left.color === 0) {
if (sibling.isOnLeft()) {
// left left
sibling.left.color = sibling.color;
sibling.color = parent.color;
this.rotateRight(parent);
} else {
// right left
sibling.left.color = parent.color;
this.rotateRight(sibling);
this.rotateLeft(parent);
}
} else {
if (sibling.isOnLeft()) {
// left right
sibling.right!.color = parent.color;
this.rotateLeft(sibling);
this.rotateRight(parent);
} else {
// right right
sibling.right!.color = sibling.color;
sibling.color = parent.color;
this.rotateLeft(parent);
}
}
parent.color = 1;
} else {
// 2 black children
sibling.color = 0;
if (parent.color === 1) this.fixDoubleBlack(parent);
else parent.color = 1;
}
}
}
}
insert(data: T): boolean {
// search for a position to insert
let parent = this.root;
while (parent) {
if (this.lt(data, parent.data)) {
if (!parent.left) break;
else parent = parent.left;
} else if (this.lt(parent.data, data)) {
if (!parent.right) break;
else parent = parent.right;
} else break;
}
// insert node into parent
const node = new RBTreeNode(data);
if (!parent) this.root = node;
else if (this.lt(node.data, parent.data)) parent.left = node;
else if (this.lt(parent.data, node.data)) parent.right = node;
else {
parent.count++;
return false;
}
node.parent = parent;
this.fixAfterInsert(node);
return true;
}
find(data: T): RBTreeNode<T> | null {
let p = this.root;
while (p) {
if (this.lt(data, p.data)) {
p = p.left;
} else if (this.lt(p.data, data)) {
p = p.right;
} else break;
}
return p ?? null;
}
*inOrder(root: RBTreeNode<T> = this.root!): Generator<T, undefined, void> {
if (!root) return;
for (const v of this.inOrder(root.left!)) yield v;
yield root.data;
for (const v of this.inOrder(root.right!)) yield v;
}
*reverseInOrder(root: RBTreeNode<T> = this.root!): Generator<T, undefined, void> {
if (!root) return;
for (const v of this.reverseInOrder(root.right!)) yield v;
yield root.data;
for (const v of this.reverseInOrder(root.left!)) yield v;
}
}
class TreeSet<T = number> {
_size: number;
tree: RBTree<T>;
compare: Compare<T>;
constructor(
collection: T[] | Compare<T> = [],
compare: Compare<T> = (l: T, r: T) => (l < r ? -1 : l > r ? 1 : 0),
) {
if (typeof collection === 'function') {
compare = collection;
collection = [];
}
this._size = 0;
this.compare = compare;
this.tree = new RBTree(compare);
for (const val of collection) this.add(val);
}
size(): number {
return this._size;
}
has(val: T): boolean {
return !!this.tree.find(val);
}
add(val: T): boolean {
const successful = this.tree.insert(val);
this._size += successful ? 1 : 0;
return successful;
}
delete(val: T): boolean {
const deleted = this.tree.deleteAll(val);
this._size -= deleted ? 1 : 0;
return deleted;
}
ceil(val: T): T | undefined {
let p = this.tree.root;
let higher = null;
while (p) {
if (this.compare(p.data, val) >= 0) {
higher = p;
p = p.left;
} else {
p = p.right;
}
}
return higher?.data;
}
floor(val: T): T | undefined {
let p = this.tree.root;
let lower = null;
while (p) {
if (this.compare(val, p.data) >= 0) {
lower = p;
p = p.right;
} else {
p = p.left;
}
}
return lower?.data;
}
higher(val: T): T | undefined {
let p = this.tree.root;
let higher = null;
while (p) {
if (this.compare(val, p.data) < 0) {
higher = p;
p = p.left;
} else {
p = p.right;
}
}
return higher?.data;
}
lower(val: T): T | undefined {
let p = this.tree.root;
let lower = null;
while (p) {
if (this.compare(p.data, val) < 0) {
lower = p;
p = p.right;
} else {
p = p.left;
}
}
return lower?.data;
}
first(): T | undefined {
return this.tree.inOrder().next().value;
}
last(): T | undefined {
return this.tree.reverseInOrder().next().value;
}
shift(): T | undefined {
const first = this.first();
if (first === undefined) return undefined;
this.delete(first);
return first;
}
pop(): T | undefined {
const last = this.last();
if (last === undefined) return undefined;
this.delete(last);
return last;
}
*[Symbol.iterator](): Generator<T, void, void> {
for (const val of this.values()) yield val;
}
*keys(): Generator<T, void, void> {
for (const val of this.values()) yield val;
}
*values(): Generator<T, undefined, void> {
for (const val of this.tree.inOrder()) yield val;
return undefined;
}
/**
* Return a generator for reverse order traversing the set
*/
*rvalues(): Generator<T, undefined, void> {
for (const val of this.tree.reverseInOrder()) yield val;
return undefined;
}
}