comments	difficulty	edit_url	rating	source	tags
true	困难	https://github.com/doocs/leetcode/edit/main/solution/1300-1399/1340.Jump%20Game%20V/README.md	1866	第 174 场周赛 Q4	数组 动态规划 排序

1340. 跳跃游戏 V

English Version

题目描述

给你一个整数数组 arr 和一个整数 d 。每一步你可以从下标 i 跳到：

• i + x ，其中 i + x < arr.length 且 0 < x <= d 。
• i - x ，其中 i - x >= 0 且 0 < x <= d 。

除此以外，你从下标 i 跳到下标 j 需要满足：arr[i] > arr[j] 且 arr[i] > arr[k] ，其中下标 k 是所有 i 到 j 之间的数字（更正式的，min(i, j) < k < max(i, j)）。

你可以选择数组的任意下标开始跳跃。请你返回你 最多 可以访问多少个下标。

请注意，任何时刻你都不能跳到数组的外面。

 

示例 1：

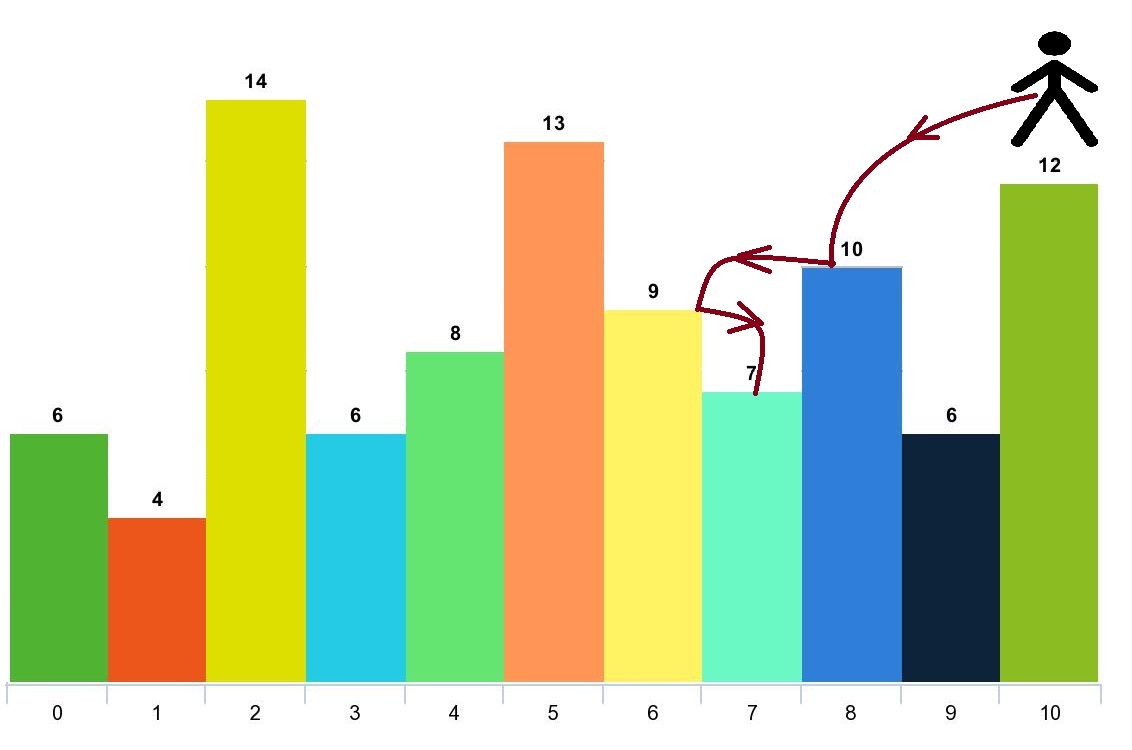
输入：arr = [6,4,14,6,8,13,9,7,10,6,12], d = 2
输出：4
解释：你可以从下标 10 出发，然后如上图依次经过 10 --> 8 --> 6 --> 7 。
注意，如果你从下标 6 开始，你只能跳到下标 7 处。你不能跳到下标 5 处因为 13 > 9 。你也不能跳到下标 4 处，因为下标 5 在下标 4 和 6 之间且 13 > 9 。
类似的，你不能从下标 3 处跳到下标 2 或者下标 1 处。

示例 2：

输入：arr = [3,3,3,3,3], d = 3
输出：1
解释：你可以从任意下标处开始且你永远无法跳到任何其他坐标。

示例 3：

输入：arr = [7,6,5,4,3,2,1], d = 1
输出：7
解释：从下标 0 处开始，你可以按照数值从大到小，访问所有的下标。

示例 4：

输入：arr = [7,1,7,1,7,1], d = 2
输出：2

示例 5：

输入：arr = [66], d = 1
输出：1

 

提示：

• 1 <= arr.length <= 1000
• 1 <= arr[i] <= 10^5
• 1 <= d <= arr.length

解法

方法一：记忆化搜索

我们设计一个函数 $dfs(i)$，表示从下标 $i$ 开始跳跃能够访问的最大下标数。我们可以枚举 $i$ 的所有合法的跳跃目标 $j$，即 $i-d\le j\le i+d$，并且 $arr[i]>arr[j]$。对于每个合法的 $j$，我们可以递归地计算 $dfs(j)$，并取其中的最大值。最终的答案即为所有 $i$ 的 $dfs(i)$ 的最大值。

我们可以使用记忆化搜索来优化这个过程，即使用一个数组 $f$ 记录每个下标的 $dfs$ 值，避免重复计算。

时间复杂度 $O(n\times d)$，空间复杂度 $O(n)$。其中 $n$ 为数组 $arr$ 的长度。

Python3

class Solution:
    def maxJumps(self, arr: List[int], d: int) -> int:
        @cache
        def dfs(i):
            ans = 1
            for j in range(i - 1, -1, -1):
                if i - j > d or arr[j] >= arr[i]:
                    break
                ans = max(ans, 1 + dfs(j))
            for j in range(i + 1, n):
                if j - i > d or arr[j] >= arr[i]:
                    break
                ans = max(ans, 1 + dfs(j))
            return ans

        n = len(arr)
        return max(dfs(i) for i in range(n))

Java

class Solution {
    private int n;
    private int d;
    private int[] arr;
    private Integer[] f;

    public int maxJumps(int[] arr, int d) {
        n = arr.length;
        this.d = d;
        this.arr = arr;
        f = new Integer[n];
        int ans = 1;
        for (int i = 0; i < n; ++i) {
            ans = Math.max(ans, dfs(i));
        }
        return ans;
    }

    private int dfs(int i) {
        if (f[i] != null) {
            return f[i];
        }
        int ans = 1;
        for (int j = i - 1; j >= 0; --j) {
            if (i - j > d || arr[j] >= arr[i]) {
                break;
            }
            ans = Math.max(ans, 1 + dfs(j));
        }
        for (int j = i + 1; j < n; ++j) {
            if (j - i > d || arr[j] >= arr[i]) {
                break;
            }
            ans = Math.max(ans, 1 + dfs(j));
        }
        return f[i] = ans;
    }
}

C++

class Solution {
public:
    int maxJumps(vector<int>& arr, int d) {
        int n = arr.size();
        int f[n];
        memset(f, 0, sizeof(f));
        function<int(int)> dfs = [&](int i) -> int {
            if (f[i]) {
                return f[i];
            }
            int ans = 1;
            for (int j = i - 1; j >= 0; --j) {
                if (i - j > d || arr[j] >= arr[i]) {
                    break;
                }
                ans = max(ans, 1 + dfs(j));
            }
            for (int j = i + 1; j < n; ++j) {
                if (j - i > d || arr[j] >= arr[i]) {
                    break;
                }
                ans = max(ans, 1 + dfs(j));
            }
            return f[i] = ans;
        };
        int ans = 1;
        for (int i = 0; i < n; ++i) {
            ans = max(ans, dfs(i));
        }
        return ans;
    }
};

Go

func maxJumps(arr []int, d int) (ans int) {
	n := len(arr)
	f := make([]int, n)
	var dfs func(int) int
	dfs = func(i int) int {
		if f[i] != 0 {
			return f[i]
		}
		ans := 1
		for j := i - 1; j >= 0; j-- {
			if i-j > d || arr[j] >= arr[i] {
				break
			}
			ans = max(ans, 1+dfs(j))
		}
		for j := i + 1; j < n; j++ {
			if j-i > d || arr[j] >= arr[i] {
				break
			}
			ans = max(ans, 1+dfs(j))
		}
		f[i] = ans
		return ans
	}
	for i := 0; i < n; i++ {
		ans = max(ans, dfs(i))
	}
	return
}

方法二：排序 + 动态规划

我们可以将数组 $arr$ 中的每个元素 $x$ 与其下标 $i$ 组成一个元组 $(x,i)$，并将这些元组按照 $x$ 从小到大排序。

接下来定义 $f[i]$ 表示从下标 $i$ 开始跳跃能够访问的最大下标数。初始时 $f[i]=1$，即每个下标都可以单独作为一次跳跃。

我们可以按照元组 $(x,i)$ 的顺序枚举 $i$，并枚举 $i$ 的所有合法的跳跃目标 $j$，即 $i-d\le j\le i+d$，并且 $arr[i]>arr[j]$。对于每个合法的 $j$，我们可以更新 $f[i]$ 的值，即 $f[i]=max(f[i],1+f[j])$。

最终的答案即为 $\underset{0\le i<n}{max}f[i]$。

时间复杂度 $O(n\log n+n\times d)$，空间复杂度 $O(n)$。其中 $n$ 为数组 $arr$ 的长度。

Python3

class Solution:
    def maxJumps(self, arr: List[int], d: int) -> int:
        n = len(arr)
        f = [1] * n
        for x, i in sorted(zip(arr, range(n))):
            for j in range(i - 1, -1, -1):
                if i - j > d or arr[j] >= x:
                    break
                f[i] = max(f[i], 1 + f[j])
            for j in range(i + 1, n):
                if j - i > d or arr[j] >= x:
                    break
                f[i] = max(f[i], 1 + f[j])
        return max(f)

Java

class Solution {
    public int maxJumps(int[] arr, int d) {
        int n = arr.length;
        Integer[] idx = new Integer[n];
        for (int i = 0; i < n; ++i) {
            idx[i] = i;
        }
        Arrays.sort(idx, (i, j) -> arr[i] - arr[j]);
        int[] f = new int[n];
        Arrays.fill(f, 1);
        int ans = 0;
        for (int i : idx) {
            for (int j = i - 1; j >= 0; --j) {
                if (i - j > d || arr[j] >= arr[i]) {
                    break;
                }
                f[i] = Math.max(f[i], 1 + f[j]);
            }
            for (int j = i + 1; j < n; ++j) {
                if (j - i > d || arr[j] >= arr[i]) {
                    break;
                }
                f[i] = Math.max(f[i], 1 + f[j]);
            }
            ans = Math.max(ans, f[i]);
        }
        return ans;
    }
}

C++

class Solution {
public:
    int maxJumps(vector<int>& arr, int d) {
        int n = arr.size();
        vector<int> idx(n);
        iota(idx.begin(), idx.end(), 0);
        sort(idx.begin(), idx.end(), [&](int i, int j) { return arr[i] < arr[j]; });
        vector<int> f(n, 1);
        for (int i : idx) {
            for (int j = i - 1; j >= 0; --j) {
                if (i - j > d || arr[j] >= arr[i]) {
                    break;
                }
                f[i] = max(f[i], 1 + f[j]);
            }
            for (int j = i + 1; j < n; ++j) {
                if (j - i > d || arr[j] >= arr[i]) {
                    break;
                }
                f[i] = max(f[i], 1 + f[j]);
            }
        }
        return *max_element(f.begin(), f.end());
    }
};

Go

func maxJumps(arr []int, d int) int {
	n := len(arr)
	idx := make([]int, n)
	f := make([]int, n)
	for i := range f {
		idx[i] = i
		f[i] = 1
	}
	sort.Slice(idx, func(i, j int) bool { return arr[idx[i]] < arr[idx[j]] })
	for _, i := range idx {
		for j := i - 1; j >= 0; j-- {
			if i-j > d || arr[j] >= arr[i] {
				break
			}
			f[i] = max(f[i], 1+f[j])
		}
		for j := i + 1; j < n; j++ {
			if j-i > d || arr[j] >= arr[i] {
				break
			}
			f[i] = max(f[i], 1+f[j])
		}
	}
	return slices.Max(f)
}