comments	difficulty	edit_url	tags
true	中等	https://github.com/doocs/leetcode/edit/main/solution/1600-1699/1650.Lowest%20Common%20Ancestor%20of%20a%20Binary%20Tree%20III/README.md	树 哈希表 双指针 二叉树

1650. 二叉树的最近公共祖先 III 🔒

English Version

题目描述

给定一棵二叉树中的两个节点 p 和 q，返回它们的最近公共祖先节点（LCA）。

每个节点都包含其父节点的引用（指针）。Node 的定义如下：

class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
}

根据维基百科中对最近公共祖先节点的定义：“两个节点 p 和 q 在二叉树 T 中的最近公共祖先节点是后代节点中既包括 p 又包括 q 的最深节点（我们允许一个节点为自身的一个后代节点）”。一个节点 x 的后代节点是节点 x 到某一叶节点间的路径中的节点 y。

 

示例 1:

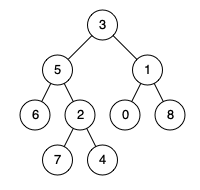
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和 1 的最近公共祖先是 3。

示例 2:

输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和 4 的最近公共祖先是 5，根据定义，一个节点可以是自身的最近公共祖先。

示例 3:

输入: root = [1,2], p = 1, q = 2
输出: 1

 

提示:

• 树中节点个数的范围是 [2, 105]。
• -109 <= Node.val <= 109
• 所有的 Node.val 都是互不相同的。
• p != q
• p 和 q 存在于树中。

解法

方法一：哈希表

我们用一个哈希表 $vis$ 记录从节点 $p$ 开始到根节点的路径上的所有节点，接下来从节点 $q$ 开始往根节点方向遍历，如果遇到一个节点存在于哈希表 $vis$ 中，那么该节点就是 $p$ 和 $q$ 的最近公共祖先节点，直接返回即可。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是二叉树的节点数。

Python3

"""
# Definition for a Node.
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None
        self.parent = None
"""


class Solution:
    def lowestCommonAncestor(self, p: "Node", q: "Node") -> "Node":
        vis = set()
        node = p
        while node:
            vis.add(node)
            node = node.parent
        node = q
        while node not in vis:
            node = node.parent
        return node

Java

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
};
*/

class Solution {
    public Node lowestCommonAncestor(Node p, Node q) {
        Set<Node> vis = new HashSet<>();
        for (Node node = p; node != null; node = node.parent) {
            vis.add(node);
        }
        for (Node node = q;; node = node.parent) {
            if (!vis.add(node)) {
                return node;
            }
        }
    }
}

C++

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* parent;
};
*/

class Solution {
public:
    Node* lowestCommonAncestor(Node* p, Node* q) {
        unordered_set<Node*> vis;
        for (Node* node = p; node; node = node->parent) {
            vis.insert(node);
        }
        for (Node* node = q;; node = node->parent) {
            if (vis.count(node)) {
                return node;
            }
        }
    }
};

Go

/**
 * Definition for Node.
 * type Node struct {
 *     Val int
 *     Left *Node
 *     Right *Node
 *     Parent *Node
 * }
 */

func lowestCommonAncestor(p *Node, q *Node) *Node {
	vis := map[*Node]bool{}
	for node := p; node != nil; node = node.Parent {
		vis[node] = true
	}
	for node := q; ; node = node.Parent {
		if vis[node] {
			return node
		}
	}
}

TypeScript

/**
 * Definition for a binary tree node.
 * class Node {
 *     val: number
 *     left: Node | null
 *     right: Node | null
 *     parent: Node | null
 *     constructor(val?: number, left?: Node | null, right?: Node | null, parent?: Node | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *         this.parent = (parent===undefined ? null : parent)
 *     }
 * }
 */

function lowestCommonAncestor(p: Node | null, q: Node | null): Node | null {
    const vis: Set<Node> = new Set();
    for (let node = p; node; node = node.parent) {
        vis.add(node);
    }
    for (let node = q; ; node = node.parent) {
        if (vis.has(node)) {
            return node;
        }
    }
}

方法二：双指针

我们可以用两个指针 $a$ 和 $b$ 分别指向节点 $p$ 和 $q$，然后分别往根节点方向遍历，当 $a$ 和 $b$ 相遇时，就是 $p$ 和 $q$ 的最近公共祖先节点。否则，如果指针 $a$ 遍历到了根节点，那么我们就让它指向节点 $q$，指针 $b$ 同理。这样，当两个指针相遇时，就是 $p$ 和 $q$ 的最近公共祖先节点。

时间复杂度 $O(n)$，其中 $n$ 是二叉树的节点数。空间复杂度 $O(1)$。

Python3

"""
# Definition for a Node.
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None
        self.parent = None
"""


class Solution:
    def lowestCommonAncestor(self, p: 'Node', q: 'Node') -> 'Node':
        a, b = p, q
        while a != b:
            a = a.parent if a.parent else q
            b = b.parent if b.parent else p
        return a

Java

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
};
*/

class Solution {
    public Node lowestCommonAncestor(Node p, Node q) {
        Node a = p, b = q;
        while (a != b) {
            a = a.parent == null ? q : a.parent;
            b = b.parent == null ? p : b.parent;
        }
        return a;
    }
}

C++

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;
    Node* parent;
};
*/

class Solution {
public:
    Node* lowestCommonAncestor(Node* p, Node* q) {
        Node* a = p;
        Node* b = q;
        while (a != b) {
            a = a->parent ? a->parent : q;
            b = b->parent ? b->parent : p;
        }
        return a;
    }
};

Go

/**
 * Definition for Node.
 * type Node struct {
 *     Val int
 *     Left *Node
 *     Right *Node
 *     Parent *Node
 * }
 */

func lowestCommonAncestor(p *Node, q *Node) *Node {
	a, b := p, q
	for a != b {
		if a.Parent != nil {
			a = a.Parent
		} else {
			a = q
		}
		if b.Parent != nil {
			b = b.Parent
		} else {
			b = p
		}
	}
	return a
}

TypeScript

/**
 * Definition for a binary tree node.
 * class Node {
 *     val: number
 *     left: Node | null
 *     right: Node | null
 *     parent: Node | null
 *     constructor(val?: number, left?: Node | null, right?: Node | null, parent?: Node | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *         this.parent = (parent===undefined ? null : parent)
 *     }
 * }
 */

function lowestCommonAncestor(p: Node | null, q: Node | null): Node | null {
    let [a, b] = [p, q];
    while (a != b) {
        a = a.parent ?? q;
        b = b.parent ?? p;
    }
    return a;
}