comments	difficulty	edit_url	tags
true	中等	https://github.com/doocs/leetcode/edit/main/solution/0200-0299/0223.Rectangle%20Area/README.md	几何 数学

223. 矩形面积

English Version

题目描述

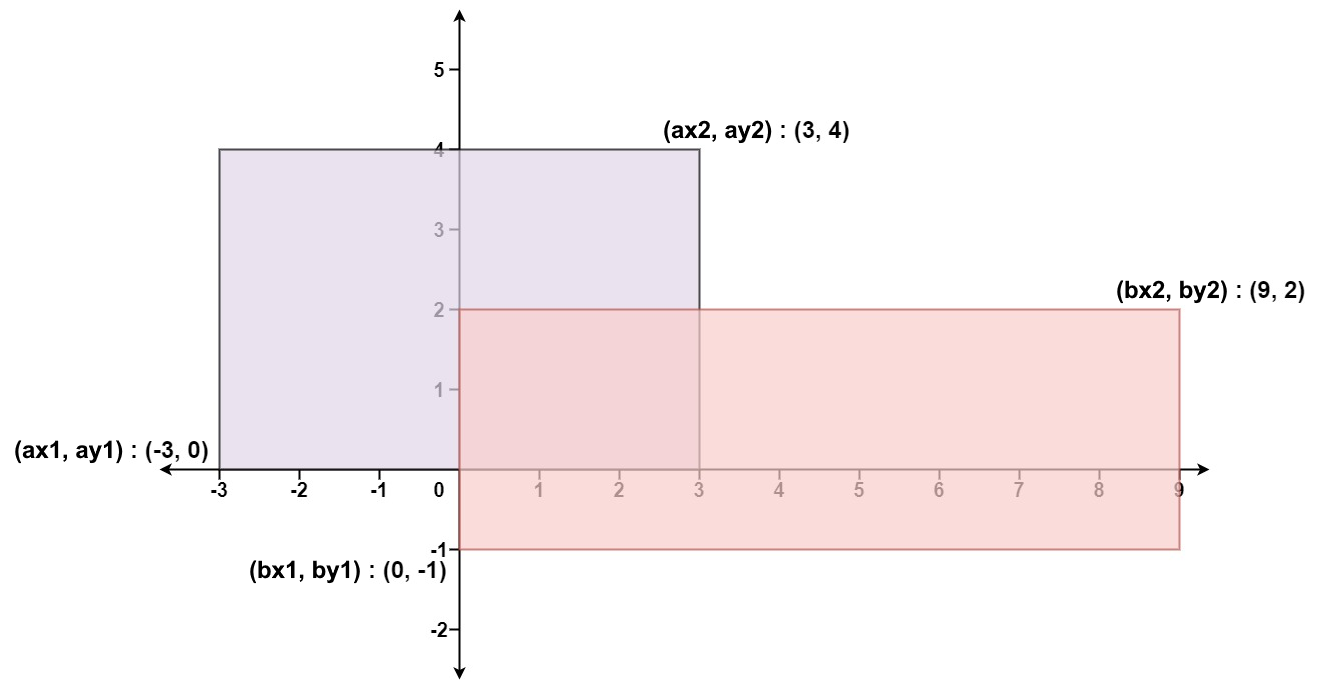
给你 二维 平面上两个 由直线构成且边与坐标轴平行/垂直 的矩形，请你计算并返回两个矩形覆盖的总面积。

每个矩形由其 左下 顶点和 右上 顶点坐标表示：

• 第一个矩形由其左下顶点 (ax1, ay1) 和右上顶点 (ax2, ay2) 定义。
• 第二个矩形由其左下顶点 (bx1, by1) 和右上顶点 (bx2, by2) 定义。

 

示例 1：

输入：ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
输出：45

示例 2：

输入：ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
输出：16

 

提示：

• -104 <= ax1, ay1, ax2, ay2, bx1, by1, bx2, by2 <= 104

解法

方法一：计算重叠面积

我们先计算出两个矩形各自的面积，记为 $a$ 和 $b$，然后计算重叠的宽度 $width$ 和高度 $height$，那么重叠的面积为 $max(width,0)\times max(height,0)$，最后将 $a$, $b$ 和重叠面积相减即可。

时间复杂度 $O(1)$，空间复杂度 $O(1)$。

Python3

class Solution:
    def computeArea(
        self,
        ax1: int,
        ay1: int,
        ax2: int,
        ay2: int,
        bx1: int,
        by1: int,
        bx2: int,
        by2: int,
    ) -> int:
        a = (ax2 - ax1) * (ay2 - ay1)
        b = (bx2 - bx1) * (by2 - by1)
        width = min(ax2, bx2) - max(ax1, bx1)
        height = min(ay2, by2) - max(ay1, by1)
        return a + b - max(height, 0) * max(width, 0)

Java

class Solution {
    public int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
        int a = (ax2 - ax1) * (ay2 - ay1);
        int b = (bx2 - bx1) * (by2 - by1);
        int width = Math.min(ax2, bx2) - Math.max(ax1, bx1);
        int height = Math.min(ay2, by2) - Math.max(ay1, by1);
        return a + b - Math.max(height, 0) * Math.max(width, 0);
    }
}

C++

class Solution {
public:
    int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
        int a = (ax2 - ax1) * (ay2 - ay1);
        int b = (bx2 - bx1) * (by2 - by1);
        int width = min(ax2, bx2) - max(ax1, bx1);
        int height = min(ay2, by2) - max(ay1, by1);
        return a + b - max(height, 0) * max(width, 0);
    }
};

Go

func computeArea(ax1 int, ay1 int, ax2 int, ay2 int, bx1 int, by1 int, bx2 int, by2 int) int {
	a := (ax2 - ax1) * (ay2 - ay1)
	b := (bx2 - bx1) * (by2 - by1)
	width := min(ax2, bx2) - max(ax1, bx1)
	height := min(ay2, by2) - max(ay1, by1)
	return a + b - max(height, 0)*max(width, 0)
}

TypeScript

function computeArea(
    ax1: number,
    ay1: number,
    ax2: number,
    ay2: number,
    bx1: number,
    by1: number,
    bx2: number,
    by2: number,
): number {
    const a = (ax2 - ax1) * (ay2 - ay1);
    const b = (bx2 - bx1) * (by2 - by1);
    const width = Math.min(ax2, bx2) - Math.max(ax1, bx1);
    const height = Math.min(ay2, by2) - Math.max(ay1, by1);
    return a + b - Math.max(width, 0) * Math.max(height, 0);
}

C#

public class Solution {
    public int ComputeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
        int a = (ax2 - ax1) * (ay2 - ay1);
        int b = (bx2 - bx1) * (by2 - by1);
        int width = Math.Min(ax2, bx2) - Math.Max(ax1, bx1);
        int height = Math.Min(ay2, by2) - Math.Max(ay1, by1);
        return a + b - Math.Max(height, 0) * Math.Max(width, 0);
    }
}