Skip to content

Latest commit

 

History

History
216 lines (175 loc) · 6.8 KB

README_EN.md

File metadata and controls

216 lines (175 loc) · 6.8 KB
comments difficulty edit_url tags
true
Medium
Array
Dynamic Programming
Matrix

3148. Maximum Difference Score in a Grid

中文文档

Description

You are given an m x n matrix grid consisting of positive integers. You can move from a cell in the matrix to any other cell that is either to the bottom or to the right (not necessarily adjacent). The score of a move from a cell with the value c1 to a cell with the value c2 is c2 - c1.

You can start at any cell, and you have to make at least one move.

Return the maximum total score you can achieve.

 

Example 1:

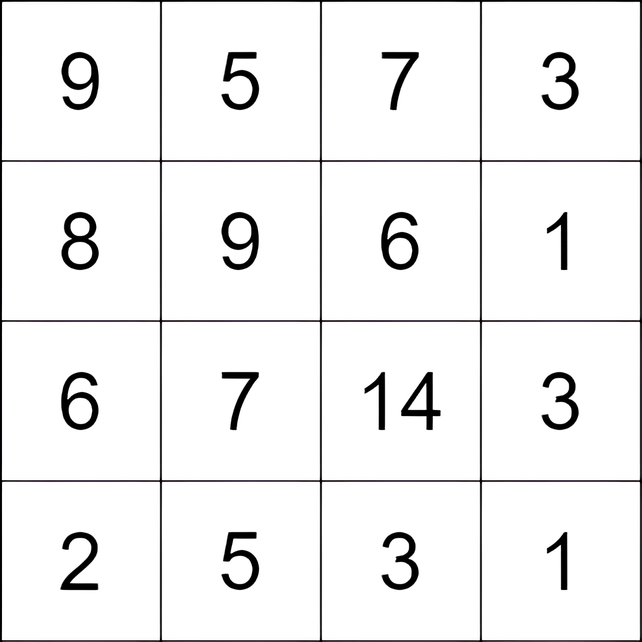
Input: grid = [[9,5,7,3],[8,9,6,1],[6,7,14,3],[2,5,3,1]]

Output: 9

Explanation: We start at the cell (0, 1), and we perform the following moves:
- Move from the cell (0, 1) to (2, 1) with a score of 7 - 5 = 2.
- Move from the cell (2, 1) to (2, 2) with a score of 14 - 7 = 7.
The total score is 2 + 7 = 9.

Example 2:

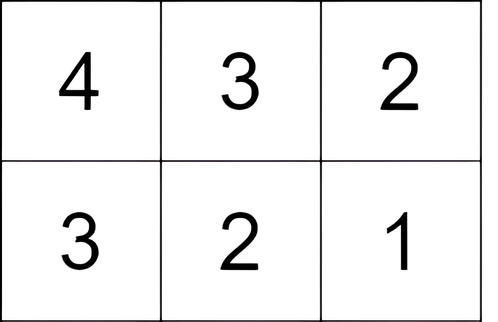
Input: grid = [[4,3,2],[3,2,1]]

Output: -1

Explanation: We start at the cell (0, 0), and we perform one move: (0, 0) to (0, 1). The score is 3 - 4 = -1.

 

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 2 <= m, n <= 1000
  • 4 <= m * n <= 105
  • 1 <= grid[i][j] <= 105

Solutions

Solution 1: Dynamic Programming

According to the problem description, if the values of the cells we pass through are $c_1, c_2, \cdots, c_k$, then our score is $c_2 - c_1 + c_3 - c_2 + \cdots + c_k - c_{k-1} = c_k - c_1$. Therefore, the problem is transformed into: for each cell $(i, j)$ of the matrix, if we take it as the endpoint, what is the minimum value of the starting point.

We can use dynamic programming to solve this problem. We define $f[i][j]$ as the minimum value of the path with $(i, j)$ as the endpoint. Then we can get the state transition equation:

$$ f[i][j] = \min(f[i-1][j], f[i][j-1], grid[i][j]) $$

So the answer is the maximum value of $\text{grid}[i][j] - \min(f[i-1][j], f[i][j-1])$.

The time complexity is $O(m \times n)$, and the space complexity is $O(m \times n)$. Where $m$ and $n$ are the number of rows and columns of the matrix, respectively.

Python3

class Solution:
    def maxScore(self, grid: List[List[int]]) -> int:
        f = [[0] * len(grid[0]) for _ in range(len(grid))]
        ans = -inf
        for i, row in enumerate(grid):
            for j, x in enumerate(row):
                mi = inf
                if i:
                    mi = min(mi, f[i - 1][j])
                if j:
                    mi = min(mi, f[i][j - 1])
                ans = max(ans, x - mi)
                f[i][j] = min(x, mi)
        return ans

Java

class Solution {
    public int maxScore(List<List<Integer>> grid) {
        int m = grid.size(), n = grid.get(0).size();
        final int inf = 1 << 30;
        int ans = -inf;
        int[][] f = new int[m][n];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                int mi = inf;
                if (i > 0) {
                    mi = Math.min(mi, f[i - 1][j]);
                }
                if (j > 0) {
                    mi = Math.min(mi, f[i][j - 1]);
                }
                ans = Math.max(ans, grid.get(i).get(j) - mi);
                f[i][j] = Math.min(grid.get(i).get(j), mi);
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int maxScore(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        const int inf = 1 << 30;
        int ans = -inf;
        int f[m][n];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                int mi = inf;
                if (i) {
                    mi = min(mi, f[i - 1][j]);
                }
                if (j) {
                    mi = min(mi, f[i][j - 1]);
                }
                ans = max(ans, grid[i][j] - mi);
                f[i][j] = min(grid[i][j], mi);
            }
        }
        return ans;
    }
};

Go

func maxScore(grid [][]int) int {
	m, n := len(grid), len(grid[0])
	f := make([][]int, m)
	for i := range f {
		f[i] = make([]int, n)
	}
	const inf int = 1 << 30
	ans := -inf
	for i, row := range grid {
		for j, x := range row {
			mi := inf
			if i > 0 {
				mi = min(mi, f[i-1][j])
			}
			if j > 0 {
				mi = min(mi, f[i][j-1])
			}
			ans = max(ans, x-mi)
			f[i][j] = min(x, mi)
		}
	}
	return ans
}

TypeScript

function maxScore(grid: number[][]): number {
    const [m, n] = [grid.length, grid[0].length];
    const f: number[][] = Array.from({ length: m }, () => Array.from({ length: n }, () => 0));
    let ans = -Infinity;
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            let mi = Infinity;
            if (i) {
                mi = Math.min(mi, f[i - 1][j]);
            }
            if (j) {
                mi = Math.min(mi, f[i][j - 1]);
            }
            ans = Math.max(ans, grid[i][j] - mi);
            f[i][j] = Math.min(mi, grid[i][j]);
        }
    }
    return ans;
}