README.md

1391. 检查网格中是否存在有效路径

English Version

题目描述

给你一个 m x n 的网格 grid。网格里的每个单元都代表一条街道。grid[i][j] 的街道可以是：

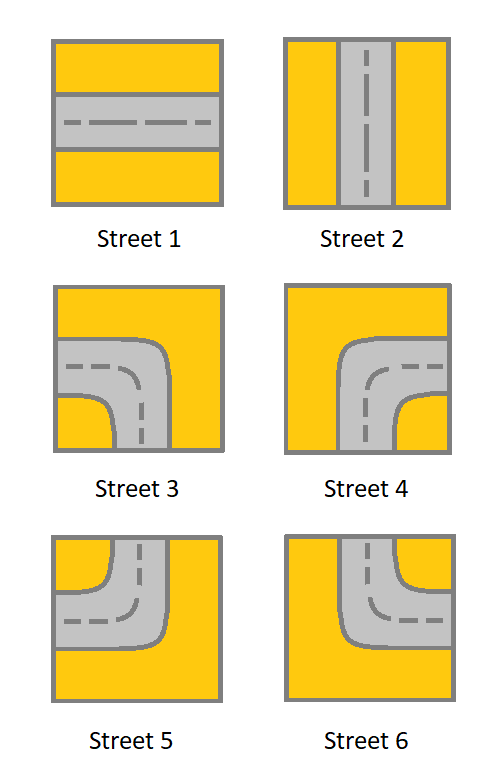
• 1 表示连接左单元格和右单元格的街道。
• 2 表示连接上单元格和下单元格的街道。
• 3 表示连接左单元格和下单元格的街道。
• 4 表示连接右单元格和下单元格的街道。
• 5 表示连接左单元格和上单元格的街道。
• 6 表示连接右单元格和上单元格的街道。

你最开始从左上角的单元格 (0,0) 开始出发，网格中的「有效路径」是指从左上方的单元格 (0,0) 开始、一直到右下方的 (m-1,n-1) 结束的路径。该路径必须只沿着街道走。

注意：你 不能 变更街道。

如果网格中存在有效的路径，则返回 true，否则返回 false 。

 

示例 1：

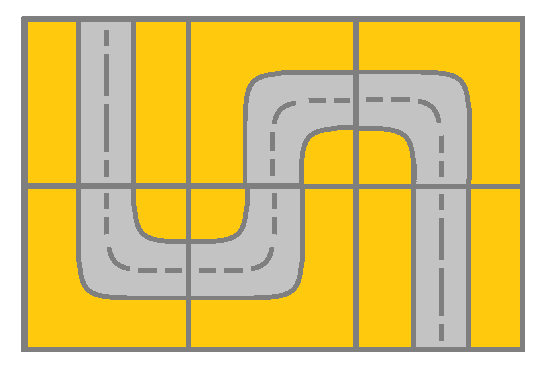
输入：grid = [[2,4,3],[6,5,2]]
输出：true
解释：如图所示，你可以从 (0, 0) 开始，访问网格中的所有单元格并到达 (m - 1, n - 1) 。

示例 2：

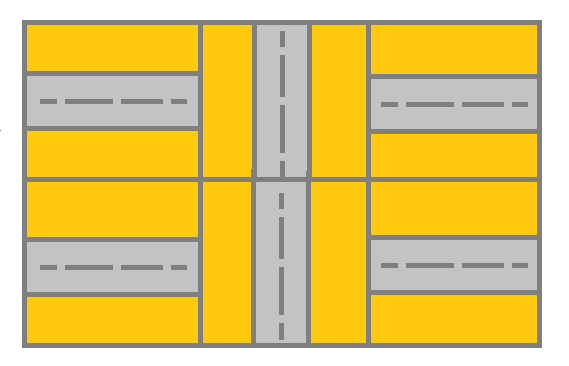
输入：grid = [[1,2,1],[1,2,1]]
输出：false
解释：如图所示，单元格 (0, 0) 上的街道没有与任何其他单元格上的街道相连，你只会停在 (0, 0) 处。

示例 3：

输入：grid = [[1,1,2]]
输出：false
解释：你会停在 (0, 1)，而且无法到达 (0, 2) 。

示例 4：

输入：grid = [[1,1,1,1,1,1,3]]
输出：true

示例 5：

输入：grid = [[2],[2],[2],[2],[2],[2],[6]]
输出：true

 

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 300
• 1 <= grid[i][j] <= 6

解法

并查集。

并查集模板：

模板 1——朴素并查集：

# 初始化，p存储每个点的父节点
p = list(range(n))

# 返回x的祖宗节点
def find(x):
    if p[x] != x:
        # 路径压缩
        p[x] = find(p[x])
    return p[x]

# 合并a和b所在的两个集合
p[find(a)] = find(b)

模板 2——维护 size 的并查集：

# 初始化，p存储每个点的父节点，size只有当节点是祖宗节点时才有意义，表示祖宗节点所在集合中，点的数量
p = list(range(n))
size = [1] * n

# 返回x的祖宗节点
def find(x):
    if p[x] != x:
        # 路径压缩
        p[x] = find(p[x])
    return p[x]

# 合并a和b所在的两个集合
if find(a) != find(b):
    size[find(b)] += size[find(a)]
    p[find(a)] = find(b)

模板 3——维护到祖宗节点距离的并查集：

# 初始化，p存储每个点的父节点，d[x]存储x到p[x]的距离
p = list(range(n))
d = [0] * n

# 返回x的祖宗节点
def find(x):
    if p[x] != x:
        t = find(p[x])
        d[x] += d[p[x]]
        p[x] = t
    return p[x]

# 合并a和b所在的两个集合
p[find(a)] = find(b)
d[find(a)] = distance

Python3

class Solution:
    def hasValidPath(self, grid: List[List[int]]) -> bool:
        m, n = len(grid), len(grid[0])
        p = list(range(m * n))

        def find(x):
            if p[x] != x:
                p[x] = find(p[x])
            return p[x]
        
        def left(i, j):
            if j > 0 and grid[i][j - 1] in (1, 4, 6):
                p[find(i * n + j)] = find(i * n + j - 1)
        
        def right(i, j):
            if j < n - 1 and grid[i][j + 1] in (1, 3, 5):
                p[find(i * n + j)] = find(i * n + j + 1)
        
        def up(i, j):
            if i > 0 and grid[i - 1][j] in (2, 3, 4):
                p[find(i * n + j)] = find((i - 1) * n + j)
        
        def down(i, j):
            if i < m - 1 and grid[i + 1][j] in (2, 5, 6):
                p[find(i * n + j)] = find((i + 1) * n + j)
        
        for i in range(m):
            for j in range(n):
                e = grid[i][j]
                if e == 1:
                    left(i, j)
                    right(i, j)
                elif e == 2:
                    up(i, j)
                    down(i, j)
                elif e == 3:
                    left(i, j)
                    down(i, j)
                elif e == 4:
                    right(i, j)
                    down(i, j)
                elif e == 5:
                    left(i, j)
                    up(i, j)
                else:
                    right(i, j)
                    up(i, j)
        return find(0) == find(m * n - 1)

Java

class Solution {
    private int[] p;
    private int[][] grid;
    private int m;
    private int n;

    public boolean hasValidPath(int[][] grid) {
        this.grid = grid;
        m = grid.length;
        n = grid[0].length;
        p = new int[m * n];
        for (int i = 0; i < p.length; ++i) {
            p[i] = i;
        }
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                int e = grid[i][j];
                if (e == 1) {
                    left(i, j);
                    right(i, j);
                } else if (e == 2) {
                    up(i, j);
                    down(i, j);
                } else if (e == 3) {
                    left(i, j);
                    down(i, j);
                } else if (e == 4) {
                    right(i, j);
                    down(i, j);
                } else if (e == 5) {
                    left(i, j);
                    up(i, j);
                } else {
                    right(i, j);
                    up(i, j);
                }
            }
        }
        return find(0) == find(m * n - 1);
    }

    private int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }

    private void left(int i, int j) {
        if (j > 0 && (grid[i][j - 1] == 1 || grid[i][j - 1] == 4 || grid[i][j - 1] == 6)) {
            p[find(i * n + j)] = find(i * n + j - 1);
        }
    }

    private void right(int i, int j) {
        if (j < n - 1 && (grid[i][j + 1] == 1 || grid[i][j + 1] == 3 || grid[i][j + 1] == 5)) {
            p[find(i * n + j)] = find(i * n + j + 1);
        }
    }

    private void up(int i, int j) {
        if (i > 0 && (grid[i - 1][j] == 2 || grid[i - 1][j] == 3 || grid[i - 1][j] == 4)) {
            p[find(i * n + j)] = find((i - 1) * n + j);
        }
    }

    private void down(int i, int j) {
        if (i < m - 1 && (grid[i + 1][j] == 2 || grid[i + 1][j] == 5 || grid[i + 1][j] == 6)) {
            p[find(i * n + j)] = find((i + 1) * n + j);
        }
    }
}

...