comments	difficulty	edit_url	rating	source	tags
true	简单	https://github.com/doocs/leetcode/edit/main/solution/1800-1899/1886.Determine%20Whether%20Matrix%20Can%20Be%20Obtained%20By%20Rotation/README.md	1407	第 244 场周赛 Q1	数组 矩阵

1886. 判断矩阵经轮转后是否一致

English Version

题目描述

给你两个大小为 n x n 的二进制矩阵 mat 和 target 。现 以 90 度顺时针轮转 矩阵 mat 中的元素 若干次 ，如果能够使 mat 与 target 一致，返回 true ；否则，返回 false 。

 

示例 1：

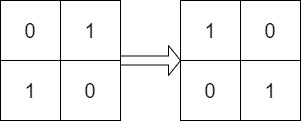
输入：mat = [[0,1],[1,0]], target = [[1,0],[0,1]]
输出：true
解释：顺时针轮转 90 度一次可以使 mat 和 target 一致。

示例 2：

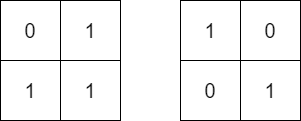
输入：mat = [[0,1],[1,1]], target = [[1,0],[0,1]]
输出：false
解释：无法通过轮转矩阵中的元素使 equal 与 target 一致。

示例 3：

输入：mat = [[0,0,0],[0,1,0],[1,1,1]], target = [[1,1,1],[0,1,0],[0,0,0]]
输出：true
解释：顺时针轮转 90 度两次可以使 mat 和 target 一致。

 

提示：

• n == mat.length == target.length
• n == mat[i].length == target[i].length
• 1 <= n <= 10
• mat[i][j] 和 target[i][j] 不是 0 就是 1

解法

方法一：模拟旋转

旋转矩阵，判断矩阵是否一致，旋转方式同 48. 旋转图像。

Python3

class Solution:
    def findRotation(self, mat: List[List[int]], target: List[List[int]]) -> bool:
        def rotate(matrix):
            n = len(matrix)
            for i in range(n // 2):
                for j in range(i, n - 1 - i):
                    t = matrix[i][j]
                    matrix[i][j] = matrix[n - j - 1][i]
                    matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1]
                    matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1]
                    matrix[j][n - i - 1] = t

        for _ in range(4):
            if mat == target:
                return True
            rotate(mat)
        return False

Java

class Solution {
    public boolean findRotation(int[][] mat, int[][] target) {
        int times = 4;
        while (times-- > 0) {
            if (equals(mat, target)) {
                return true;
            }
            rotate(mat);
        }
        return false;
    }

    private void rotate(int[][] matrix) {
        int n = matrix.length;
        for (int i = 0; i < n / 2; ++i) {
            for (int j = i; j < n - 1 - i; ++j) {
                int t = matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][i];
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = t;
            }
        }
    }

    private boolean equals(int[][] nums1, int[][] nums2) {
        int n = nums1.length;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (nums1[i][j] != nums2[i][j]) {
                    return false;
                }
            }
        }
        return true;
    }
}

C++

class Solution {
public:
    bool findRotation(vector<vector<int>>& mat, vector<vector<int>>& target) {
        int n = mat.size();
        for (int k = 0; k < 4; ++k) {
            vector<vector<int>> g(n, vector<int>(n));
            for (int i = 0; i < n; ++i)
                for (int j = 0; j < n; ++j)
                    g[i][j] = mat[j][n - i - 1];
            if (g == target) return true;
            mat = g;
        }
        return false;
    }
};

Go

func findRotation(mat [][]int, target [][]int) bool {
	n := len(mat)
	for k := 0; k < 4; k++ {
		g := make([][]int, n)
		for i := range g {
			g[i] = make([]int, n)
		}
		for i := 0; i < n; i++ {
			for j := 0; j < n; j++ {
				g[i][j] = mat[j][n-i-1]
			}
		}
		if equals(g, target) {
			return true
		}
		mat = g
	}
	return false
}

func equals(a, b [][]int) bool {
	for i, row := range a {
		for j, v := range row {
			if v != b[i][j] {
				return false
			}
		}
	}
	return true
}

TypeScript

function findRotation(mat: number[][], target: number[][]): boolean {
    for (let k = 0; k < 4; k++) {
        rotate(mat);
        if (isEqual(mat, target)) {
            return true;
        }
    }
    return false;
}

function isEqual(A: number[][], B: number[][]) {
    const n = A.length;
    for (let i = 0; i < n; i++) {
        for (let j = 0; j < n; j++) {
            if (A[i][j] !== B[i][j]) {
                return false;
            }
        }
    }
    return true;
}

function rotate(matrix: number[][]): void {
    const n = matrix.length;
    for (let i = 0; i < n >> 1; i++) {
        for (let j = 0; j < (n + 1) >> 1; j++) {
            [
                matrix[i][j],
                matrix[n - 1 - j][i],
                matrix[n - 1 - i][n - 1 - j],
                matrix[j][n - 1 - i],
            ] = [
                matrix[n - 1 - j][i],
                matrix[n - 1 - i][n - 1 - j],
                matrix[j][n - 1 - i],
                matrix[i][j],
            ];
        }
    }
}

Rust

impl Solution {
    pub fn find_rotation(mat: Vec<Vec<i32>>, target: Vec<Vec<i32>>) -> bool {
        let n = mat.len();
        let mut is_equal = [true; 4];
        for i in 0..n {
            for j in 0..n {
                if is_equal[0] && mat[i][j] != target[i][j] {
                    is_equal[0] = false;
                }
                if is_equal[1] && mat[i][j] != target[j][n - 1 - i] {
                    is_equal[1] = false;
                }
                if is_equal[2] && mat[i][j] != target[n - 1 - i][n - 1 - j] {
                    is_equal[2] = false;
                }
                if is_equal[3] && mat[i][j] != target[n - 1 - j][i] {
                    is_equal[3] = false;
                }
            }
        }
        is_equal.into_iter().any(|&v| v)
    }
}

方法二：原地比较

此题不同于 48. 旋转图像，并不要求改动原数组，因此，只要比较对应的位置即可。

旋转度数	A	B
0	i, j	i, j
90	i, j	j, n - i
180	i, j	n - i, n - j
270	i, j	n - j, i

n = A.length - 1 = B.length - 1

Python3

class Solution:
    def findRotation(self, mat: List[List[int]], target: List[List[int]]) -> bool:
        for _ in range(4):
            mat = [list(col) for col in zip(*mat[::-1])]
            if mat == target:
                return True
        return False

Java

class Solution {
    public boolean findRotation(int[][] mat, int[][] target) {
        int n = mat.length;
        for (int k = 0; k < 4; ++k) {
            int[][] g = new int[n][n];
            for (int i = 0; i < n; ++i) {
                for (int j = 0; j < n; ++j) {
                    g[i][j] = mat[j][n - i - 1];
                }
            }
            if (equals(g, target)) {
                return true;
            }
            mat = g;
        }
        return false;
    }

    private boolean equals(int[][] a, int[][] b) {
        int n = a.length;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < n; ++j) {
                if (a[i][j] != b[i][j]) {
                    return false;
                }
            }
        }
        return true;
    }
}