| comments | difficulty | edit_url | rating | source | tags | ||||
|---|---|---|---|---|---|---|---|---|---|
true |
困难 |
2275 |
第 36 场双周赛 Q4 |
|
你有 k 个服务器,编号为 0 到 k-1 ,它们可以同时处理多个请求组。每个服务器有无穷的计算能力但是 不能同时处理超过一个请求 。请求分配到服务器的规则如下:
- 第
i(序号从 0 开始)个请求到达。 - 如果所有服务器都已被占据,那么该请求被舍弃(完全不处理)。
- 如果第
(i % k)个服务器空闲,那么对应服务器会处理该请求。 - 否则,将请求安排给下一个空闲的服务器(服务器构成一个环,必要的话可能从第 0 个服务器开始继续找下一个空闲的服务器)。比方说,如果第
i个服务器在忙,那么会查看第(i+1)个服务器,第(i+2)个服务器等等。
给你一个 严格递增 的正整数数组 arrival ,表示第 i 个任务的到达时间,和另一个数组 load ,其中 load[i] 表示第 i 个请求的工作量(也就是服务器完成它所需要的时间)。你的任务是找到 最繁忙的服务器 。最繁忙定义为一个服务器处理的请求数是所有服务器里最多的。
请你返回包含所有 最繁忙服务器 序号的列表,你可以以任意顺序返回这个列表。
示例 1:
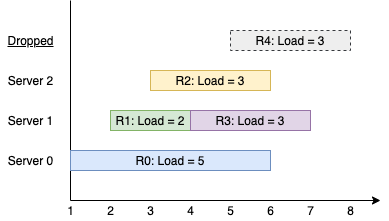
输入:k = 3, arrival = [1,2,3,4,5], load = [5,2,3,3,3] 输出:[1] 解释: 所有服务器一开始都是空闲的。 前 3 个请求分别由前 3 台服务器依次处理。 请求 3 进来的时候,服务器 0 被占据,所以它被安排到下一台空闲的服务器,也就是服务器 1 。 请求 4 进来的时候,由于所有服务器都被占据,该请求被舍弃。 服务器 0 和 2 分别都处理了一个请求,服务器 1 处理了两个请求。所以服务器 1 是最忙的服务器。
示例 2:
输入:k = 3, arrival = [1,2,3,4], load = [1,2,1,2] 输出:[0] 解释: 前 3 个请求分别被前 3 个服务器处理。 请求 3 进来,由于服务器 0 空闲,它被服务器 0 处理。 服务器 0 处理了两个请求,服务器 1 和 2 分别处理了一个请求。所以服务器 0 是最忙的服务器。
示例 3:
输入:k = 3, arrival = [1,2,3], load = [10,12,11] 输出:[0,1,2] 解释:每个服务器分别处理了一个请求,所以它们都是最忙的服务器。
示例 4:
输入:k = 3, arrival = [1,2,3,4,8,9,10], load = [5,2,10,3,1,2,2] 输出:[1]
示例 5:
输入:k = 1, arrival = [1], load = [1] 输出:[0]
提示:
1 <= k <= 1051 <= arrival.length, load.length <= 105arrival.length == load.length1 <= arrival[i], load[i] <= 109arrival保证 严格递增 。
题目求的是最繁忙的服务器列表,因此可以想到用哈希表记录每个服务器处理的任务数,然后获取所有处理了最大任务数 mx 的服务器列表即可。关键的问题就在于,求出每个任务分配给了哪台服务器处理。
我们用 有序集合 free 存放所有的空闲服务器,优先队列 busy 存放正在处理请求的服务器的处理结束时间和对应的服务器编号,即二元组 (end, server),优先队列满足队首元素的处理结束时间最小,用一个哈希表 cnt 记录每台服务器处理的任务数。
当第 i 个请求到达时,如果 busy 不为空,我们循环判断 busy 队首的任务结束时间是否小于等于当前请求的到达时间 arrival[i],即 start。如果是,说明队首任务在此时刻已经处理结束,可以从 busy 队列中移出,循环判断。
接下来,如果 free 为空,说明当前没有空闲服务器能够处理第 i 个请求,直接 continue 丢弃;否则,查找 free 中大于等于 i % k 的第一个服务器,如果查找成功,那么由该服务器来处理该请求,否则,由 free 的第一个服务器(编号最小)来处理。假设该服务器是 server, 那么 cnt[server] 加 1,同时将二元组 (end, server) 放入优先队列 busy 中,并且将该 server 中有序集合 free 中移出。
最后,只需要获取 cnt 中的最大值 mx,找出处理了 mx 个任务数的服务器列表,即为答案。
class Solution:
def busiestServers(self, k: int, arrival: List[int], load: List[int]) -> List[int]:
free = SortedList(range(k))
busy = []
cnt = [0] * k
for i, (start, t) in enumerate(zip(arrival, load)):
while busy and busy[0][0] <= start:
free.add(busy[0][1])
heappop(busy)
if not free:
continue
j = free.bisect_left(i % k)
if j == len(free):
j = 0
server = free[j]
cnt[server] += 1
heappush(busy, (start + t, server))
free.remove(server)
mx = max(cnt)
return [i for i, v in enumerate(cnt) if v == mx]class Solution {
public List<Integer> busiestServers(int k, int[] arrival, int[] load) {
int[] cnt = new int[k];
PriorityQueue<int[]> busy = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
TreeSet<Integer> free = new TreeSet<>();
for (int i = 0; i < k; ++i) {
free.add(i);
}
for (int i = 0; i < arrival.length; ++i) {
int start = arrival[i];
int end = start + load[i];
while (!busy.isEmpty() && busy.peek()[0] <= start) {
free.add(busy.poll()[1]);
}
if (free.isEmpty()) {
continue;
}
Integer server = free.ceiling(i % k);
if (server == null) {
server = free.first();
}
++cnt[server];
busy.offer(new int[] {end, server});
free.remove(server);
}
int mx = 0;
for (int v : cnt) {
mx = Math.max(mx, v);
}
List<Integer> ans = new ArrayList<>();
for (int i = 0; i < k; ++i) {
if (cnt[i] == mx) {
ans.add(i);
}
}
return ans;
}
}class Solution {
public:
vector<int> busiestServers(int k, vector<int>& arrival, vector<int>& load) {
set<int> free;
for (int i = 0; i < k; ++i) free.insert(i);
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> busy;
vector<int> cnt(k);
for (int i = 0; i < arrival.size(); ++i) {
int start = arrival[i], end = start + load[i];
while (!busy.empty() && busy.top().first <= start) {
free.insert(busy.top().second);
busy.pop();
}
if (free.empty()) continue;
auto p = free.lower_bound(i % k);
if (p == free.end()) p = free.begin();
int server = *p;
++cnt[server];
busy.emplace(end, server);
free.erase(server);
}
int mx = *max_element(cnt.begin(), cnt.end());
vector<int> ans;
for (int i = 0; i < k; ++i)
if (cnt[i] == mx)
ans.push_back(i);
return ans;
}
};func busiestServers(k int, arrival, load []int) (ans []int) {
free := redblacktree.NewWithIntComparator()
for i := 0; i < k; i++ {
free.Put(i, nil)
}
busy := hp{}
cnt := make([]int, k)
for i, t := range arrival {
for len(busy) > 0 && busy[0].end <= t {
free.Put(busy[0].server, nil)
heap.Pop(&busy)
}
if free.Size() == 0 {
continue
}
p, _ := free.Ceiling(i % k)
if p == nil {
p = free.Left()
}
server := p.Key.(int)
cnt[server]++
heap.Push(&busy, pair{t + load[i], server})
free.Remove(server)
}
mx := slices.Max(cnt)
for i, v := range cnt {
if v == mx {
ans = append(ans, i)
}
}
return
}
type pair struct{ end, server int }
type hp []pair
func (h hp) Len() int { return len(h) }
func (h hp) Less(i, j int) bool { return h[i].end < h[j].end }
func (h hp) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
func (h *hp) Push(v any) { *h = append(*h, v.(pair)) }
func (h *hp) Pop() any { a := *h; v := a[len(a)-1]; *h = a[:len(a)-1]; return v }