2152. 穿过所有点的所需最少直线数量

English Version

题目描述

给定一个 points 数组，points[i] = [xi, yi] 表示直角坐标系 X-Y 的一个点。

现在考虑向 X-Y 坐标系中添加 直线，使得每个点 至少 在一条直线上。

返回能够穿过所有点的所需 最少直线 数量。

 

示例 1:

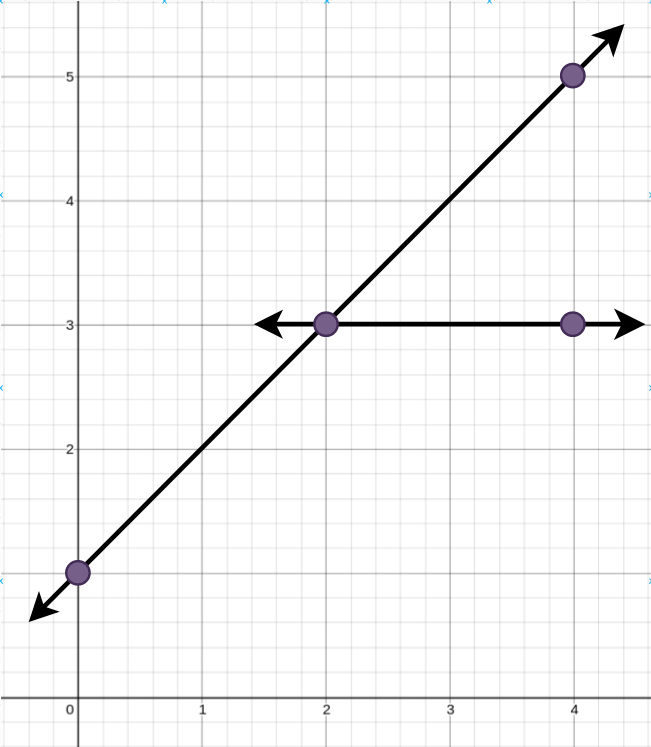
输入: points = [[0,1],[2,3],[4,5],[4,3]]
输出: 2
解释: 所需最少直线数量为 2 ，一种可能的答案是添加:
- 一条穿过点 (0, 1) 和 点(4, 5) 的直线
- 另一条穿过点 (2, 3) 和点 (4, 3) 的直线

示例 2:

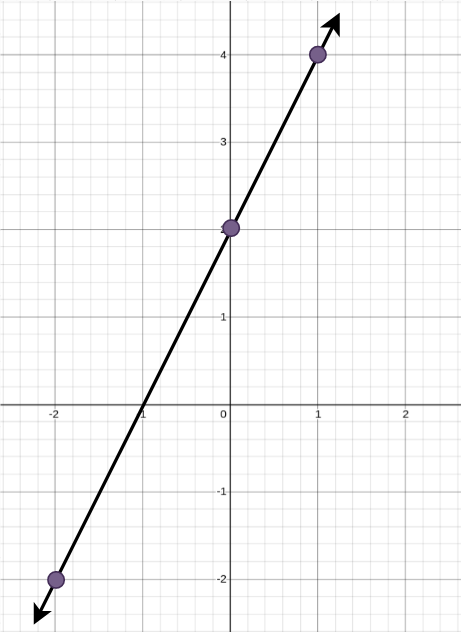
输入: points = [[0,2],[-2,-2],[1,4]]
输出: 1
解释: 所需最少直线数量为 1 ，唯一的答案是:
- 一条穿过点 (-2, -2) 和点 (1, 4) 的直线

 

提示:

• 1 <= points.length <= 10
• points[i].length == 2
• -100 <= xi, yi <= 100
• points 中元素都是唯一的

解法

方法一：状态压缩 + 记忆化搜索

我们可以用一个整数 state 来表示当前已经添加的直线，其中 state 的第 $i$ 位表示第 $i$ 条直线是否已经添加。如果 state 的第 $i$ 位为 $1$，则表示第 $i$ 条直线已经添加，否则表示第 $i$ 条直线还未添加。

接下来，我们设计一个函数 $dfs(state)$，表示当前已经添加的直线为 state 时，至少需要添加多少条直线才能使得每个点至少在一条直线上。那么答案就是 $dfs(0)$。

函数 $dfs(state)$ 的计算过程如下：

• 如果 state 的所有位都为 $1$，则说明所有直线都已经添加，返回 $0$。
• 否则，我们枚举当前还未添加的点 $i$，接下来枚举 $j$，我们将 $i$ 和 $j$ 的点连成一条直线，此时的状态为 $nxt = state | 1 &lt;&lt; i | 1 &lt;&lt; j$，其中 $1 &lt;&lt; i$ 表示将第 $i$ 位设置为 $1$，$1 << j$ 表示将第 $j$ 位设置为 $1$。接下来，我们枚举所有 $k$，如果 $i$、$j$ 和 $k$ 三个点共线，则将 $k$ 的状态设置为 $1$，即 $nxt = nxt | 1 &lt;&lt; k$。此时，我们可以将 $i$ 和 $j$ 以及 $k$ 这三个点连成一条直线，此时的状态为 $nxt$，此时至少需要添加 $dfs(nxt)$ 条直线，我们取所有情况的最小值，即为 $dfs(state)$ 的值。

为了避免重复计算，我们可以使用记忆化搜索。

时间复杂度 $O(2^n \times n^3)$，空间复杂度 $O(2^n)$。其中 $n$ 为点的数量。

Python3

class Solution:
    def minimumLines(self, points: List[List[int]]) -> int:
        def check(i, j, k):
            x1, y1 = points[i]
            x2, y2 = points[j]
            x3, y3 = points[k]
            return (x2 - x1) * (y3 - y1) == (x3 - x1) * (y2 - y1)

        @cache
        def dfs(state):
            if state == (1 << n) - 1:
                return 0
            ans = inf
            for i in range(n):
                if not (state >> i & 1):
                    for j in range(i + 1, n):
                        nxt = state | 1 << i | 1 << j
                        for k in range(j + 1, n):
                            if not (nxt >> k & 1) and check(i, j, k):
                                nxt |= 1 << k
                        ans = min(ans, dfs(nxt) + 1)
                    if i == n - 1:
                        ans = min(ans, dfs(state | 1 << i) + 1)
            return ans

        n = len(points)
        return dfs(0)

Java

class Solution {
    private int[] f;
    private int[][] points;
    private int n;

    public int minimumLines(int[][] points) {
        n = points.length;
        this.points = points;
        f = new int[1 << n];
        return dfs(0);
    }

    private int dfs(int state) {
        if (state == (1 << n) - 1) {
            return 0;
        }
        if (f[state] != 0) {
            return f[state];
        }
        int ans = 1 << 30;
        for (int i = 0; i < n; ++i) {
            if (((state >> i) & 1) == 0) {
                for (int j = i + 1; j < n; ++j) {
                    int nxt = state | 1 << i | 1 << j;
                    for (int k = j + 1; k < n; ++k) {
                        if (((state >> k) & 1) == 0 && check(i, j, k)) {
                            nxt |= 1 << k;
                        }
                    }
                    ans = Math.min(ans, dfs(nxt) + 1);
                }
                if (i == n - 1) {
                    ans = Math.min(ans, dfs(state | 1 << i) + 1);
                }
            }
        }
        return f[state] = ans;
    }

    private boolean check(int i, int j, int k) {
        int x1 = points[i][0], y1 = points[i][1];
        int x2 = points[j][0], y2 = points[j][1];
        int x3 = points[k][0], y3 = points[k][1];
        return (x2 - x1) * (y3 - y1) == (x3 - x1) * (y2 - y1);
    }
}

C++

class Solution {
public:
    int minimumLines(vector<vector<int>>& points) {
        auto check = [&](int i, int j, int k) {
            int x1 = points[i][0], y1 = points[i][1];
            int x2 = points[j][0], y2 = points[j][1];
            int x3 = points[k][0], y3 = points[k][1];
            return (x2 - x1) * (y3 - y1) == (x3 - x1) * (y2 - y1);
        };
        int n = points.size();
        int f[1 << n];
        memset(f, 0, sizeof f);
        function<int(int)> dfs = [&](int state) -> int {
            if (state == (1 << n) - 1) return 0;
            if (f[state]) return f[state];
            int ans = 1 << 30;
            for (int i = 0; i < n; ++i) {
                if (!(state >> i & 1)) {
                    for (int j = i + 1; j < n; ++j) {
                        int nxt = state | 1 << i | 1 << j;
                        for (int k = j + 1; k < n; ++k) {
                            if (!(nxt >> k & 1) && check(i, j, k)) {
                                nxt |= 1 << k;
                            }
                        }
                        ans = min(ans, dfs(nxt) + 1);
                    }
                    if (i == n - 1) {
                        ans = min(ans, dfs(state | 1 << i) + 1);
                    }
                }
            }
            return f[state] = ans;
        };
        return dfs(0);
    }
};

Go

func minimumLines(points [][]int) int {
	check := func(i, j, k int) bool {
		x1, y1 := points[i][0], points[i][1]
		x2, y2 := points[j][0], points[j][1]
		x3, y3 := points[k][0], points[k][1]
		return (x2-x1)*(y3-y1) == (x3-x1)*(y2-y1)
	}
	n := len(points)
	f := make([]int, 1<<n)
	var dfs func(int) int
	dfs = func(state int) int {
		if state == (1<<n)-1 {
			return 0
		}
		if f[state] > 0 {
			return f[state]
		}
		ans := 1 << 30
		for i := 0; i < n; i++ {
			if (state >> i & 1) == 0 {
				for j := i + 1; j < n; j++ {
					nxt := state | 1<<i | 1<<j
					for k := j + 1; k < n; k++ {
						if (nxt>>k&1) == 0 && check(i, j, k) {
							nxt |= 1 << k
						}
					}
					ans = min(ans, dfs(nxt)+1)
				}
				if i == n-1 {
					ans = min(ans, dfs(state|1<<i)+1)
				}
			}
		}
		f[state] = ans
		return ans
	}
	return dfs(0)
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

TypeScript

...