LCP 34. 二叉树染色

题目描述

小扣有一个根结点为 root 的二叉树模型，初始所有结点均为白色，可以用蓝色染料给模型结点染色，模型的每个结点有一个 val 价值。小扣出于美观考虑，希望最后二叉树上每个蓝色相连部分的结点个数不能超过 k 个，求所有染成蓝色的结点价值总和最大是多少？

示例 1：

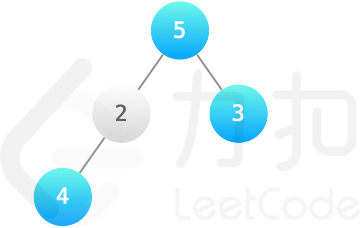
输入：root = [5,2,3,4], k = 2

输出：12

解释：结点 5、3、4 染成蓝色，获得最大的价值 5+3+4=12 >

示例 2：

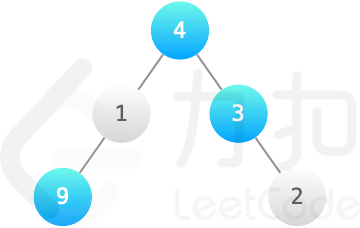
输入：root = [4,1,3,9,null,null,2], k = 2

输出：16

解释：结点 4、3、9 染成蓝色，获得最大的价值 4+3+9=16

提示：

• 1 <= k <= 10
• 1 <= val <= 10000
• 1 <= 结点数量 <= 10000

解法

方法一：动态规划（树形 DP）

我们考虑以 $root$ 为根节点的子树，且 $root$ 节点连着 $t$ 个染色节点的最大价值，其中 $t\in [0,k]$。我们用状态 $f[root][t]$ 来表示。

如果我们不染色 $root$ 节点，那么 $root$ 的左右节点可以连着 $t\in [0,k]$ 个染色节点，即 $f[root][0]=\underset{t\in [0,k]}{max}f[root.left][t]+\underset{t\in [0,k]}{max}f[root.right][t]$。

如果我们染色 $root$ 节点，那么 $root$ 的左右节点可以连着最多共 $k-1$ 个染色节点，不妨假设左节点连着 $i$ 个染色节点，右节点连着 $j$ 个染色节点，其中 $i\in [0,k-1]$, $j\in [0,k-1-i]$，那么 $f[root][i+j+1]=\underset{i\in [0,k-1],j\in [0,k-1-i]}{max}f[root.left][i]+f[root.right][j]+root.val$。

最后答案就是 $f[root][t]$ 中的最大值。

时间复杂度 $O(n\times k^2)$，空间复杂度 $O(n\times k)$。其中 $n$ 和 $k$ 分别是二叉树的节点数和 $k$ 的值。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None


class Solution:
    def maxValue(self, root: TreeNode, k: int) -> int:
        def dfs(root: TreeNode) -> List[int]:
            ans = [0] * (k + 1)
            if root is None:
                return ans
            l, r = dfs(root.left), dfs(root.right)
            ans[0] = max(l) + max(r)
            for i in range(k):
                for j in range(k - i):
                    ans[i + j + 1] = max(ans[i + j + 1], l[i] + r[j] + root.val)
            return ans

        return max(dfs(root))

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    private int k;

    public int maxValue(TreeNode root, int k) {
        this.k = k;
        return Arrays.stream(dfs(root)).max().getAsInt();
    }

    private int[] dfs(TreeNode root) {
        int[] ans = new int[k + 1];
        if (root == null) {
            return ans;
        }
        int[] l = dfs(root.left);
        int[] r = dfs(root.right);
        ans[0] = Arrays.stream(l).max().getAsInt() + Arrays.stream(r).max().getAsInt();
        for (int i = 0; i < k; ++i) {
            for (int j = 0; j < k - i; ++j) {
                ans[i + j + 1] = Math.max(ans[i + j + 1], root.val + l[i] + r[j]);
            }
        }
        return ans;
    }
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxValue(TreeNode* root, int k) {
        function<vector<int>(TreeNode*)> dfs = [&](TreeNode* root) -> vector<int> {
            vector<int> ans(k + 1);
            if (!root) {
                return ans;
            }
            vector<int> l = dfs(root->left);
            vector<int> r = dfs(root->right);
            ans[0] = *max_element(l.begin(), l.end()) + *max_element(r.begin(), r.end());
            for (int i = 0; i < k; ++i) {
                for (int j = 0; j < k - i; ++j) {
                    ans[i + j + 1] = max(ans[i + j + 1], l[i] + r[j] + root->val);
                }
            }
            return ans;
        };
        vector<int> ans = dfs(root);
        return *max_element(ans.begin(), ans.end());
    }
};

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func maxValue(root *TreeNode, k int) int {
	var dfs func(*TreeNode) []int
	dfs = func(node *TreeNode) []int {
		ans := make([]int, k+1)
		if node == nil {
			return ans
		}
		l := dfs(node.Left)
		r := dfs(node.Right)
		ans[0] = slices.Max(l) + slices.Max(r)
		for i := 0; i < k; i++ {
			for j := 0; j < k-i; j++ {
				ans[i+j+1] = max(ans[i+j+1], l[i]+r[j]+node.Val)
			}
		}
		return ans
	}
	return slices.Max(dfs(root))
}

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} k
 * @return {number}
 */
var maxValue = function (root, k) {
    const dfs = root => {
        const ans = Array(k + 1).fill(0);
        if (!root) {
            return ans;
        }
        const l = dfs(root.left);
        const r = dfs(root.right);
        ans[0] = Math.max(...l) + Math.max(...r);
        for (let i = 0; i < k; i++) {
            for (let j = 0; j < k - i; ++j) {
                ans[i + j + 1] = Math.max(ans[i + j + 1], l[i] + r[j] + root.val);
            }
        }
        return ans;
    };
    return Math.max(...dfs(root));
};