LCP 67. 装饰树

题目描述

力扣嘉年华上的 DIY 手工展位准备了一棵缩小版的 二叉 装饰树 root 和灯饰，你需要将灯饰逐一插入装饰树中，要求如下：

• 完成装饰的二叉树根结点与 root 的根结点值相同
• 若一个节点拥有父节点，则在该节点和他的父节点之间插入一个灯饰（即插入一个值为 -1 的节点）。具体地：
  • 在一个 父节点 x 与其左子节点 y 之间添加 -1 节点， 节点 -1、节点 y 为各自父节点的左子节点，
  • 在一个 父节点 x 与其右子节点 y 之间添加 -1 节点， 节点 -1、节点 y 为各自父节点的右子节点，

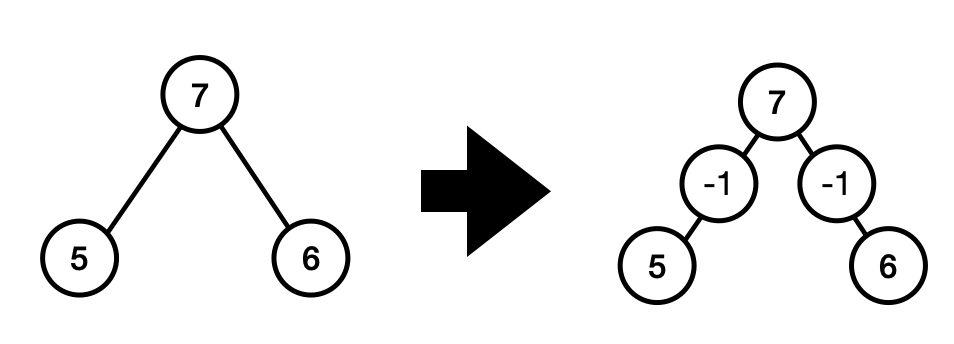
现给定二叉树的根节点 root ，请返回完成装饰后的树的根节点。 示例 1：

输入： root = [7,5,6]

输出：[7,-1,-1,5,null,null,6]

解释：如下图所示，

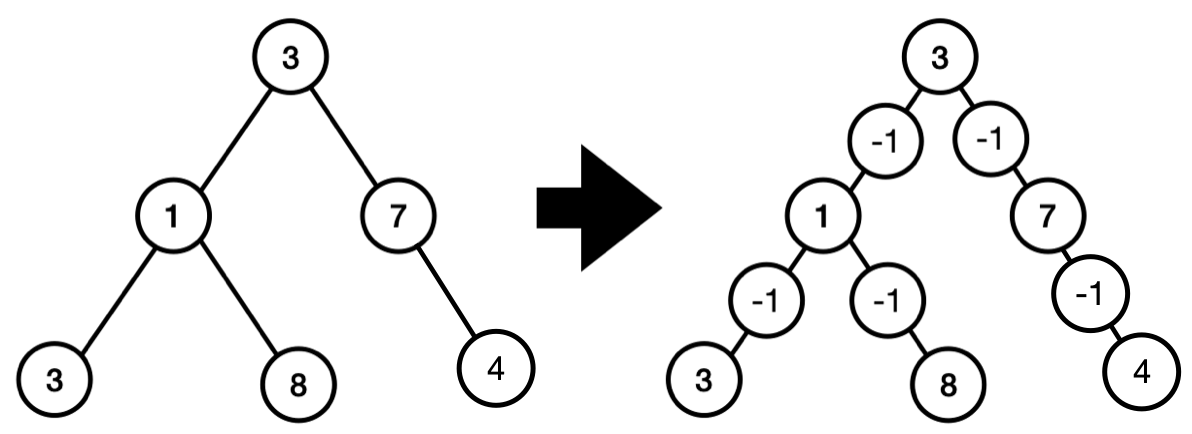
示例 2：

输入： root = [3,1,7,3,8,null,4]

输出：[3,-1,-1,1,null,null,7,-1,-1,null,-1,3,null,null,8,null,4]

解释：如下图所示

提示：

0 <= root.Val <= 1000 >root 节点数量范围为 [1, 10^5]

解法

方法一：递归

我们设计一个函数 $dfs(root)$，表示将灯饰插入以 $root$ 为根节点的树中，返回插入灯饰后的树的根节点。那么答案就是 $dfs(root)$。

函数 $dfs(root)$ 的逻辑如下：

• 若 $root$ 为空，则返回空；
• 否则，递归地对 $root$ 的左右子树分别调用 $dfs$ 函数，得到插入灯饰后的左右子树的根节点 $l$ 和 $r$；
• 若 $l$ 不为空，则我们创建一个新节点 $TreeNode(-1,l,null)$，并将其作为 $root$ 的左子节点；
• 若 $r$ 不为空，则我们创建一个新节点 $TreeNode(-1,null,r)$，并将其作为 $root$ 的右子节点；

最后，返回 $root$。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是树的节点数。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def expandBinaryTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        def dfs(root):
            if root is None:
                return None
            l, r = dfs(root.left), dfs(root.right)
            if l:
                root.left = TreeNode(-1, l)
            if r:
                root.right = TreeNode(-1, None, r)
            return root

        return dfs(root)

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode expandBinaryTree(TreeNode root) {
        return dfs(root);
    }

    private TreeNode dfs(TreeNode root) {
        if (root == null) {
            return null;
        }
        TreeNode l = dfs(root.left);
        TreeNode r = dfs(root.right);
        if (l != null) {
            root.left = new TreeNode(-1, l, null);
        }
        if (r != null) {
            root.right = new TreeNode(-1, null, r);
        }
        return root;
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* expandBinaryTree(TreeNode* root) {
        function<TreeNode*(TreeNode*)> dfs = [&](TreeNode* root) -> TreeNode* {
            if (!root) {
                return nullptr;
            }
            TreeNode* l = dfs(root->left);
            TreeNode* r = dfs(root->right);
            if (l) {
                root->left = new TreeNode(-1, l, nullptr);
            }
            if (r) {
                root->right = new TreeNode(-1, nullptr, r);
            }
            return root;
        };
        return dfs(root);
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func expandBinaryTree(root *TreeNode) *TreeNode {
	var dfs func(*TreeNode) *TreeNode
	dfs = func(root *TreeNode) *TreeNode {
		if root == nil {
			return root
		}
		l, r := dfs(root.Left), dfs(root.Right)
		if l != nil {
			root.Left = &TreeNode{-1, l, nil}
		}
		if r != nil {
			root.Right = &TreeNode{-1, nil, r}
		}
		return root
	}
	return dfs(root)
}

...