| comments | difficulty | edit_url | rating | source | tags | |||
|---|---|---|---|---|---|---|---|---|
true |
中等 |
1438 |
第 209 场周赛 Q2 |
|
如果一棵二叉树满足下述几个条件,则可以称为 奇偶树 :
- 二叉树根节点所在层下标为
0,根的子节点所在层下标为1,根的孙节点所在层下标为2,依此类推。 - 偶数下标 层上的所有节点的值都是 奇 整数,从左到右按顺序 严格递增
- 奇数下标 层上的所有节点的值都是 偶 整数,从左到右按顺序 严格递减
给你二叉树的根节点,如果二叉树为 奇偶树 ,则返回 true ,否则返回 false 。
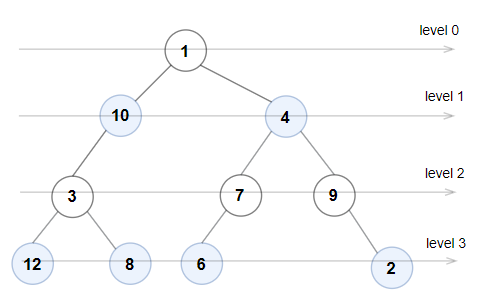
示例 1:
输入:root = [1,10,4,3,null,7,9,12,8,6,null,null,2] 输出:true 解释:每一层的节点值分别是: 0 层:[1] 1 层:[10,4] 2 层:[3,7,9] 3 层:[12,8,6,2] 由于 0 层和 2 层上的节点值都是奇数且严格递增,而 1 层和 3 层上的节点值都是偶数且严格递减,因此这是一棵奇偶树。
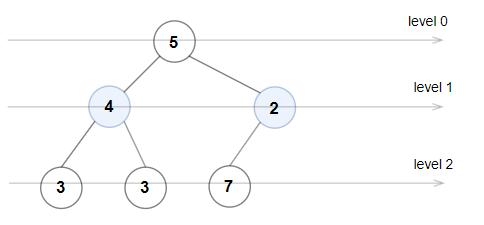
示例 2:
输入:root = [5,4,2,3,3,7] 输出:false 解释:每一层的节点值分别是: 0 层:[5] 1 层:[4,2] 2 层:[3,3,7] 2 层上的节点值不满足严格递增的条件,所以这不是一棵奇偶树。
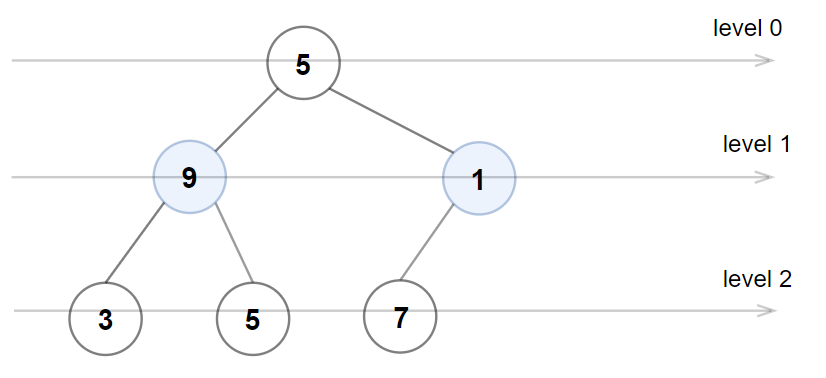
示例 3:
输入:root = [5,9,1,3,5,7] 输出:false 解释:1 层上的节点值应为偶数。
示例 4:
输入:root = [1] 输出:true
示例 5:
输入:root = [11,8,6,1,3,9,11,30,20,18,16,12,10,4,2,17] 输出:true
提示:
- 树中节点数在范围
[1, 105]内 1 <= Node.val <= 106
BFS 逐层遍历,每层按照奇偶性判断,每层的节点值都是偶数或奇数,且严格递增或递减。
时间复杂度
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isEvenOddTree(self, root: Optional[TreeNode]) -> bool:
even = 1
q = deque([root])
while q:
prev = 0 if even else inf
for _ in range(len(q)):
root = q.popleft()
if even and (root.val % 2 == 0 or prev >= root.val):
return False
if not even and (root.val % 2 == 1 or prev <= root.val):
return False
prev = root.val
if root.left:
q.append(root.left)
if root.right:
q.append(root.right)
even ^= 1
return True/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isEvenOddTree(TreeNode root) {
boolean even = true;
Deque<TreeNode> q = new ArrayDeque<>();
q.offer(root);
while (!q.isEmpty()) {
int prev = even ? 0 : 1000001;
for (int n = q.size(); n > 0; --n) {
root = q.pollFirst();
if (even && (root.val % 2 == 0 || prev >= root.val)) {
return false;
}
if (!even && (root.val % 2 == 1 || prev <= root.val)) {
return false;
}
prev = root.val;
if (root.left != null) {
q.offer(root.left);
}
if (root.right != null) {
q.offer(root.right);
}
}
even = !even;
}
return true;
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isEvenOddTree(TreeNode* root) {
int even = 1;
queue<TreeNode*> q{{root}};
while (!q.empty()) {
int prev = even ? 0 : 1e7;
for (int n = q.size(); n; --n) {
root = q.front();
q.pop();
if (even && (root->val % 2 == 0 || prev >= root->val)) {
return false;
}
if (!even && (root->val % 2 == 1 || prev <= root->val)) {
return false;
}
prev = root->val;
if (root->left) {
q.push(root->left);
}
if (root->right) {
q.push(root->right);
}
}
even ^= 1;
}
return true;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func isEvenOddTree(root *TreeNode) bool {
even := true
q := []*TreeNode{root}
for len(q) > 0 {
var prev int = 1e7
if even {
prev = 0
}
for n := len(q); n > 0; n-- {
root = q[0]
q = q[1:]
if even && (root.Val%2 == 0 || prev >= root.Val) {
return false
}
if !even && (root.Val%2 == 1 || prev <= root.Val) {
return false
}
prev = root.Val
if root.Left != nil {
q = append(q, root.Left)
}
if root.Right != nil {
q = append(q, root.Right)
}
}
even = !even
}
return true
}DFS 先序遍历二叉树,同样根据节点所在层的奇偶性判断是否满足条件,遍历过程中用哈希表记录每一层最近访问到的节点值。
时间复杂度
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isEvenOddTree(self, root: Optional[TreeNode]) -> bool:
def dfs(root, i):
if root is None:
return True
even = i % 2 == 0
prev = d.get(i, 0 if even else inf)
if even and (root.val % 2 == 0 or prev >= root.val):
return False
if not even and (root.val % 2 == 1 or prev <= root.val):
return False
d[i] = root.val
return dfs(root.left, i + 1) and dfs(root.right, i + 1)
d = {}
return dfs(root, 0)/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private Map<Integer, Integer> d = new HashMap<>();
public boolean isEvenOddTree(TreeNode root) {
return dfs(root, 0);
}
private boolean dfs(TreeNode root, int i) {
if (root == null) {
return true;
}
boolean even = i % 2 == 0;
int prev = d.getOrDefault(i, even ? 0 : 1000001);
if (even && (root.val % 2 == 0 || prev >= root.val)) {
return false;
}
if (!even && (root.val % 2 == 1 || prev <= root.val)) {
return false;
}
d.put(i, root.val);
return dfs(root.left, i + 1) && dfs(root.right, i + 1);
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
unordered_map<int, int> d;
bool isEvenOddTree(TreeNode* root) {
return dfs(root, 0);
}
bool dfs(TreeNode* root, int i) {
if (!root) {
return true;
}
int even = i % 2 == 0;
int prev = d.count(i) ? d[i] : (even ? 0 : 1e7);
if (even && (root->val % 2 == 0 || prev >= root->val)) {
return false;
}
if (!even && (root->val % 2 == 1 || prev <= root->val)) {
return false;
}
d[i] = root->val;
return dfs(root->left, i + 1) && dfs(root->right, i + 1);
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func isEvenOddTree(root *TreeNode) bool {
d := map[int]int{}
var dfs func(*TreeNode, int) bool
dfs = func(root *TreeNode, i int) bool {
if root == nil {
return true
}
even := i%2 == 0
prev, ok := d[i]
if !ok {
if even {
prev = 0
} else {
prev = 10000000
}
}
if even && (root.Val%2 == 0 || prev >= root.Val) {
return false
}
if !even && (root.Val%2 == 1 || prev <= root.Val) {
return false
}
d[i] = root.Val
return dfs(root.Left, i+1) && dfs(root.Right, i+1)
}
return dfs(root, 0)
}