514. 自由之路

English Version

题目描述

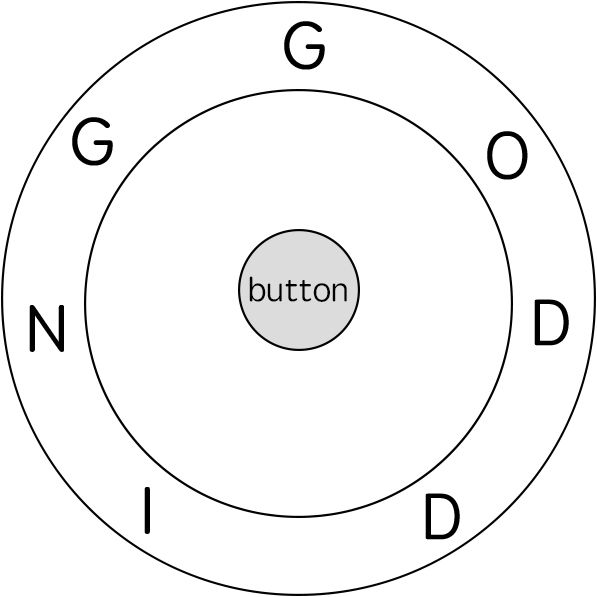
电子游戏“辐射4”中，任务 “通向自由” 要求玩家到达名为 “Freedom Trail Ring” 的金属表盘，并使用表盘拼写特定关键词才能开门。

给定一个字符串 ring ，表示刻在外环上的编码；给定另一个字符串 key ，表示需要拼写的关键词。您需要算出能够拼写关键词中所有字符的最少步数。

最初，ring 的第一个字符与 12:00 方向对齐。您需要顺时针或逆时针旋转 ring 以使 key 的一个字符在 12:00 方向对齐，然后按下中心按钮，以此逐个拼写完 key 中的所有字符。

旋转 ring 拼出 key 字符 key[i] 的阶段中：

1. 您可以将 ring 顺时针或逆时针旋转 一个位置 ，计为1步。旋转的最终目的是将字符串 ring 的一个字符与 12:00 方向对齐，并且这个字符必须等于字符 key[i] 。
2. 如果字符 key[i] 已经对齐到12:00方向，您需要按下中心按钮进行拼写，这也将算作 1 步。按完之后，您可以开始拼写 key 的下一个字符（下一阶段）, 直至完成所有拼写。

 

示例 1：

 

输入: ring = "godding", key = "gd"
输出: 4
解释:
 对于 key 的第一个字符 'g'，已经在正确的位置, 我们只需要1步来拼写这个字符。 
 对于 key 的第二个字符 'd'，我们需要逆时针旋转 ring "godding" 2步使它变成 "ddinggo"。
 当然, 我们还需要1步进行拼写。
 因此最终的输出是 4。

示例 2:

输入: ring = "godding", key = "godding"
输出: 13

 

提示：

• 1 <= ring.length, key.length <= 100
• ring 和 key 只包含小写英文字母
• 保证 字符串 key 一定可以由字符串  ring 旋转拼出

解法

方法一：动态规划

我们首先预处理出字符串 $ring$ 中每个字符 $c$ 出现的位置列表，记录在数组 $pos[c]$ 中。不妨假设字符串 $key$ 和 $ring$ 的长度分别为 $m$ 和 $n$。

然后我们定义 $f[i][j]$ 表示拼写完字符串 $key$ 的前 $i+1$ 个字符，且 $ring$ 的第 $j$ 个字符与 $12:00$ 方向对齐的最少步数。初始时 $f[i][j]=+\infty$。答案为 $\min_{0 \leq j < n} f[m - 1][j]$。

我们可以先初始化 $f[0][j]$，其中 $j$ 是字符 $key[0]$ 在 $ring$ 中出现的位置。由于 $ring$ 的第 $j$ 个字符与 $12:00$ 方向对齐，因此我们只需要 $1$ 步即可拼写出 $key[0]$。此外，我们还需要 $min(j, n - j)$ 步将 $ring$ 旋转到 $12:00$ 方向。因此 $f[0][j]=min(j, n - j) + 1$。

接下来，我们考虑当 $i \geq 1$ 时，状态如何转移。我们可以枚举 $key[i]$ 在 $ring$ 中的位置列表 $pos[key[i]]$，并枚举 $key[i-1]$ 在 $ring$ 中的位置列表 $pos[key[i-1]]$，然后更新 $f[i][j]$，即 $f[i][j]=\min_{k \in pos[key[i-1]]} f[i-1][k] + \min(\text{abs}(j - k), n - \text{abs}(j - k)) + 1$。

最后，我们返回 $\min_{0 \leq j \lt n} f[m - 1][j]$ 即可。

时间复杂度 $O(m \times n^2)$，空间复杂度 $O(m \times n)$。其中 $m$ 和 $n$ 分别是字符串 $key$ 和 $ring$ 的长度。

Python3

class Solution:
    def findRotateSteps(self, ring: str, key: str) -> int:
        m, n = len(key), len(ring)
        pos = defaultdict(list)
        for i, c in enumerate(ring):
            pos[c].append(i)
        f = [[inf] * n for _ in range(m)]
        for j in pos[key[0]]:
            f[0][j] = min(j, n - j) + 1
        for i in range(1, m):
            for j in pos[key[i]]:
                for k in pos[key[i - 1]]:
                    f[i][j] = min(
                        f[i][j], f[i - 1][k] + min(abs(j - k), n - abs(j - k)) + 1
                    )
        return min(f[-1][j] for j in pos[key[-1]])

Java

class Solution {
    public int findRotateSteps(String ring, String key) {
        int m = key.length(), n = ring.length();
        List<Integer>[] pos = new List[26];
        Arrays.setAll(pos, k -> new ArrayList<>());
        for (int i = 0; i < n; ++i) {
            int j = ring.charAt(i) - 'a';
            pos[j].add(i);
        }
        int[][] f = new int[m][n];
        for (var g : f) {
            Arrays.fill(g, 1 << 30);
        }
        for (int j : pos[key.charAt(0) - 'a']) {
            f[0][j] = Math.min(j, n - j) + 1;
        }
        for (int i = 1; i < m; ++i) {
            for (int j : pos[key.charAt(i) - 'a']) {
                for (int k : pos[key.charAt(i - 1) - 'a']) {
                    f[i][j] = Math.min(
                        f[i][j], f[i - 1][k] + Math.min(Math.abs(j - k), n - Math.abs(j - k)) + 1);
                }
            }
        }
        int ans = 1 << 30;
        for (int j : pos[key.charAt(m - 1) - 'a']) {
            ans = Math.min(ans, f[m - 1][j]);
        }
        return ans;
    }
}

C++

class Solution {
public:
    int findRotateSteps(string ring, string key) {
        int m = key.size(), n = ring.size();
        vector<int> pos[26];
        for (int j = 0; j < n; ++j) {
            pos[ring[j] - 'a'].push_back(j);
        }
        int f[m][n];
        memset(f, 0x3f, sizeof(f));
        for (int j : pos[key[0] - 'a']) {
            f[0][j] = min(j, n - j) + 1;
        }
        for (int i = 1; i < m; ++i) {
            for (int j : pos[key[i] - 'a']) {
                for (int k : pos[key[i - 1] - 'a']) {
                    f[i][j] = min(f[i][j], f[i - 1][k] + min(abs(j - k), n - abs(j - k)) + 1);
                }
            }
        }
        int ans = 1 << 30;
        for (int j : pos[key[m - 1] - 'a']) {
            ans = min(ans, f[m - 1][j]);
        }
        return ans;
    }
};

Go

func findRotateSteps(ring string, key string) int {
	m, n := len(key), len(ring)
	pos := [26][]int{}
	for j, c := range ring {
		pos[c-'a'] = append(pos[c-'a'], j)
	}
	f := make([][]int, m)
	for i := range f {
		f[i] = make([]int, n)
		for j := range f[i] {
			f[i][j] = 1 << 30
		}
	}
	for _, j := range pos[key[0]-'a'] {
		f[0][j] = min(j, n-j) + 1
	}
	for i := 1; i < m; i++ {
		for _, j := range pos[key[i]-'a'] {
			for _, k := range pos[key[i-1]-'a'] {
				f[i][j] = min(f[i][j], f[i-1][k]+min(abs(j-k), n-abs(j-k))+1)
			}
		}
	}
	ans := 1 << 30
	for _, j := range pos[key[m-1]-'a'] {
		ans = min(ans, f[m-1][j])
	}
	return ans
}

func abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}

...