给你一个数组 nums 表示 1 到 n 的一个排列。我们按照元素在 nums 中的顺序依次插入一个初始为空的二叉搜索树(BST)。请你统计将 nums 重新排序后,统计满足如下条件的方案数:重排后得到的二叉搜索树与 nums 原本数字顺序得到的二叉搜索树相同。
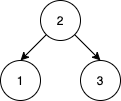
比方说,给你 nums = [2,1,3],我们得到一棵 2 为根,1 为左孩子,3 为右孩子的树。数组 [2,3,1] 也能得到相同的 BST,但 [3,2,1] 会得到一棵不同的 BST 。
请你返回重排 nums 后,与原数组 nums 得到相同二叉搜索树的方案数。
由于答案可能会很大,请将结果对 10^9 + 7 取余数。
示例 1:
输入:nums = [2,1,3] 输出:1 解释:我们将 nums 重排, [2,3,1] 能得到相同的 BST 。没有其他得到相同 BST 的方案了。
示例 2:
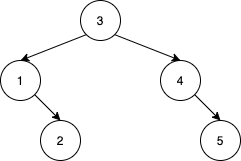
输入:nums = [3,4,5,1,2] 输出:5 解释:下面 5 个数组会得到相同的 BST: [3,1,2,4,5] [3,1,4,2,5] [3,1,4,5,2] [3,4,1,2,5] [3,4,1,5,2]
示例 3:
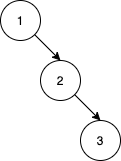
输入:nums = [1,2,3] 输出:0 解释:没有别的排列顺序能得到相同的 BST 。
提示:
1 <= nums.length <= 10001 <= nums[i] <= nums.lengthnums中所有数 互不相同 。
我们设计一个函数
接下来,我们来看一下
对于一个数组
其中
注意答案的取模运算,因为
时间复杂度
class Solution:
def numOfWays(self, nums: List[int]) -> int:
def dfs(nums):
if len(nums) < 2:
return 1
left = [x for x in nums if x < nums[0]]
right = [x for x in nums if x > nums[0]]
m, n = len(left), len(right)
a, b = dfs(left), dfs(right)
return (((c[m + n][m] * a) % mod) * b) % mod
n = len(nums)
mod = 10**9 + 7
c = [[0] * n for _ in range(n)]
c[0][0] = 1
for i in range(1, n):
c[i][0] = 1
for j in range(1, i + 1):
c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod
return (dfs(nums) - 1 + mod) % modclass Solution {
private int[][] c;
private final int mod = (int) 1e9 + 7;
public int numOfWays(int[] nums) {
int n = nums.length;
c = new int[n][n];
c[0][0] = 1;
for (int i = 1; i < n; ++i) {
c[i][0] = 1;
for (int j = 1; j <= i; ++j) {
c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
}
}
List<Integer> list = new ArrayList<>();
for (int x : nums) {
list.add(x);
}
return (dfs(list) - 1 + mod) % mod;
}
private int dfs(List<Integer> nums) {
if (nums.size() < 2) {
return 1;
}
List<Integer> left = new ArrayList<>();
List<Integer> right = new ArrayList<>();
for (int x : nums) {
if (x < nums.get(0)) {
left.add(x);
} else if (x > nums.get(0)) {
right.add(x);
}
}
int m = left.size(), n = right.size();
int a = dfs(left), b = dfs(right);
return (int) ((long) a * b % mod * c[m + n][n] % mod);
}
}class Solution {
public:
int numOfWays(vector<int>& nums) {
int n = nums.size();
const int mod = 1e9 + 7;
int c[n][n];
memset(c, 0, sizeof(c));
c[0][0] = 1;
for (int i = 1; i < n; ++i) {
c[i][0] = 1;
for (int j = 1; j <= i; ++j) {
c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
}
}
function<int(vector<int>)> dfs = [&](vector<int> nums) -> int {
if (nums.size() < 2) {
return 1;
}
vector<int> left, right;
for (int& x : nums) {
if (x < nums[0]) {
left.push_back(x);
} else if (x > nums[0]) {
right.push_back(x);
}
}
int m = left.size(), n = right.size();
int a = dfs(left), b = dfs(right);
return c[m + n][m] * 1ll * a % mod * b % mod;
};
return (dfs(nums) - 1 + mod) % mod;
}
};func numOfWays(nums []int) int {
n := len(nums)
const mod = 1e9 + 7
c := make([][]int, n)
for i := range c {
c[i] = make([]int, n)
}
c[0][0] = 1
for i := 1; i < n; i++ {
c[i][0] = 1
for j := 1; j <= i; j++ {
c[i][j] = (c[i-1][j] + c[i-1][j-1]) % mod
}
}
var dfs func(nums []int) int
dfs = func(nums []int) int {
if len(nums) < 2 {
return 1
}
var left, right []int
for _, x := range nums[1:] {
if x < nums[0] {
left = append(left, x)
} else {
right = append(right, x)
}
}
m, n := len(left), len(right)
a, b := dfs(left), dfs(right)
return c[m+n][m] * a % mod * b % mod
}
return (dfs(nums) - 1 + mod) % mod
}function numOfWays(nums: number[]): number {
const n = nums.length;
const mod = 1e9 + 7;
const c = new Array(n).fill(0).map(() => new Array(n).fill(0));
c[0][0] = 1;
for (let i = 1; i < n; ++i) {
c[i][0] = 1;
for (let j = 1; j <= i; ++j) {
c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % mod;
}
}
const dfs = (nums: number[]): number => {
if (nums.length < 2) {
return 1;
}
const left: number[] = [];
const right: number[] = [];
for (let i = 1; i < nums.length; ++i) {
if (nums[i] < nums[0]) {
left.push(nums[i]);
} else {
right.push(nums[i]);
}
}
const m = left.length;
const n = right.length;
const a = dfs(left);
const b = dfs(right);
return Number((BigInt(c[m + n][m]) * BigInt(a) * BigInt(b)) % BigInt(mod));
};
return (dfs(nums) - 1 + mod) % mod;
}