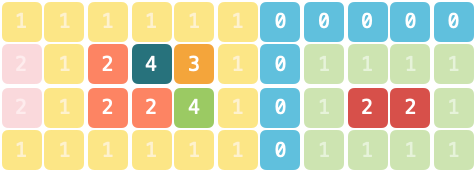
「以扣会友」线下活动所在场地由若干主题空间与走廊组成,场地的地图记作由一维字符串型数组 grid,字符串中仅包含 "0"~"5" 这 6 个字符。地图上每一个字符代表面积为 1 的区域,其中 "0" 表示走廊,其他字符表示主题空间。相同且连续(连续指上、下、左、右四个方向连接)的字符组成同一个主题空间。
假如整个 grid 区域的外侧均为走廊。请问,不与走廊直接相邻的主题空间的最大面积是多少?如果不存在这样的空间请返回 0。
示例 1:
输入:
grid = ["110","231","221"]输出:
1
示例 2:
输入:
grid = ["11111100000","21243101111","21224101221","11111101111"]输出:
3
提示:
1 <= grid.length <= 5001 <= grid[i].length <= 500grid[i][j]仅可能是"0"~"5"
并查集。
并查集模板:
模板 1——朴素并查集:
# 初始化,p存储每个点的父节点
p = list(range(n))
# 返回x的祖宗节点
def find(x):
if p[x] != x:
# 路径压缩
p[x] = find(p[x])
return p[x]
# 合并a和b所在的两个集合
p[find(a)] = find(b)模板 2——维护 size 的并查集:
# 初始化,p存储每个点的父节点,size只有当节点是祖宗节点时才有意义,表示祖宗节点所在集合中,点的数量
p = list(range(n))
size = [1] * n
# 返回x的祖宗节点
def find(x):
if p[x] != x:
# 路径压缩
p[x] = find(p[x])
return p[x]
# 合并a和b所在的两个集合
if find(a) != find(b):
size[find(b)] += size[find(a)]
p[find(a)] = find(b)模板 3——维护到祖宗节点距离的并查集:
# 初始化,p存储每个点的父节点,d[x]存储x到p[x]的距离
p = list(range(n))
d = [0] * n
# 返回x的祖宗节点
def find(x):
if p[x] != x:
t = find(p[x])
d[x] += d[p[x]]
p[x] = t
return p[x]
# 合并a和b所在的两个集合
p[find(a)] = find(b)
d[find(a)] = distance对于本题,记 m, n 分别为 grid 的行数和列数。
- 将所有走廊及 "0" 对应的格子与超级节点
m * n相连。 - 对于其它格子,判断其相邻(上、下、左、右)的格子是否为 "0" 或者与当前格子相同,若是,更新 size 并将两个格子相连。
- 最后,获取不与超级节点相连的格子的最大 size,即为答案。
class Solution:
def largestArea(self, grid: List[str]) -> int:
def find(x):
if p[x] != x:
p[x] = find(p[x])
return p[x]
m, n = len(grid), len(grid[0])
p = list(range(m * n + 1))
size = [1] * (m * n + 1)
dirs = [[0, -1], [0, 1], [1, 0], [-1, 0]]
for i in range(m):
for j in range(n):
if i == 0 or i == m - 1 or j == 0 or j == n - 1 or grid[i][j] == '0':
p[find(i * n + j)] = find(m * n)
else:
for a, b in dirs:
x, y = i + a, j + b
if (grid[x][y] == '0' or grid[i][j] == grid[x][y]) and find(
x * n + y
) != find(i * n + j):
size[find(x * n + y)] += size[find(i * n + j)]
p[find(i * n + j)] = find(x * n + y)
return max(
[
size[i * n + j]
for i in range(m)
for j in range(n)
if find(i * n + j) != find(m * n)
],
default=0,
)class Solution {
private int[] p;
public int largestArea(String[] grid) {
int m = grid.length;
int n = grid[0].length();
p = new int[m * n + 1];
int[] size = new int[m * n + 1];
for (int i = 0; i < p.length; ++i) {
p[i] = i;
size[i] = 1;
}
int[] dirs = {0, 1, 0, -1, 0};
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (i == 0 || i == m - 1 || j == 0 || j == n - 1 || grid[i].charAt(j) == '0') {
p[find(i * n + j)] = find(m * n);
} else {
for (int k = 0; k < 4; ++k) {
int x = i + dirs[k];
int y = j + dirs[k + 1];
if (grid[x].charAt(y) == '0' || grid[i].charAt(j) == grid[x].charAt(y)) {
if (find(x * n + y) != find(i * n + j)) {
size[find(x * n + y)] += size[find(i * n + j)];
p[find(i * n + j)] = find(x * n + y);
}
}
}
}
}
}
int ans = 0;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (find(i * n + j) != find(m * n)) {
ans = Math.max(ans, size[i * n + j]);
}
}
}
return ans;
}
private int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
}class Solution {
public:
vector<int> p;
int largestArea(vector<string>& grid) {
int m = grid.size(), n = grid[0].size();
p.resize(m * n + 1);
for (int i = 0; i < p.size(); ++i) p[i] = i;
vector<int> size(m * n + 1, 1);
vector<int> dirs = {-1, 0, 1, 0, -1};
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (i == 0 || i == m - 1 || j == 0 || j == n - 1 || grid[i][j] == '0')
p[find(i * n + j)] = find(m * n);
else {
for (int k = 0; k < 4; ++k) {
int x = i + dirs[k], y = j + dirs[k + 1];
if ((grid[x][y] == '0' || grid[i][j] == grid[x][y]) && find(x * n + y) != find(i * n + j)) {
size[find(x * n + y)] += size[find(i * n + j)];
p[find(i * n + j)] = find(x * n + y);
}
}
}
}
}
int ans = 0;
for (int i = 0; i < m; ++i)
for (int j = 0; j < n; ++j)
if (find(i * n + j) != find(m * n))
ans = max(ans, size[i * n + j]);
return ans;
}
int find(int x) {
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
};func largestArea(grid []string) int {
m, n := len(grid), len(grid[0])
p := make([]int, m*n+1)
size := make([]int, m*n+1)
for i := range p {
p[i] = i
size[i] = 1
}
dirs := []int{-1, 0, 1, 0, -1}
var find func(x int) int
find = func(x int) int {
if p[x] != x {
p[x] = find(p[x])
}
return p[x]
}
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
if i == 0 || i == m-1 || j == 0 || j == n-1 || grid[i][j] == '0' {
p[find(i*n+j)] = find(m * n)
} else {
for k := 0; k < 4; k++ {
x, y := i+dirs[k], j+dirs[k+1]
if (grid[x][y] == '0' || grid[i][j] == grid[x][y]) && find(x*n+y) != find(i*n+j) {
size[find(x*n+y)] += size[find(i*n+j)]
p[find(i*n+j)] = find(x*n + y)
}
}
}
}
}
ans := 0
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
if find(i*n+j) != find(m*n) && ans < size[i*n+j] {
ans = size[i*n+j]
}
}
}
return ans
}/**
* @param {string[]} grid
* @return {number}
*/
var largestArea = function (grid) {
const m = grid.length;
const n = grid[0].length;
let p = new Array(m * n + 1).fill(0);
let size = new Array(m * n + 1).fill(1);
for (let i = 0; i < p.length; ++i) {
p[i] = i;
}
const dirs = [-1, 0, 1, 0, -1];
function find(x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
if (i == 0 || i == m - 1 || j == 0 || j == n - 1 || grid[i][j] == '0') {
p[find(i * n + j)] = find(m * n);
} else {
for (let k = 0; k < 4; ++k) {
const x = i + dirs[k];
const y = j + dirs[k + 1];
if (
(grid[x][y] == '0' || grid[i][j] == grid[x][y]) &&
find(x * n + y) != find(i * n + j)
) {
size[find(x * n + y)] += size[find(i * n + j)];
p[find(i * n + j)] = find(x * n + y);
}
}
}
}
}
let ans = 0;
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
if (find(i * n + j) != find(m * n) && ans < size[i * n + j]) {
ans = size[i * n + j];
}
}
}
return ans;
};