Skip to content

Latest commit

 

History

History

1697.Checking Existence of Edge Length Limited Paths

Folders and files

NameName
Last commit message
Last commit date

parent directory

..
images
images
 
 
README.md
README.md
 
 
README_EN.md
README_EN.md
 
 
Solution.cpp
Solution.cpp
 
 
Solution.go
Solution.go
 
 
Solution.java
Solution.java
 
 
Solution.py
Solution.py
 
 
Solution.rs
Solution.rs
 
 

README.md

1697. 检查边长度限制的路径是否存在

English Version

题目描述

给你一个 n 个点组成的无向图边集 edgeList ，其中 edgeList[i] = [ui, vi, disi] 表示点 ui 和点 vi 之间有一条长度为 disi 的边。请注意，两个点之间可能有 超过一条边 。

给你一个查询数组queries ，其中 queries[j] = [pj, qj, limitj] ，你的任务是对于每个查询 queries[j] ，判断是否存在从 pj 到 qj 的路径，且这条路径上的每一条边都 严格小于 limitj 。

请你返回一个 布尔数组 answer ，其中 answer.length == queries.length ，当 queries[j] 的查询结果为 true 时， answer 第 j 个值为 true ，否则为 false 。

 

示例 1：

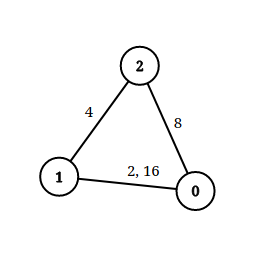
输入：n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
输出：[false,true]
解释：上图为给定的输入数据。注意到 0 和 1 之间有两条重边，分别为 2 和 16 。
对于第一个查询，0 和 1 之间没有小于 2 的边，所以我们返回 false 。
对于第二个查询，有一条路径（0 -> 1 -> 2）两条边都小于 5 ，所以这个查询我们返回 true 。

示例 2：

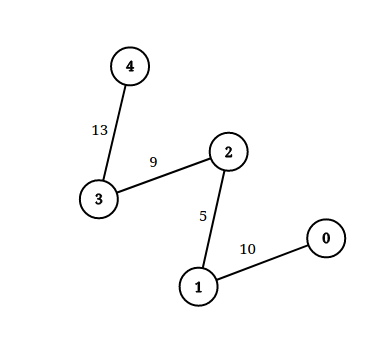
输入：n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]
输出：[true,false]
解释：上图为给定数据。

 

提示：

  • 2 <= n <= 105
  • 1 <= edgeList.length, queries.length <= 105
  • edgeList[i].length == 3
  • queries[j].length == 3
  • 0 <= ui, vi, pj, qj <= n - 1
  • ui != vi
  • pj != qj
  • 1 <= disi, limitj <= 109
  • 两个点之间可能有 多条 边。

解法

方法一：离线查询 + 并查集

根据题目要求，我们需要对每个查询 $queries[i]$ 进行判断，即判断当前查询的两个点 $a$ 和 $b$ 之间是否存在一条边权小于等于 $limit$ 的路径。

判断两点是否连通可以通过并查集来实现。另外，由于查询的顺序对结果没有影响，因此我们可以先将所有查询按照 $limit$ 从小到大排序，所有边也按照边权从小到大排序。

然后对于每个查询，我们从边权最小的边开始，将边权严格小于 $limit$ 的所有边加入并查集，接着利用并查集的查询操作判断两点是否连通即可。

时间复杂度 $O(m \times \log m + q \times \log q)$，其中 $m$ 和 $q$ 分别为边数和查询数。

class Solution:
    def distanceLimitedPathsExist(
        self, n: int, edgeList: List[List[int]], queries: List[List[int]]
    ) -> List[bool]:
        def find(x):
            if p[x] != x:
                p[x] = find(p[x])
            return p[x]

        p = list(range(n))
        edgeList.sort(key=lambda x: x[2])
        j = 0
        ans = [False] * len(queries)
        for i, (a, b, limit) in sorted(enumerate(queries), key=lambda x: x[1][2]):
            while j < len(edgeList) and edgeList[j][2] < limit:
                u, v, _ = edgeList[j]
                p[find(u)] = find(v)
                j += 1
            ans[i] = find(a) == find(b)
        return ans
class Solution {
    private int[] p;

    public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) {
        p = new int[n];
        for (int i = 0; i < n; ++i) {
            p[i] = i;
        }
        Arrays.sort(edgeList, (a, b) -> a[2] - b[2]);
        int m = queries.length;
        boolean[] ans = new boolean[m];
        Integer[] qid = new Integer[m];
        for (int i = 0; i < m; ++i) {
            qid[i] = i;
        }
        Arrays.sort(qid, (i, j) -> queries[i][2] - queries[j][2]);
        int j = 0;
        for (int i : qid) {
            int a = queries[i][0], b = queries[i][1], limit = queries[i][2];
            while (j < edgeList.length && edgeList[j][2] < limit) {
                int u = edgeList[j][0], v = edgeList[j][1];
                p[find(u)] = find(v);
                ++j;
            }
            ans[i] = find(a) == find(b);
        }
        return ans;
    }

    private int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }
}
class Solution {
public:
    vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {
        vector<int> p(n);
        iota(p.begin(), p.end(), 0);
        sort(edgeList.begin(), edgeList.end(), [](auto& a, auto& b) { return a[2] < b[2]; });
        function<int(int)> find = [&](int x) -> int {
            if (p[x] != x) p[x] = find(p[x]);
            return p[x];
        };
        int m = queries.size();
        vector<bool> ans(m);
        vector<int> qid(m);
        iota(qid.begin(), qid.end(), 0);
        sort(qid.begin(), qid.end(), [&](int i, int j) { return queries[i][2] < queries[j][2]; });
        int j = 0;
        for (int i : qid) {
            int a = queries[i][0], b = queries[i][1], limit = queries[i][2];
            while (j < edgeList.size() && edgeList[j][2] < limit) {
                int u = edgeList[j][0], v = edgeList[j][1];
                p[find(u)] = find(v);
                ++j;
            }
            ans[i] = find(a) == find(b);
        }
        return ans;
    }
};
func distanceLimitedPathsExist(n int, edgeList [][]int, queries [][]int) []bool {
	p := make([]int, n)
	for i := range p {
		p[i] = i
	}
	sort.Slice(edgeList, func(i, j int) bool { return edgeList[i][2] < edgeList[j][2] })
	var find func(int) int
	find = func(x int) int {
		if p[x] != x {
			p[x] = find(p[x])
		}
		return p[x]
	}
	m := len(queries)
	qid := make([]int, m)
	ans := make([]bool, m)
	for i := range qid {
		qid[i] = i
	}
	sort.Slice(qid, func(i, j int) bool { return queries[qid[i]][2] < queries[qid[j]][2] })
	j := 0
	for _, i := range qid {
		a, b, limit := queries[i][0], queries[i][1], queries[i][2]
		for j < len(edgeList) && edgeList[j][2] < limit {
			u, v := edgeList[j][0], edgeList[j][1]
			p[find(u)] = find(v)
			j++
		}
		ans[i] = find(a) == find(b)
	}
	return ans
}
impl Solution {
    #[allow(dead_code)]
    pub fn distance_limited_paths_exist(
        n: i32,
        edge_list: Vec<Vec<i32>>,
        queries: Vec<Vec<i32>>
    ) -> Vec<bool> {
        let mut disjoint_set: Vec<usize> = vec![0; n as usize];
        let mut ans_vec: Vec<bool> = vec![false; queries.len()];
        let mut q_vec: Vec<usize> = vec![0; queries.len()];

        // Initialize the set
        for i in 0..n {
            disjoint_set[i as usize] = i as usize;
        }

        // Initialize the q_vec
        for i in 0..queries.len() {
            q_vec[i] = i;
        }

        // Sort the q_vec based on the query limit, from the lowest to highest
        q_vec.sort_by(|i, j| queries[*i][2].cmp(&queries[*j][2]));

        // Sort the edge_list based on the edge weight, from the lowest to highest
        let mut edge_list = edge_list.clone();
        edge_list.sort_by(|i, j| i[2].cmp(&j[2]));

        let mut edge_idx: usize = 0;
        for q_idx in &q_vec {
            let s = queries[*q_idx][0] as usize;
            let d = queries[*q_idx][1] as usize;
            let limit = queries[*q_idx][2];
            // Construct the disjoint set
            while edge_idx < edge_list.len() && edge_list[edge_idx][2] < limit {
                Solution::union(
                    edge_list[edge_idx][0] as usize,
                    edge_list[edge_idx][1] as usize,
                    &mut disjoint_set
                );
                edge_idx += 1;
            }
            // If the parents of s & d are the same, this query should be `true`
            // Otherwise, the current query is `false`
            ans_vec[*q_idx] = Solution::check_valid(s, d, &mut disjoint_set);
        }

        ans_vec
    }

    #[allow(dead_code)]
    pub fn find(x: usize, d_set: &mut Vec<usize>) -> usize {
        if d_set[x] != x {
            d_set[x] = Solution::find(d_set[x], d_set);
        }
        return d_set[x];
    }

    #[allow(dead_code)]
    pub fn union(s: usize, d: usize, d_set: &mut Vec<usize>) {
        let p_s = Solution::find(s, d_set);
        let p_d = Solution::find(d, d_set);
        d_set[p_s] = p_d;
    }

    #[allow(dead_code)]
    pub fn check_valid(s: usize, d: usize, d_set: &mut Vec<usize>) -> bool {
        let p_s = Solution::find(s, d_set);
        let p_d = Solution::find(d, d_set);
        p_s == p_d
    }
}

附并查集相关介绍以及常用模板：

并查集是一种树形的数据结构，顾名思义，它用于处理一些不交集的合并及查询问题。 它支持两种操作：

  1. 查找（Find）：确定某个元素处于哪个子集，单次操作时间复杂度 $O(\alpha(n))$
  2. 合并（Union）：将两个子集合并成一个集合，单次操作时间复杂度 $O(\alpha(n))$

其中 $\alpha$ 为阿克曼函数的反函数，其增长极其缓慢，也就是说其单次操作的平均运行时间可以认为是一个很小的常数。

以下是并查集的常用模板，需要熟练掌握。其中：

  • n 表示节点数
  • p 存储每个点的父节点，初始时每个点的父节点都是自己
  • size 只有当节点是祖宗节点时才有意义，表示祖宗节点所在集合中，点的数量
  • find(x) 函数用于查找 $x$ 所在集合的祖宗节点
  • union(a, b) 函数用于合并 $a$ 和 $b$ 所在的集合
p = list(range(n))
size = [1] * n

def find(x):
    if p[x] != x:
        # 路径压缩
        p[x] = find(p[x])
    return p[x]


def union(a, b):
    pa, pb = find(a), find(b)
    if pa == pb:
        return
    p[pa] = pb
    size[pb] += size[pa]
int[] p = new int[n];
int[] size = new int[n];
for (int i = 0; i < n; ++i) {
    p[i] = i;
    size[i] = 1;
}

int find(int x) {
    if (p[x] != x) {
        // 路径压缩
        p[x] = find(p[x]);
    }
    return p[x];
}

void union(int a, int b) {
    int pa = find(a), pb = find(b);
    if (pa == pb) {
        return;
    }
    p[pa] = pb;
    size[pb] += size[pa];
}
vector<int> p(n);
iota(p.begin(), p.end(), 0);
vector<int> size(n, 1);

int find(int x) {
    if (p[x] != x) {
        // 路径压缩
        p[x] = find(p[x]);
    }
    return p[x];
}

void unite(int a, int b) {
    int pa = find(a), pb = find(b);
    if (pa == pb) return;
    p[pa] = pb;
    size[pb] += size[pa];
}
p := make([]int, n)
size := make([]int, n)
for i := range p {
    p[i] = i
    size[i] = 1
}

func find(x int) int {
    if p[x] != x {
        // 路径压缩
        p[x] = find(p[x])
    }
    return p[x]
}

func union(a, b int) {
    pa, pb := find(a), find(b)
    if pa == pb {
        return
    }
    p[pa] = pb
    size[pb] += size[pa]
}