comments	difficulty	edit_url	tags
true	中等	https://github.com/doocs/leetcode/edit/main/solution/0300-0399/0304.Range%20Sum%20Query%202D%20-%20Immutable/README.md	设计 数组 矩阵 前缀和

304. 二维区域和检索 - 矩阵不可变

English Version

题目描述

给定一个二维矩阵 matrix，以下类型的多个请求：

• 计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。

实现 NumMatrix 类：

• NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
• int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素 总和 。

 

示例 1：

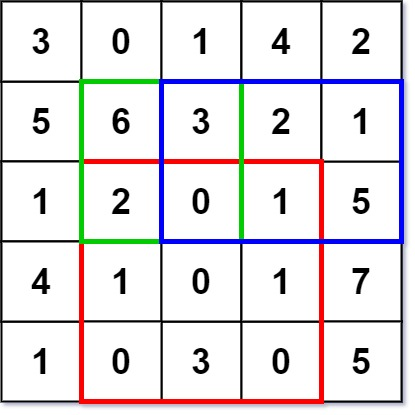
输入: 
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出: 
[null, 8, 11, 12]

解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

 

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• -105 <= matrix[i][j] <= 105
• 0 <= row1 <= row2 < m
• 0 <= col1 <= col2 < n
• 最多调用 104 次 sumRegion 方法

解法

方法一：二维前缀和

我们用 $s[i+1][j+1]$ 表示第 $i$ 行第 $j$ 列左上部分所有元素之和，下标 $i$ 和 $j$ 均从 $0$ 开始。可以得到以下前缀和公式：

$$s[i+1][j+1]=s[i+1][j]+s[i][j+1]-s[i][j]+nums[i][j]$$

那么分别以 $(x_1,y_1)$ 和 $(x_2,y_2)$ 为左上角和右下角的矩形的元素之和为：

$$s[x_2+1][y_2+1]-s[x_2+1][y_1]-s[x_1][y_2+1]+s[x_1][y_1]$$

我们在初始化方法中预处理出前缀和数组 $s$，在查询方法中直接返回上述公式的结果即可。

初始化的时间复杂度为 $O(m\times n)$，查询的时间复杂度为 $O(1)$。空间复杂度为 $O(m\times n)$。

Python3

class NumMatrix:
    def __init__(self, matrix: List[List[int]]):
        m, n = len(matrix), len(matrix[0])
        self.s = [[0] * (n + 1) for _ in range(m + 1)]
        for i, row in enumerate(matrix):
            for j, v in enumerate(row):
                self.s[i + 1][j + 1] = (
                    self.s[i][j + 1] + self.s[i + 1][j] - self.s[i][j] + v
                )

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        return (
            self.s[row2 + 1][col2 + 1]
            - self.s[row2 + 1][col1]
            - self.s[row1][col2 + 1]
            + self.s[row1][col1]
        )


# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# param_1 = obj.sumRegion(row1,col1,row2,col2)

Java

class NumMatrix {
    private int[][] s;

    public NumMatrix(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        s = new int[m + 1][n + 1];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + matrix[i][j];
            }
        }
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        return s[row2 + 1][col2 + 1] - s[row2 + 1][col1] - s[row1][col2 + 1] + s[row1][col1];
    }
}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix obj = new NumMatrix(matrix);
 * int param_1 = obj.sumRegion(row1,col1,row2,col2);
 */

C++

class NumMatrix {
public:
    vector<vector<int>> s;

    NumMatrix(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        s.resize(m + 1, vector<int>(n + 1));
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + matrix[i][j];
            }
        }
    }

    int sumRegion(int row1, int col1, int row2, int col2) {
        return s[row2 + 1][col2 + 1] - s[row2 + 1][col1] - s[row1][col2 + 1] + s[row1][col1];
    }
};

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix* obj = new NumMatrix(matrix);
 * int param_1 = obj->sumRegion(row1,col1,row2,col2);
 */

Go

type NumMatrix struct {
	s [][]int
}

func Constructor(matrix [][]int) NumMatrix {
	m, n := len(matrix), len(matrix[0])
	s := make([][]int, m+1)
	for i := range s {
		s[i] = make([]int, n+1)
	}
	for i, row := range matrix {
		for j, v := range row {
			s[i+1][j+1] = s[i+1][j] + s[i][j+1] - s[i][j] + v
		}
	}
	return NumMatrix{s}
}

func (this *NumMatrix) SumRegion(row1 int, col1 int, row2 int, col2 int) int {
	return this.s[row2+1][col2+1] - this.s[row2+1][col1] - this.s[row1][col2+1] + this.s[row1][col1]
}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * obj := Constructor(matrix);
 * param_1 := obj.SumRegion(row1,col1,row2,col2);
 */

TypeScript

class NumMatrix {
    private s: number[][];

    constructor(matrix: number[][]) {
        const m = matrix.length;
        const n = matrix[0].length;
        this.s = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));
        for (let i = 0; i < m; ++i) {
            for (let j = 0; j < n; ++j) {
                this.s[i + 1][j + 1] =
                    this.s[i + 1][j] + this.s[i][j + 1] - this.s[i][j] + matrix[i][j];
            }
        }
    }

    sumRegion(row1: number, col1: number, row2: number, col2: number): number {
        return (
            this.s[row2 + 1][col2 + 1] -
            this.s[row2 + 1][col1] -
            this.s[row1][col2 + 1] +
            this.s[row1][col1]
        );
    }
}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * var obj = new NumMatrix(matrix)
 * var param_1 = obj.sumRegion(row1,col1,row2,col2)
 */

Rust

/**
 * Your NumMatrix object will be instantiated and called as such:
 * let obj = NumMatrix::new(matrix);
 * let ret_1: i32 = obj.sum_region(row1, col1, row2, col2);
 */

struct NumMatrix {
    // Of size (N + 1) * (M + 1)
    prefix_vec: Vec<Vec<i32>>,
    n: usize,
    m: usize,
    is_initialized: bool,
    ref_vec: Vec<Vec<i32>>,
}

/**
 * `&self` means the method takes an immutable reference.
 * If you need a mutable reference, change it to `&mut self` instead.
 */
impl NumMatrix {
    fn new(matrix: Vec<Vec<i32>>) -> Self {
        NumMatrix {
            prefix_vec: vec![vec![0; matrix[0].len() + 1]; matrix.len() + 1],
            n: matrix.len(),
            m: matrix[0].len(),
            is_initialized: false,
            ref_vec: matrix,
        }
    }

    fn sum_region(&mut self, row1: i32, col1: i32, row2: i32, col2: i32) -> i32 {
        if !self.is_initialized {
            self.initialize_prefix_vec();
        }
        // Since i32 will let `rustc` complain, just make it happy
        let row1: usize = row1 as usize;
        let col1: usize = col1 as usize;
        let row2: usize = row2 as usize;
        let col2: usize = col2 as usize;
        // Return the value in O(1)
        self.prefix_vec[row2 + 1][col2 + 1]
            - self.prefix_vec[row2 + 1][col1]
            - self.prefix_vec[row1][col2 + 1]
            + self.prefix_vec[row1][col1]
    }

    fn initialize_prefix_vec(&mut self) {
        // Initialize the prefix sum vector
        for i in 0..self.n {
            for j in 0..self.m {
                self.prefix_vec[i + 1][j + 1] =
                    self.prefix_vec[i][j + 1] + self.prefix_vec[i + 1][j] - self.prefix_vec[i][j]
                        + self.ref_vec[i][j];
            }
        }
        self.is_initialized = true;
    }
}

JavaScript

/**
 * @param {number[][]} matrix
 */
var NumMatrix = function (matrix) {
    const m = matrix.length;
    const n = matrix[0].length;
    this.s = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            this.s[i + 1][j + 1] =
                this.s[i + 1][j] + this.s[i][j + 1] - this.s[i][j] + matrix[i][j];
        }
    }
};

/**
 * @param {number} row1
 * @param {number} col1
 * @param {number} row2
 * @param {number} col2
 * @return {number}
 */
NumMatrix.prototype.sumRegion = function (row1, col1, row2, col2) {
    return (
        this.s[row2 + 1][col2 + 1] -
        this.s[row2 + 1][col1] -
        this.s[row1][col2 + 1] +
        this.s[row1][col1]
    );
};

/**
 * Your NumMatrix object will be instantiated and called as such:
 * var obj = new NumMatrix(matrix)
 * var param_1 = obj.sumRegion(row1,col1,row2,col2)
 */

Kotlin

class NumMatrix(matrix: Array<IntArray>) {
    private val n: Int
    private val m: Int
    private val matrix: Array<IntArray>
    private val prefix_sums_matrix: Array<IntArray>
    private var initialized: Boolean

    init {
        this.n = matrix.size
        this.m = matrix[0].size
        this.matrix = matrix
        this.prefix_sums_matrix = Array(n + 1) { IntArray(m + 1) }
        this.initialized = false
    }

    fun sumRegion(row1: Int, col1: Int, row2: Int, col2: Int): Int {
        this.init()
        return this.prefix_sums_matrix[row2 + 1][col2 + 1] -
            this.prefix_sums_matrix[row2 + 1][col1] -
            this.prefix_sums_matrix[row1][col2 + 1] +
            this.prefix_sums_matrix[row1][col1]
    }

    private fun init(): Boolean {
        if (!this.initialized) {
            for (i in 0..<this.n) {
                for (j in 0..<this.m) {
                    this.prefix_sums_matrix[i + 1][j + 1] =
                        this.prefix_sums_matrix[i + 1][j] +
                        this.prefix_sums_matrix[i][j + 1] -
                        this.prefix_sums_matrix[i][j] +
                        this.matrix[i][j]
                }
            }
            this.initialized = true
            return true
        }
        return false
    }
}

/**
 * Your NumMatrix object will be instantiated and called as such: var obj = NumMatrix(matrix) var
 * param_1 = obj.sumRegion(row1,col1,row2,col2)
 */