1104. 二叉树寻路

English Version

题目描述

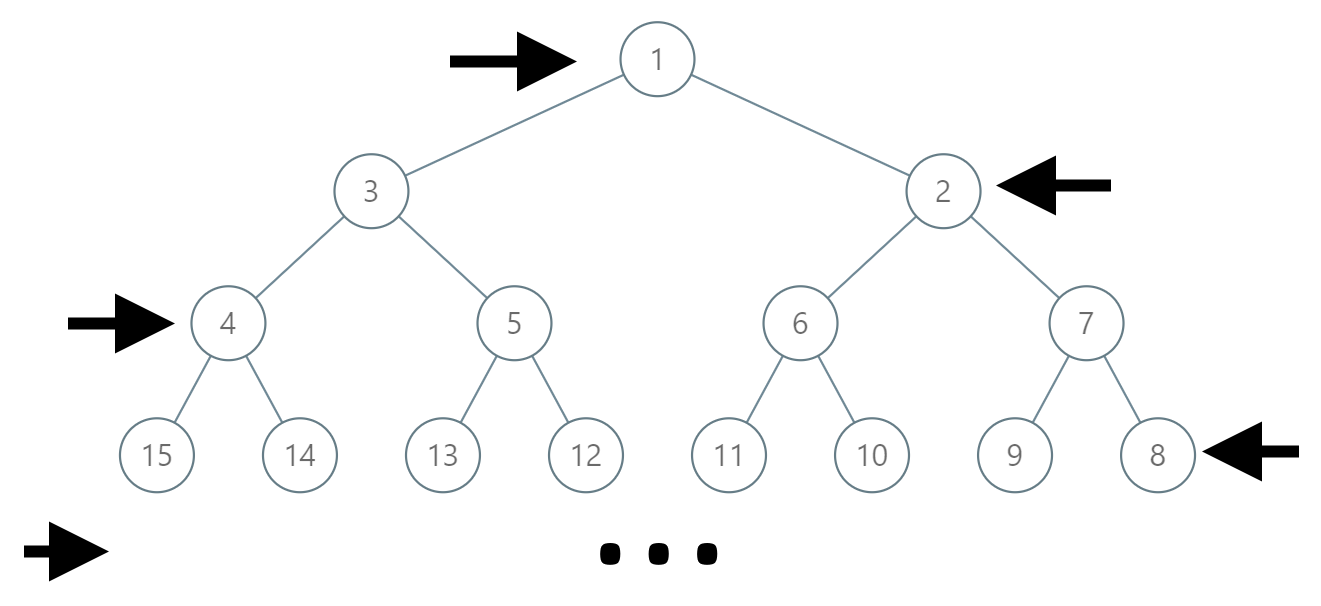
在一棵无限的二叉树上，每个节点都有两个子节点，树中的节点 逐行 依次按 “之” 字形进行标记。

如下图所示，在奇数行（即，第一行、第三行、第五行……）中，按从左到右的顺序进行标记；

而偶数行（即，第二行、第四行、第六行……）中，按从右到左的顺序进行标记。

给你树上某一个节点的标号 label，请你返回从根节点到该标号为 label 节点的路径，该路径是由途经的节点标号所组成的。

 

示例 1：

输入：label = 14
输出：[1,3,4,14]

示例 2：

输入：label = 26
输出：[1,2,6,10,26]

 

提示：

• 1 <= label <= 10^6

解法

方法一：数学

对于一棵完全二叉树，第 $i$ 行的节点个数为 $2^{i-1}$，第 $i$ 行的节点编号范围为 $[2^{i-1}, 2^i - 1]$。而题目中对于奇数行，按从左到右的顺序进行标记，对于偶数行，按从右到左的顺序进行标记。所以对于第 $i$ 行的节点 $label$，它的互补节点编号为 $2^{i-1} + 2^i - 1 - label$。所以节点 $label$ 的实际父节点编号为 $(2^{i-1} + 2^i - 1 - label) / 2$。我们可以通过不断地求互补节点编号和父节点编号，直到到达根节点，即可得到从根节点到节点 $label$ 的路径。

最后，我们需要将路径反转，因为题目要求路径是从根节点到节点 $label$ 的路径。

时间复杂度 $O(\log n)$，其中 $n$ 为节点 $label$ 的编号。忽略答案的空间消耗，空间复杂度 $O(1)$。

class Solution:
    def pathInZigZagTree(self, label: int) -> List[int]:
        x = i = 1
        while (x << 1) <= label:
            x <<= 1
            i += 1
        ans = [0] * i
        while i:
            ans[i - 1] = label
            label = ((1 << (i - 1)) + (1 << i) - 1 - label) >> 1
            i -= 1
        return ans

class Solution {
    public List<Integer> pathInZigZagTree(int label) {
        int x = 1, i = 1;
        while ((x << 1) <= label) {
            x <<= 1;
            ++i;
        }
        List<Integer> ans = new ArrayList<>();
        for (; i > 0; --i) {
            ans.add(label);
            label = ((1 << (i - 1)) + (1 << i) - 1 - label) >> 1;
        }
        Collections.reverse(ans);
        return ans;
    }
}

class Solution {
public:
    vector<int> pathInZigZagTree(int label) {
        int x = 1, i = 1;
        while ((x << 1) <= label) {
            x <<= 1;
            ++i;
        }
        vector<int> ans;
        for (; i > 0; --i) {
            ans.push_back(label);
            label = ((1 << (i - 1)) + (1 << i) - 1 - label) >> 1;
        }
        reverse(ans.begin(), ans.end());
        return ans;
    }
};

func pathInZigZagTree(label int) (ans []int) {
	x, i := 1, 1
	for x<<1 <= label {
		x <<= 1
		i++
	}
	for ; i > 0; i-- {
		ans = append(ans, label)
		label = ((1 << (i - 1)) + (1 << i) - 1 - label) >> 1
	}
	for i, j := 0, len(ans)-1; i < j; i, j = i+1, j-1 {
		ans[i], ans[j] = ans[j], ans[i]
	}
	return
}