668. 乘法表中第 k 小的数

English Version

题目描述

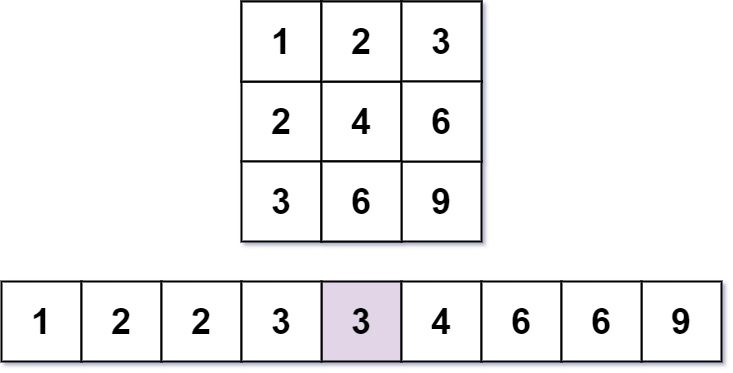
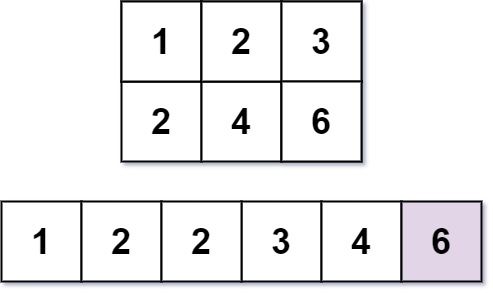
几乎每一个人都用 乘法表。但是你能在乘法表中快速找到第 k 小的数字吗？

乘法表是大小为 m x n 的一个整数矩阵，其中 mat[i][j] == i * j（下标从 1 开始）。

给你三个整数 m、n 和 k，请你在大小为 m x n 的乘法表中，找出并返回第 k 小的数字。

 

示例 1：

输入：m = 3, n = 3, k = 5
输出：3
解释：第 5 小的数字是 3 。

示例 2：

输入：m = 2, n = 3, k = 6
输出：6
解释：第 6 小的数字是 6 。

 

提示：

• 1 <= m, n <= 3 * 104
• 1 <= k <= m * n

解法

方法一：二分查找

题目可以转换为，求有多少个数不超过 x。对于每一行 i，所有数都是 i 的倍数，不超过 x 的个数有 x / i 个。

二分枚举 x，累加每一行不超过 x 的个数，得到 cnt。找到 cnt >= k 的最小 x。

class Solution:
    def findKthNumber(self, m: int, n: int, k: int) -> int:
        left, right = 1, m * n
        while left < right:
            mid = (left + right) >> 1
            cnt = 0
            for i in range(1, m + 1):
                cnt += min(mid // i, n)
            if cnt >= k:
                right = mid
            else:
                left = mid + 1
        return left

class Solution {
    public int findKthNumber(int m, int n, int k) {
        int left = 1, right = m * n;
        while (left < right) {
            int mid = (left + right) >>> 1;
            int cnt = 0;
            for (int i = 1; i <= m; ++i) {
                cnt += Math.min(mid / i, n);
            }
            if (cnt >= k) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }
}

class Solution {
public:
    int findKthNumber(int m, int n, int k) {
        int left = 1, right = m * n;
        while (left < right) {
            int mid = (left + right) >> 1;
            int cnt = 0;
            for (int i = 1; i <= m; ++i) cnt += min(mid / i, n);
            if (cnt >= k)
                right = mid;
            else
                left = mid + 1;
        }
        return left;
    }
};

func findKthNumber(m int, n int, k int) int {
	left, right := 1, m*n
	for left < right {
		mid := (left + right) >> 1
		cnt := 0
		for i := 1; i <= m; i++ {
			cnt += min(mid/i, n)
		}
		if cnt >= k {
			right = mid
		} else {
			left = mid + 1
		}
	}
	return left
}