comments	difficulty	edit_url	tags
true	中等	https://github.com/doocs/leetcode/edit/main/solution/0200-0299/0236.Lowest%20Common%20Ancestor%20of%20a%20Binary%20Tree/README.md	树 深度优先搜索 二叉树

236. 二叉树的最近公共祖先

English Version

题目描述

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

 

示例 1：

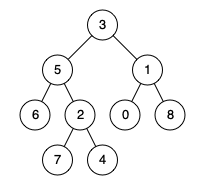
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

 

提示：

• 树中节点数目在范围 [2, 105] 内。
• -109 <= Node.val <= 109
• 所有 Node.val 互不相同 。
• p != q
• p 和 q 均存在于给定的二叉树中。

解法

方法一：递归

我们递归遍历二叉树：

如果当前节点为空或者等于 $p$ 或者 $q$，则返回当前节点；

否则，我们递归遍历左右子树，将返回的结果分别记为 $left$ 和 $right$。如果 $left$ 和 $right$ 都不为空，则说明 $p$ 和 $q$ 分别在左右子树中，因此当前节点即为最近公共祖先；如果 $left$ 和 $right$ 中只有一个不为空，返回不为空的那个。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 为二叉树节点个数。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None


class Solution:
    def lowestCommonAncestor(
        self, root: "TreeNode", p: "TreeNode", q: "TreeNode"
    ) -> "TreeNode":
        if root in (None, p, q):
            return root
        left = self.lowestCommonAncestor(root.left, p, q)
        right = self.lowestCommonAncestor(root.right, p, q)
        return root if left and right else (left or right)

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null || root == p || root == q) {
            return root;
        }
        var left = lowestCommonAncestor(root.left, p, q);
        var right = lowestCommonAncestor(root.right, p, q);
        if (left != null && right != null) {
            return root;
        }
        return left == null ? right : left;
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == nullptr || root == p || root == q) {
            return root;
        }
        auto left = lowestCommonAncestor(root->left, p, q);
        auto right = lowestCommonAncestor(root->right, p, q);
        if (left && right) {
            return root;
        }
        return left ? left : right;
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
	if root == nil || root == p || root == q {
		return root
	}
	left := lowestCommonAncestor(root.Left, p, q)
	right := lowestCommonAncestor(root.Right, p, q)
	if left != nil && right != nil {
		return root
	}
	if left != nil {
		return left
	}
	return right
}

TypeScript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function lowestCommonAncestor(
    root: TreeNode | null,
    p: TreeNode | null,
    q: TreeNode | null,
): TreeNode | null {
    if (!root || root === p || root === q) {
        return root;
    }
    const left = lowestCommonAncestor(root.left, p, q);
    const right = lowestCommonAncestor(root.right, p, q);
    return left && right ? root : left || right;
}

Rust

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
    pub fn lowest_common_ancestor(
        root: Option<Rc<RefCell<TreeNode>>>,
        p: Option<Rc<RefCell<TreeNode>>>,
        q: Option<Rc<RefCell<TreeNode>>>,
    ) -> Option<Rc<RefCell<TreeNode>>> {
        if root.is_none() || root == p || root == q {
            return root;
        }
        let left = Self::lowest_common_ancestor(
            root.as_ref().unwrap().borrow().left.clone(),
            p.clone(),
            q.clone(),
        );
        let right = Self::lowest_common_ancestor(
            root.as_ref().unwrap().borrow().right.clone(),
            p.clone(),
            q.clone(),
        );
        if left.is_some() && right.is_some() {
            return root;
        }
        if left.is_none() {
            return right;
        }
        return left;
    }
}

JavaScript

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {TreeNode}
 */
var lowestCommonAncestor = function (root, p, q) {
    if (!root || root === p || root === q) {
        return root;
    }
    const left = lowestCommonAncestor(root.left, p, q);
    const right = lowestCommonAncestor(root.right, p, q);
    return left && right ? root : left || right;
};