743. 网络延迟时间

English Version

题目描述

有 n 个网络节点，标记为 1 到 n。

给你一个列表 times，表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi)，其中 ui 是源节点，vi 是目标节点， wi 是一个信号从源节点传递到目标节点的时间。

现在，从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1 。

 

示例 1：

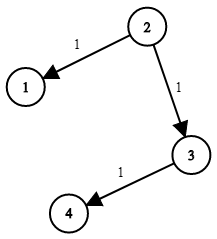
输入：times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
输出：2

示例 2：

输入：times = [[1,2,1]], n = 2, k = 1
输出：1

示例 3：

输入：times = [[1,2,1]], n = 2, k = 2
输出：-1

 

提示：

• 1 <= k <= n <= 100
• 1 <= times.length <= 6000
• times[i].length == 3
• 1 <= ui, vi <= n
• ui != vi
• 0 <= wi <= 100
• 所有 (ui, vi) 对都 互不相同（即，不含重复边）

解法

方法一：朴素 Dijkstra 算法

Python3

class Solution:
    def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
        N = 110
        INF = 0x3f3f
        g = [[INF] * N for _ in range(N)]
        for u, v, w in times:
            g[u][v] = w
        dist = [INF] * N
        dist[k] = 0
        vis = [False] * N
        for i in range(n):
            t = -1
            for j in range(1, n + 1):
                if not vis[j] and (t == -1 or dist[t] > dist[j]):
                    t = j
            vis[t] = True
            for j in range(1, n + 1):
                dist[j] = min(dist[j], dist[t] + g[t][j])

        ans = max(dist[1: n + 1])
        return -1 if ans == INF else ans

Java

class Solution {
    private static final int N = 110;
    private static final int INF = 0x3f3f;

    public int networkDelayTime(int[][] times, int n, int k) {
        int[][] g = new int[N][N];
        for (int i = 0; i < N; ++i) {
            Arrays.fill(g[i], INF);
        }
        for (int[] e : times) {
            g[e[0]][e[1]] = e[2];
        }
        int[] dist = new int[N];
        Arrays.fill(dist, INF);
        dist[k] = 0;
        boolean[] vis = new boolean[N];
        for (int i = 0; i < n; ++i) {
            int t = -1;
            for (int j = 1; j <= n; ++j) {
                if (!vis[j] && (t == -1 || dist[t] > dist[j])) {
                    t = j;
                }
            }
            vis[t] = true;
            for (int j = 1; j <= n; ++j) {
                dist[j] = Math.min(dist[j], dist[t] + g[t][j]);
            }
        }
        int ans = 0;
        for (int i = 1; i <= n; ++i) {
            ans = Math.max(ans, dist[i]);
        }
        return ans == INF ? -1 : ans;
    }
}

Go

const Inf = 0x3f3f3f3f

type pair struct {
	first  int
	second int
}

var _ heap.Interface = (*pairs)(nil)

type pairs []pair

func (a pairs) Len() int { return len(a) }
func (a pairs) Less(i int, j int) bool {
	return a[i].first < a[j].first || a[i].first == a[j].first && a[i].second < a[j].second
}
func (a pairs) Swap(i int, j int)   { a[i], a[j] = a[j], a[i] }
func (a *pairs) Push(x interface{}) { *a = append(*a, x.(pair)) }
func (a *pairs) Pop() interface{}   { l := len(*a); t := (*a)[l-1]; *a = (*a)[:l-1]; return t }

func networkDelayTime(times [][]int, n int, k int) int {
	graph := make([]pairs, n)
	for _, time := range times {
		from, to, time := time[0]-1, time[1]-1, time[2]
		graph[from] = append(graph[from], pair{to, time})
	}

	dis := make([]int, n)
	for i := range dis {
		dis[i] = Inf
	}
	dis[k-1] = 0

	vis := make([]bool, n)
	h := make(pairs, 0)
	heap.Push(&h, pair{0, k - 1})
	for len(h) > 0 {
		from := heap.Pop(&h).(pair).second
		if vis[from] {
			continue
		}
		vis[from] = true
		for _, e := range graph[from] {
			to, d := e.first, dis[from]+e.second
			if d < dis[to] {
				dis[to] = d
				heap.Push(&h, pair{d, to})
			}
		}
	}

	ans := math.MinInt32
	for _, d := range dis {
		ans = max(ans, d)
	}
	if ans == Inf {
		return -1
	}
	return ans
}

func max(x, y int) int {
	if x > y {
		return x
	}
	return y
}

C++

class Solution {
public:
    int N = 110;
    int INF = 0x3f3f;

    int networkDelayTime(vector<vector<int>>& times, int n, int k) {
        vector<vector<int>> g(N, vector<int>(N, INF));
        for (auto& e : times) g[e[0]][e[1]] = e[2];
        vector<int> dist(N, INF);
        dist[k] = 0;
        vector<bool> vis(N);
        for (int i = 0; i < n; ++i)
        {
            int t = -1;
            for (int j = 1; j <= n; ++j)
            {
                if (!vis[j] && (t == -1 || dist[t] > dist[j]))
                {
                    t = j;
                }
            }
            vis[t] = true;
            for (int j = 1; j <= n; ++j)
            {
                dist[j] = min(dist[j], dist[t] + g[t][j]);
            }
        }
        int ans = *max_element(dist.begin() + 1, dist.begin() + 1 + n);
        return ans == INF ? -1 : ans;
    }
};

...