Name	Name	Last commit message	Last commit date
parent directory ..
images	images
README.md	README.md
README_EN.md	README_EN.md
Solution.cpp	Solution.cpp
Solution.go	Solution.go
Solution.java	Solution.java
Solution.py	Solution.py
Solution.ts	Solution.ts

2385. 感染二叉树需要的总时间

题目描述

给你一棵二叉树的根节点 root ，二叉树中节点的值 互不相同 。另给你一个整数 start 。在第 0 分钟，感染将会从值为 start 的节点开始爆发。

每分钟，如果节点满足以下全部条件，就会被感染：

节点此前还没有感染。
节点与一个已感染节点相邻。

返回感染整棵树需要的分钟数。

示例 1：

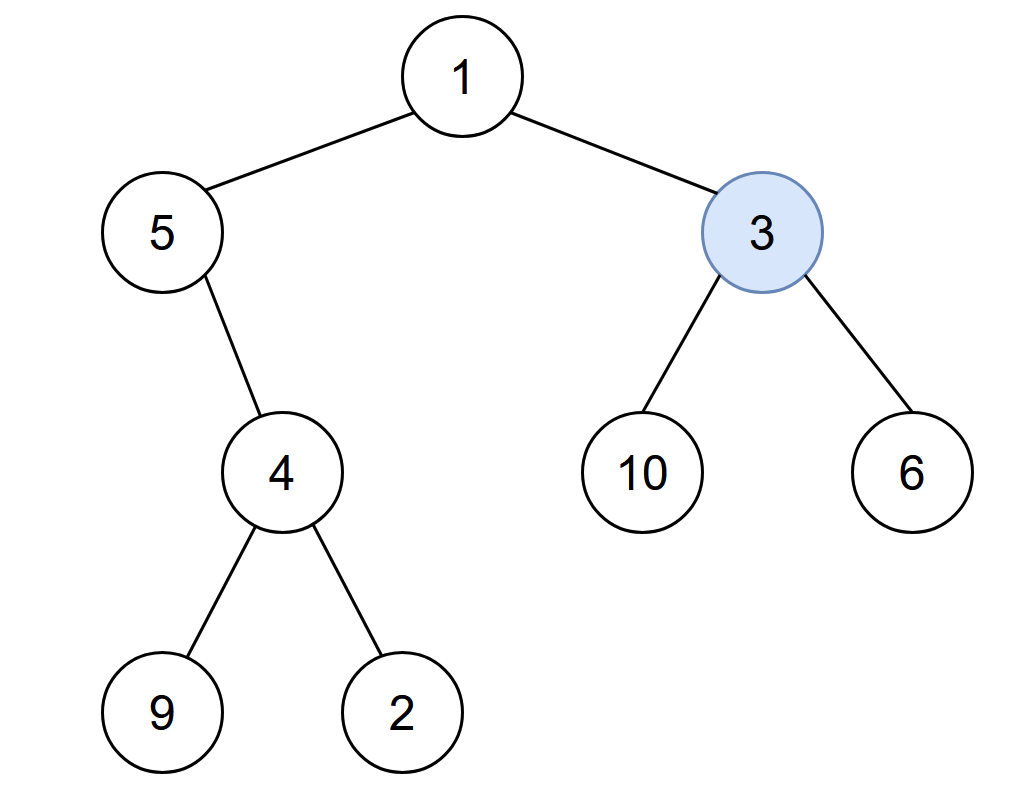
输入：root = [1,5,3,null,4,10,6,9,2], start = 3
输出：4
解释：节点按以下过程被感染：
- 第 0 分钟：节点 3
- 第 1 分钟：节点 1、10、6
- 第 2 分钟：节点5
- 第 3 分钟：节点 4
- 第 4 分钟：节点 9 和 2
感染整棵树需要 4 分钟，所以返回 4 。

示例 2：

输入：root = [1], start = 1
输出：0
解释：第 0 分钟，树中唯一一个节点处于感染状态，返回 0 。

提示：

树中节点的数目在范围 [1, 10⁵] 内
1 <= Node.val <= 10⁵
每个节点的值 互不相同
树中必定存在值为 start 的节点

解法

方法一：DFS + BFS

先通过 $DFS$ 建图，得到 $g$。然后以 $start$ 作为起点，哈希表 $vis$ 标记访问过的节点，通过 $BFS$ 以及前面得到的图 $g$，逐层往外扩展，扩展的次数即为答案。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 为二叉树的节点个数。

方法二：两次 DFS

与方法一一样，我们先通过 $DFS$ 建图，得到 $g$。然后以 $start$ 作为起点，通过 $DFS$ 搜索整棵树，找到最远距离，即为答案。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 为二叉树的节点个数。

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def amountOfTime(self, root: Optional[TreeNode], start: int) -> int:
        def dfs(root):
            if root is None:
                return
            if root.left:
                g[root.val].append(root.left.val)
                g[root.left.val].append(root.val)
            if root.right:
                g[root.val].append(root.right.val)
                g[root.right.val].append(root.val)
            dfs(root.left)
            dfs(root.right)

        g = defaultdict(list)
        dfs(root)
        vis = set()
        q = deque([start])
        ans = -1
        while q:
            ans += 1
            for _ in range(len(q)):
                i = q.popleft()
                vis.add(i)
                for j in g[i]:
                    if j not in vis:
                        q.append(j)
        return ans

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def amountOfTime(self, root: Optional[TreeNode], start: int) -> int:
        def dfs(root):
            if root is None:
                return
            if root.left:
                g[root.val].append(root.left.val)
                g[root.left.val].append(root.val)
            if root.right:
                g[root.val].append(root.right.val)
                g[root.right.val].append(root.val)
            dfs(root.left)
            dfs(root.right)

        def dfs2(i, fa):
            ans = 0
            for j in g[i]:
                if j != fa:
                    ans = max(ans, 1 + dfs2(j, i))
            return ans

        g = defaultdict(list)
        dfs(root)
        return dfs2(start, -1)

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private Map<Integer, List<Integer>> g = new HashMap<>();

    public int amountOfTime(TreeNode root, int start) {
        dfs(root);
        Deque<Integer> q = new ArrayDeque<>();
        Set<Integer> vis = new HashSet<>();
        q.offer(start);
        int ans = -1;
        while (!q.isEmpty()) {
            ++ans;
            for (int n = q.size(); n > 0; --n) {
                int i = q.pollFirst();
                vis.add(i);
                if (g.containsKey(i)) {
                    for (int j : g.get(i)) {
                        if (!vis.contains(j)) {
                            q.offer(j);
                        }
                    }
                }
            }
        }
        return ans;
    }

    private void dfs(TreeNode root) {
        if (root == null) {
            return;
        }
        if (root.left != null) {
            g.computeIfAbsent(root.val, k -> new ArrayList<>()).add(root.left.val);
            g.computeIfAbsent(root.left.val, k -> new ArrayList<>()).add(root.val);
        }
        if (root.right != null) {
            g.computeIfAbsent(root.val, k -> new ArrayList<>()).add(root.right.val);
            g.computeIfAbsent(root.right.val, k -> new ArrayList<>()).add(root.val);
        }
        dfs(root.left);
        dfs(root.right);
    }
}

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private Map<Integer, List<Integer>> g = new HashMap<>();

    public int amountOfTime(TreeNode root, int start) {
        dfs(root);
        return dfs(start, -1);
    }

    private int dfs(int i, int fa) {
        int ans = 0;
        for (int j : g.getOrDefault(i, Collections.emptyList())) {
            if (j != fa) {
                ans = Math.max(ans, 1 + dfs(j, i));
            }
        }
        return ans;
    }

    private void dfs(TreeNode root) {
        if (root == null) {
            return;
        }
        if (root.left != null) {
            g.computeIfAbsent(root.left.val, k -> new ArrayList<>()).add(root.val);
            g.computeIfAbsent(root.val, k -> new ArrayList<>()).add(root.left.val);
        }
        if (root.right != null) {
            g.computeIfAbsent(root.right.val, k -> new ArrayList<>()).add(root.val);
            g.computeIfAbsent(root.val, k -> new ArrayList<>()).add(root.right.val);
        }
        dfs(root.left);
        dfs(root.right);
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    unordered_map<int, vector<int>> g;

    int amountOfTime(TreeNode* root, int start) {
        dfs(root);
        queue<int> q{{start}};
        unordered_set<int> vis;
        int ans = -1;
        while (q.size()) {
            ++ans;
            for (int n = q.size(); n; --n) {
                int i = q.front();
                q.pop();
                vis.insert(i);
                for (int j : g[i]) {
                    if (!vis.count(j)) {
                        q.push(j);
                    }
                }
            }
        }
        return ans;
    }

    void dfs(TreeNode* root) {
        if (!root) return;
        if (root->left) {
            g[root->val].push_back(root->left->val);
            g[root->left->val].push_back(root->val);
        }
        if (root->right) {
            g[root->val].push_back(root->right->val);
            g[root->right->val].push_back(root->val);
        }
        dfs(root->left);
        dfs(root->right);
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    unordered_map<int, vector<int>> g;

    int amountOfTime(TreeNode* root, int start) {
        dfs(root);
        return dfs(start, -1);
    }

    int dfs(int i, int fa) {
        int ans = 0;
        for (int& j : g[i]) {
            if (j != fa) {
                ans = max(ans, 1 + dfs(j, i));
            }
        }
        return ans;
    }

    void dfs(TreeNode* root) {
        if (!root) return;
        if (root->left) {
            g[root->val].push_back(root->left->val);
            g[root->left->val].push_back(root->val);
        }
        if (root->right) {
            g[root->val].push_back(root->right->val);
            g[root->right->val].push_back(root->val);
        }
        dfs(root->left);
        dfs(root->right);
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func amountOfTime(root *TreeNode, start int) int {
	g := map[int][]int{}
	var dfs func(*TreeNode)
	dfs = func(root *TreeNode) {
		if root == nil {
			return
		}
		if root.Left != nil {
			g[root.Val] = append(g[root.Val], root.Left.Val)
			g[root.Left.Val] = append(g[root.Left.Val], root.Val)
		}
		if root.Right != nil {
			g[root.Val] = append(g[root.Val], root.Right.Val)
			g[root.Right.Val] = append(g[root.Right.Val], root.Val)
		}
		dfs(root.Left)
		dfs(root.Right)
	}

	dfs(root)
	q := []int{start}
	ans := -1
	vis := map[int]bool{}
	for len(q) > 0 {
		ans++
		for n := len(q); n > 0; n-- {
			i := q[0]
			q = q[1:]
			vis[i] = true
			for _, j := range g[i] {
				if !vis[j] {
					q = append(q, j)
				}
			}
		}
	}
	return ans
}

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func amountOfTime(root *TreeNode, start int) int {
	g := map[int][]int{}
	var dfs func(*TreeNode)
	dfs = func(root *TreeNode) {
		if root == nil {
			return
		}
		if root.Left != nil {
			g[root.Val] = append(g[root.Val], root.Left.Val)
			g[root.Left.Val] = append(g[root.Left.Val], root.Val)
		}
		if root.Right != nil {
			g[root.Val] = append(g[root.Val], root.Right.Val)
			g[root.Right.Val] = append(g[root.Right.Val], root.Val)
		}
		dfs(root.Left)
		dfs(root.Right)
	}

	var dfs2 func(int, int) int
	dfs2 = func(i, fa int) int {
		ans := 0
		for _, j := range g[i] {
			if j != fa {
				ans = max(ans, 1+dfs2(j, i))
			}
		}
		return ans
	}

	dfs(root)
	return dfs2(start, -1)
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

TypeScript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function amountOfTime(root: TreeNode | null, start: number): number {
    const map = new Map<number, number[]>();
    const create = ({ val, left, right }: TreeNode) => {
        if (left != null) {
            map.set(val, [...(map.get(val) ?? []), left.val]);
            map.set(left.val, [...(map.get(left.val) ?? []), val]);
            create(left);
        }
        if (right != null) {
            map.set(val, [...(map.get(val) ?? []), right.val]);
            map.set(right.val, [...(map.get(right.val) ?? []), val]);
            create(right);
        }
    };
    create(root);
    const dfs = (st: number, fa: number) => {
        let res = 0;
        for (const v of map.get(st) ?? []) {
            if (v !== fa) {
                res = Math.max(res, dfs(v, st) + 1);
            }
        }
        return res;
    };
    return dfs(start, -1);
}

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

2385.Amount of Time for Binary Tree to Be Infected

2385.Amount of Time for Binary Tree to Be Infected

README.md

2385. 感染二叉树需要的总时间

题目描述

解法

Python3

Java

C++

Go

TypeScript

...

Files

2385.Amount of Time for Binary Tree to Be Infected

Directory actions

More options

Directory actions

More options

Latest commit

History

2385.Amount of Time for Binary Tree to Be Infected

Folders and files

parent directory

README.md

2385. 感染二叉树需要的总时间

题目描述

解法

Python3

Java

C++

Go

TypeScript

...