3004. 相同颜色的最大子树

English Version

题目描述

给定一个二维整数数组 edges，表示一个有 n 个节点的树，节点编号从 0 到 n - 1，以节点 0 为根，其中 edges[i] = [ui, vi] 表示节点 vi 和 ui 之间存在一条边。

还给定一个 下标从 0 开始，大小为 n 的整数数组 colors，其中 colors[i] 表示节点 i 分配的颜色。

我们希望找到一个节点 v，使得 v 的子树中的每个节点具有 相同 的颜色。

返回 具有 尽可能多 节点 且 符合上述要求的子树大小。

 

示例 1：

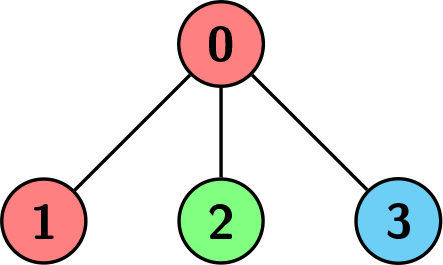
输入：edges = [[0,1],[0,2],[0,3]], colors = [1,1,2,3]
输出：1
解释：每种颜色分别对应为：1 -> 红色，2 -> 绿色，3 -> 蓝色。我们可以看到以节点 0 为根的子树具有不同颜色的子节点。任何其他子树都是相同颜色的，并且大小为 1。因此，我们返回 1。

示例 2：

输入：edges = [[0,1],[0,2],[0,3]], colors = [1,1,1,1]
输出：4
解释：整个树具有相同的颜色，以节点 0 为根的子树具有节点数最多，为 4。因此，我们返回 4。

示例 3：

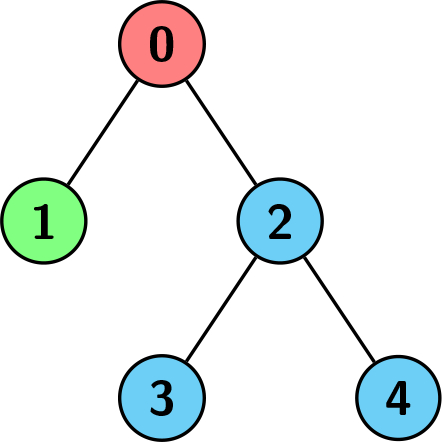
输入：edges = [[0,1],[0,2],[2,3],[2,4]], colors = [1,2,3,3,3]
输出：3
解释：每种颜色分别对应为：1 -> 红色，2 -> 绿色，3 -> 蓝色。我们可以看到以节点 0 为根的子树有不同颜色的子节点。其他任何子树都是相同颜色的，但以节点 2 为根的子树的大小为 3，这是最大的。因此，我们返回 3。

 

提示：

• n == edges.length + 1
• 1 <= n <= 5 * 104
• edges[i] == [ui, vi]
• 0 <= ui, vi < n
• colors.length == n
• 1 <= colors[i] <= 105
• 输入被生成，使得由 edges 表示的图是一棵树。

解法

方法一：DFS

我们先根据题目给定的边的信息，构建一个邻接表 $g$，其中 $g[a]$ 表示节点 $a$ 的所有相邻节点。然后我们创建一个长度为 $n$ 的数组 $size$，其中 $size[a]$ 表示以节点 $a$ 为根的子树的节点数。

接下来，我们设计一个函数 $dfs(a, fa)$，它将返回以节点 $a$ 为根的子树是否满足题目要求。函数 $dfs(a, fa)$ 的执行过程如下：

• 首先，我们用一个变量 $ok$ 记录以节点 $a$ 为根的子树是否满足题目要求，初始时 $ok$ 为 $true$。
• 接着，我们遍历节点 $a$ 的所有相邻节点 $b$，如果 $b$ 不是 $a$ 的父节点 $fa$，那么我们递归调用 $dfs(b, a)$，并将返回值保存到变量 $t$ 中，并且更新 $ok$ 为 $ok$ 与 $colors[a] = colors[b] \land t$ 的值，其中 $\land$ 表示逻辑与运算。然后，我们更新 $size[a] = size[a] + size[b]$。
• 然后，我们判断 $ok$ 的值，如果 $ok$ 为 $true$，那么我们更新答案 $ans = \max(ans, size[a])$。
• 最后，我们返回 $ok$ 的值。

我们调用 $dfs(0, -1)$，其中 $0$ 表示根节点的编号，$-1$ 表示根节点没有父节点。最终的答案即为 $ans$。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是节点的数量。

class Solution:
    def maximumSubtreeSize(self, edges: List[List[int]], colors: List[int]) -> int:
        def dfs(a: int, fa: int) -> bool:
            ok = True
            for b in g[a]:
                if b != fa:
                    t = dfs(b, a)
                    ok = ok and colors[a] == colors[b] and t
                    size[a] += size[b]
            if ok:
                nonlocal ans
                ans = max(ans, size[a])
            return ok

        n = len(edges) + 1
        g = [[] for _ in range(n)]
        size = [1] * n
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        ans = 0
        dfs(0, -1)
        return ans

class Solution {
    private List<Integer>[] g;
    private int[] colors;
    private int[] size;
    private int ans;

    public int maximumSubtreeSize(int[][] edges, int[] colors) {
        int n = edges.length + 1;
        g = new List[n];
        size = new int[n];
        this.colors = colors;
        Arrays.fill(size, 1);
        Arrays.setAll(g, i -> new ArrayList<>());
        for (var e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        dfs(0, -1);
        return ans;
    }

    private boolean dfs(int a, int fa) {
        boolean ok = true;
        for (int b : g[a]) {
            if (b != fa) {
                boolean t = dfs(b, a);
                ok = ok && colors[a] == colors[b] && t;
                size[a] += size[b];
            }
        }
        if (ok) {
            ans = Math.max(ans, size[a]);
        }
        return ok;
    }
}

class Solution {
public:
    int maximumSubtreeSize(vector<vector<int>>& edges, vector<int>& colors) {
        int n = edges.size() + 1;
        vector<int> g[n];
        vector<int> size(n, 1);
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }
        int ans = 0;
        function<bool(int, int)> dfs = [&](int a, int fa) {
            bool ok = true;
            for (int b : g[a]) {
                if (b != fa) {
                    bool t = dfs(b, a);
                    ok = ok && colors[a] == colors[b] && t;
                    size[a] += size[b];
                }
            }
            if (ok) {
                ans = max(ans, size[a]);
            }
            return ok;
        };
        dfs(0, -1);
        return ans;
    }
};

func maximumSubtreeSize(edges [][]int, colors []int) (ans int) {
	n := len(edges) + 1
	g := make([][]int, n)
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	size := make([]int, n)
	var dfs func(int, int) bool
	dfs = func(a, fa int) bool {
		size[a] = 1
		ok := true
		for _, b := range g[a] {
			if b != fa {
				t := dfs(b, a)
				ok = ok && t && colors[a] == colors[b]
				size[a] += size[b]
			}
		}
		if ok {
			ans = max(ans, size[a])
		}
		return ok
	}
	dfs(0, -1)
	return
}

function maximumSubtreeSize(edges: number[][], colors: number[]): number {
    const n = edges.length + 1;
    const g: number[][] = Array.from({ length: n }, () => []);
    for (const [a, b] of edges) {
        g[a].push(b);
        g[b].push(a);
    }
    const size: number[] = Array(n).fill(1);
    let ans = 0;
    const dfs = (a: number, fa: number): boolean => {
        let ok = true;
        for (const b of g[a]) {
            if (b !== fa) {
                const t = dfs(b, a);
                ok = ok && t && colors[a] === colors[b];
                size[a] += size[b];
            }
        }
        if (ok) {
            ans = Math.max(ans, size[a]);
        }
        return ok;
    };
    dfs(0, -1);
    return ans;
}