给定二叉树的根 root,具有以下属性:
- 叶节点 的值为
0或1,分别表示false和true。 - 非叶节点的值为
2、3、4、5,分别表示布尔运算OR,AND,XOR,NOT。
您还将得到一个布尔型 result,这是 root 节点的期望 评价 结果。
对节点的评价计算如下:
- 如果节点是叶节点,则评价是节点的 值,即
true或false. - 否则, 将其值的布尔运算应用于子节点的 评价,该节点的 评价 即为布尔运算后的结果。
在一个操作中,您可以 翻转 一个叶节点,这将导致一个 false 节点变为 true 节点,一个 true 节点变为 false 节点。
返回需要执行的最小操作数,以使 root 的评价得到 result。可以证明,总有办法达到 result。
叶节点 是没有子节点的节点。
注意: NOT 节点只有左孩子或只有右孩子,但其他非叶节点同时拥有左孩子和右孩子。
示例 1:
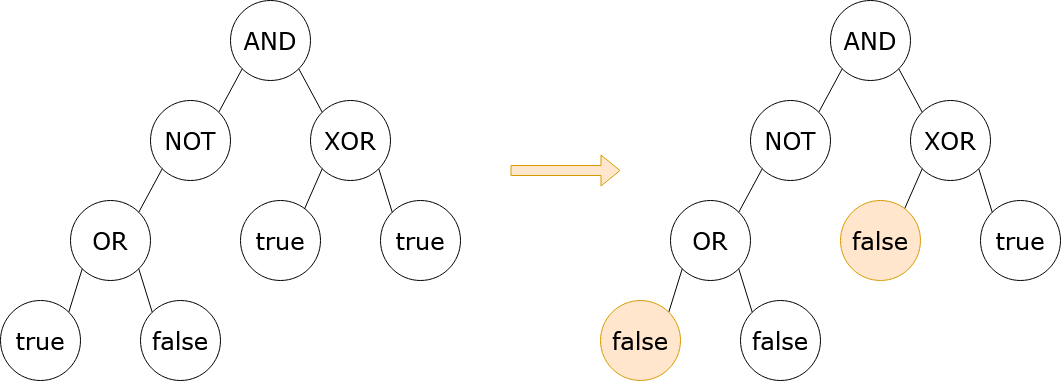
输入: root = [3,5,4,2,null,1,1,1,0], result = true 输出: 2 解释: 可以证明,至少需要翻转 2 个节点才能使树的 root 评价为 true。上面的图显示了实现这一目标的一种方法。
示例 2:
输入: root = [0], result = false 输出: 0 解释: 树的 root 的评价已经为 false,所以 0 个节点必须翻转。
提示:
- 树中的节点数在
[1, 105]范围内。 0 <= Node.val <= 5OR,AND,XOR节点有2个子节点。NOT只有一个1子节点。- 叶节点的值为
0或1. - 非叶节点的值为
2,3,4,5.
我们定义一个函数 false 所需要的最少翻转次数,第二个表示将 true 所需要的最少翻转次数。那么答案为
函数
如果
否则,我们记
- 如果
$x \in {0, 1}$ ,那么返回$[x, x \oplus 1]$ 。 - 如果
$x = 2$ ,即布尔运算符是OR,为了使$root$ 的值为false,我们需要将左右子树的值都变成false,因此返回值的第一个元素为$l[0] + r[0]$ ;为了使$root$ 的值为true,我们需要将左右子树的值中至少有一个变成true,因此返回值的第二个元素为$\min(l[0] + r[1], l[1] + r[0], l[1] + r[1])$ 。 - 如果
$x = 3$ ,即布尔运算符是AND,为了使$root$ 的值为false,我们需要将左右子树的值中至少有一个变成false,因此返回值的第一个元素为$\min(l[0] + r[0], l[0] + r[1], l[1] + r[0])$ ;为了使$root$ 的值为true,我们需要将左右子树的值都变成true,因此返回值的第二个元素为$l[1] + r[1]$ 。 - 如果
$x = 4$ ,即布尔运算符是XOR,为了使$root$ 的值为false,我们需要将左右子树的值同为false或同为true,因此返回值的第一个元素为$\min(l[0] + r[0], l[1] + r[1])$ ;为了使$root$ 的值为true,我们需要将左右子树的值不同,因此返回值的第二个元素为$\min(l[0] + r[1], l[1] + r[0])$ 。 - 如果
$x = 5$ ,即布尔运算符是NOT,为了使$root$ 的值为false,我们需要将左右子树的值中至少有一个变成true,因此返回值的第一个元素为$\min(l[1], r[1])$ ;为了使$root$ 的值为true,我们需要将左右子树的值中至少有一个变成false,因此返回值的第二个元素为$\min(l[0], r[0])$ 。
时间复杂度
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minimumFlips(self, root: Optional[TreeNode], result: bool) -> int:
def dfs(root: Optional[TreeNode]) -> (int, int):
if root is None:
return inf, inf
x = root.val
if x in (0, 1):
return x, x ^ 1
l, r = dfs(root.left), dfs(root.right)
if x == 2:
return l[0] + r[0], min(l[0] + r[1], l[1] + r[0], l[1] + r[1])
if x == 3:
return min(l[0] + r[0], l[0] + r[1], l[1] + r[0]), l[1] + r[1]
if x == 4:
return min(l[0] + r[0], l[1] + r[1]), min(l[0] + r[1], l[1] + r[0])
return min(l[1], r[1]), min(l[0], r[0])
return dfs(root)[int(result)]/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int minimumFlips(TreeNode root, boolean result) {
return dfs(root)[result ? 1 : 0];
}
private int[] dfs(TreeNode root) {
if (root == null) {
return new int[] {1 << 30, 1 << 30};
}
int x = root.val;
if (x < 2) {
return new int[] {x, x ^ 1};
}
var l = dfs(root.left);
var r = dfs(root.right);
int a = 0, b = 0;
if (x == 2) {
a = l[0] + r[0];
b = Math.min(l[0] + r[1], Math.min(l[1] + r[0], l[1] + r[1]));
} else if (x == 3) {
a = Math.min(l[0] + r[0], Math.min(l[0] + r[1], l[1] + r[0]));
b = l[1] + r[1];
} else if (x == 4) {
a = Math.min(l[0] + r[0], l[1] + r[1]);
b = Math.min(l[0] + r[1], l[1] + r[0]);
} else {
a = Math.min(l[1], r[1]);
b = Math.min(l[0], r[0]);
}
return new int[] {a, b};
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int minimumFlips(TreeNode* root, bool result) {
function<pair<int, int>(TreeNode*)> dfs = [&](TreeNode* root) -> pair<int, int> {
if (!root) {
return {1 << 30, 1 << 30};
}
int x = root->val;
if (x < 2) {
return {x, x ^ 1};
}
auto [l0, l1] = dfs(root->left);
auto [r0, r1] = dfs(root->right);
int a = 0, b = 0;
if (x == 2) {
a = l0 + r0;
b = min({l0 + r1, l1 + r0, l1 + r1});
} else if (x == 3) {
a = min({l0 + r0, l0 + r1, l1 + r0});
b = l1 + r1;
} else if (x == 4) {
a = min(l0 + r0, l1 + r1);
b = min(l0 + r1, l1 + r0);
} else {
a = min(l1, r1);
b = min(l0, r0);
}
return {a, b};
};
auto [a, b] = dfs(root);
return result ? b : a;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func minimumFlips(root *TreeNode, result bool) int {
var dfs func(*TreeNode) (int, int)
dfs = func(root *TreeNode) (int, int) {
if root == nil {
return 1 << 30, 1 << 30
}
x := root.Val
if x < 2 {
return x, x ^ 1
}
l0, l1 := dfs(root.Left)
r0, r1 := dfs(root.Right)
var a, b int
if x == 2 {
a = l0 + r0
b = min(l0+r1, min(l1+r0, l1+r1))
} else if x == 3 {
a = min(l0+r0, min(l0+r1, l1+r0))
b = l1 + r1
} else if x == 4 {
a = min(l0+r0, l1+r1)
b = min(l0+r1, l1+r0)
} else {
a = min(l1, r1)
b = min(l0, r0)
}
return a, b
}
a, b := dfs(root)
if result {
return b
}
return a
}/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function minimumFlips(root: TreeNode | null, result: boolean): number {
const dfs = (root: TreeNode | null): [number, number] => {
if (!root) {
return [1 << 30, 1 << 30];
}
const x = root.val;
if (x < 2) {
return [x, x ^ 1];
}
const [l0, l1] = dfs(root.left);
const [r0, r1] = dfs(root.right);
if (x === 2) {
return [l0 + r0, Math.min(l0 + r1, l1 + r0, l1 + r1)];
}
if (x === 3) {
return [Math.min(l0 + r0, l0 + r1, l1 + r0), l1 + r1];
}
if (x === 4) {
return [Math.min(l0 + r0, l1 + r1), Math.min(l0 + r1, l1 + r0)];
}
return [Math.min(l1, r1), Math.min(l0, r0)];
};
return dfs(root)[result ? 1 : 0];
}