Skip to content

Latest commit

 

History

History

1612.Check If Two Expression Trees are Equivalent

Folders and files

NameName
Last commit message
Last commit date

parent directory

..
images
images
 
 
README.md
README.md
 
 
README_EN.md
README_EN.md
 
 
Solution.cpp
Solution.cpp
 
 
Solution.java
Solution.java
 
 
Solution.js
Solution.js
 
 
Solution.py
Solution.py
 
 

README.md

1612. 检查两棵二叉表达式树是否等价

English Version

题目描述

二叉表达式树是一种表达算术表达式的二叉树。二叉表达式树中的每一个节点都有零个或两个子节点。 叶节点（有 0 个子节点的节点）表示操作数，非叶节点（有 2 个子节点的节点）表示运算符。在本题中，我们只考虑 '+' 运算符（即加法）。

给定两棵二叉表达式树的根节点 root1 和 root2 。如果两棵二叉表达式树等价，返回 true ，否则返回 false 。

当两棵二叉搜索树中的变量取任意值，分别求得的值都相等时，我们称这两棵二叉表达式树是等价的。

 

示例 1:

输入： root1 = [x], root2 = [x]
输出： true

示例 2:

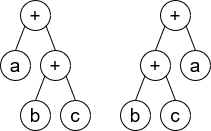
输入：root1 = [+,a,+,null,null,b,c], root2 = [+,+,a,b,c]
输出：true
解释：a + (b + c) == (b + c) + a

示例 3:

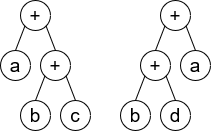
输入： root1 = [+,a,+,null,null,b,c], root2 = [+,+,a,b,d]
输出： false
解释： a + (b + c) != (b + d) + a

 

提示：

  • 两棵树中的节点个数相等，且节点个数为范围 [1, 4999] 内的奇数。
  • Node.val 是 '+' 或小写英文字母。
  • 给定的树保证是有效的二叉表达式树。

 

进阶：当你的答案需同时支持 '-' 运算符（减法）时，你该如何修改你的答案

解法

方法一：递归

我们定义一个计数器 $cnt$，用于统计每个字母出现的次数。

然后我们分别对两棵二叉表达式树进行深度优先搜索，如果字母出现在左子树，则 $cnt$ 中对应的字母的值加 $1$，如果出现在右子树，则 $cnt$ 中对应的字母的值减 $1$。

最后，我们遍历 $cnt$，如果所有字母的值都为 $0$，则返回 true，否则返回 false。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是二叉表达式树的节点个数。

Python3

# Definition for a binary tree node.
# class Node(object):
#     def __init__(self, val=" ", left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def checkEquivalence(self, root1: 'Node', root2: 'Node') -> bool:
        def dfs(root, v):
            if root is None:
                return
            if root.val != '+':
                cnt[root.val] += v
            dfs(root.left, v)
            dfs(root.right, v)

        cnt = Counter()
        dfs(root1, 1)
        dfs(root2, -1)
        return all(x == 0 for x in cnt.values())
# Definition for a binary tree node.
# class Node(object):
#     def __init__(self, val=" ", left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def checkEquivalence(self, root1: 'Node', root2: 'Node') -> bool:
        def dfs(root):
            cnt = [0] * 26
            if root is None:
                return cnt
            if root.val in '+-':
                l, r = dfs(root.left), dfs(root.right)
                k = 1 if root.val == '+' else -1
                for i in range(26):
                    cnt[i] += l[i] + r[i] * k
            else:
                cnt[ord(root.val) - ord('a')] += 1
            return cnt

        return dfs(root1) == dfs(root2)

Java

/**
 * Definition for a binary tree node.
 * class Node {
 *     char val;
 *     Node left;
 *     Node right;
 *     Node() {this.val = ' ';}
 *     Node(char val) { this.val = val; }
 *     Node(char val, Node left, Node right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int[] cnt = new int[26];

    public boolean checkEquivalence(Node root1, Node root2) {
        dfs(root1, 1);
        dfs(root2, -1);
        for (int x : cnt) {
            if (x != 0) {
                return false;
            }
        }
        return true;
    }

    private void dfs(Node root, int v) {
        if (root == null) {
            return;
        }
        if (root.val != '+') {
            cnt[root.val - 'a'] += v;
        }
        dfs(root.left, v);
        dfs(root.right, v);
    }
}
/**
 * Definition for a binary tree node.
 * class Node {
 *     char val;
 *     Node left;
 *     Node right;
 *     Node() {this.val = ' ';}
 *     Node(char val) { this.val = val; }
 *     Node(char val, Node left, Node right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean checkEquivalence(Node root1, Node root2) {
        int[] cnt1 = dfs(root1);
        int[] cnt2 = dfs(root2);
        for (int i = 0; i < 26; ++i) {
            if (cnt1[i] != cnt2[i]) {
                return false;
            }
        }
        return true;
    }

    private int[] dfs(Node root) {
        int[] cnt = new int[26];
        if (root == null) {
            return cnt;
        }
        if (root.val == '+' || root.val == '-') {
            int[] l = dfs(root.left);
            int[] r = dfs(root.right);
            int k = root.val == '+' ? 1 : -1;
            for (int i = 0; i < 26; ++i) {
                cnt[i] += l[i] + r[i] * k;
            }
        } else {
            cnt[root.val - 'a']++;
        }
        return cnt;
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct Node {
 *     char val;
 *     Node *left;
 *     Node *right;
 *     Node() : val(' '), left(nullptr), right(nullptr) {}
 *     Node(char x) : val(x), left(nullptr), right(nullptr) {}
 *     Node(char x, Node *left, Node *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool checkEquivalence(Node* root1, Node* root2) {
        int cnt[26]{};
        function<void(Node*, int)> dfs = [&](Node* root, int v) {
            if (!root) {
                return;
            }
            if (root->val != '+') {
                cnt[root->val - 'a'] += v;
            }
            dfs(root->left, v);
            dfs(root->right, v);
        };
        dfs(root1, 1);
        dfs(root2, -1);
        for (int& x : cnt) {
            if (x) {
                return false;
            }
        }
        return true;
    }
};
/**
 * Definition for a binary tree node.
 * struct Node {
 *     char val;
 *     Node *left;
 *     Node *right;
 *     Node() : val(' '), left(nullptr), right(nullptr) {}
 *     Node(char x) : val(x), left(nullptr), right(nullptr) {}
 *     Node(char x, Node *left, Node *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool checkEquivalence(Node* root1, Node* root2) {
        function<vector<int>(Node*)> dfs = [&](Node* root) -> vector<int> {
            vector<int> cnt(26);
            if (!root) {
                return cnt;
            }
            if (root->val == '+' || root->val == '-') {
                auto l = dfs(root->left);
                auto r = dfs(root->right);
                int k = root->val == '+' ? 1 : -1;
                for (int i = 0; i < 26; ++i) {
                    cnt[i] += l[i] + r[i] * k;
                }
            } else {
                cnt[root->val - 'a']++;
            }
            return cnt;
        };
        return dfs(root1) == dfs(root2);
    }
};

JavaScript

/**
 * Definition for a binary tree node.
 * function Node(val, left, right) {
 *     this.val = (val===undefined ? " " : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {Node} root1
 * @param {Node} root2
 * @return {boolean}
 */
var checkEquivalence = function (root1, root2) {
    const cnt = new Array(26).fill(0);
    const dfs = (root, v) => {
        if (!root) {
            return;
        }
        if (root.val !== '+') {
            cnt[root.val.charCodeAt(0) - 'a'.charCodeAt(0)] += v;
        }
        dfs(root.left, v);
        dfs(root.right, v);
    };
    dfs(root1, 1);
    dfs(root2, -1);
    for (const x of cnt) {
        if (x) {
            return false;
        }
    }
    return true;
};
/**
 * Definition for a binary tree node.
 * function Node(val, left, right) {
 *     this.val = (val===undefined ? " " : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {Node} root1
 * @param {Node} root2
 * @return {boolean}
 */
var checkEquivalence = function (root1, root2) {
    const dfs = root => {
        const cnt = new Array(26).fill(0);
        if (!root) {
            return cnt;
        }
        if (root.val === '+' || root.val === '-') {
            const l = dfs(root.left);
            const r = dfs(root.right);
            const k = root.val === '+' ? 1 : -1;
            for (let i = 0; i < 26; ++i) {
                cnt[i] = l[i] + k * r[i];
            }
        } else {
            cnt[root.val.charCodeAt(0) - 'a'.charCodeAt(0)]++;
        }
        return cnt;
    };
    const cnt1 = dfs(root1);
    const cnt2 = dfs(root2);
    for (let i = 0; i < 26; ++i) {
        if (cnt1[i] !== cnt2[i]) {
            return false;
        }
    }
    return true;
};

...