diff --git "a/lcof2/\345\211\221\346\214\207 Offer II 058. \346\227\245\347\250\213\350\241\250/README.md" "b/lcof2/\345\211\221\346\214\207 Offer II 058. \346\227\245\347\250\213\350\241\250/README.md"
index 0533deb7d3140..a3933de14e03c 100644
--- "a/lcof2/\345\211\221\346\214\207 Offer II 058. \346\227\245\347\250\213\350\241\250/README.md"
+++ "b/lcof2/\345\211\221\346\214\207 Offer II 058. \346\227\245\347\250\213\350\241\250/README.md"
@@ -164,11 +164,11 @@ class MyCalendar {
func book(_ start: Int, _ end: Int) -> Bool {
let newEvent = (start, end)
let index = calendar.firstIndex { $0.0 >= newEvent.1 } ?? calendar.count
-
+
if index > 0 && calendar[index - 1].1 > newEvent.0 {
return false
}
-
+
calendar.insert(newEvent, at: index)
return true
}
diff --git a/solution/0500-0599/0523.Continuous Subarray Sum/README.md b/solution/0500-0599/0523.Continuous Subarray Sum/README.md
index 2c49787a853c0..f93e7538db272 100644
--- a/solution/0500-0599/0523.Continuous Subarray Sum/README.md
+++ b/solution/0500-0599/0523.Continuous Subarray Sum/README.md
@@ -19,18 +19,23 @@ tags:
-给你一个整数数组 nums 和一个整数 k ,编写一个函数来判断该数组是否含有同时满足下述条件的连续子数组:
+给你一个整数数组 nums 和一个整数 k ,如果 nums 有一个 好的子数组 返回 true ,否则返回 false:
+
+一个 好的子数组 是:
- - 子数组大小 至少为 2 ,且
+ - 长度 至少为 2 ,且
- 子数组元素总和为
k 的倍数。
-如果存在,返回 true ;否则,返回 false 。
+注意:
-如果存在一个整数 n ,令整数 x 符合 x = n * k ,则称 x 是 k 的一个倍数。0 始终视为 k 的一个倍数。
+
+ - 子数组 是数组中 连续 的部分。
+ - 如果存在一个整数
n ,令整数 x 符合 x = n * k ,则称 x 是 k 的一个倍数。0 始终 视为 k 的一个倍数。
+
-
+
示例 1:
@@ -55,15 +60,15 @@ tags:
输出:false
-
+
提示:
- 1 <= nums.length <= 1050 <= nums[i] <= 1090 <= sum(nums[i]) <= 231 - 11 <= k <= 231 - 11 <= nums.length <= 1050 <= nums[i] <= 1090 <= sum(nums[i]) <= 231 - 11 <= k <= 231 - 1
diff --git a/solution/0900-0999/0974.Subarray Sums Divisible by K/README.md b/solution/0900-0999/0974.Subarray Sums Divisible by K/README.md
index 96ffad06b9d64..236956ae39cb5 100644
--- a/solution/0900-0999/0974.Subarray Sums Divisible by K/README.md
+++ b/solution/0900-0999/0974.Subarray Sums Divisible by K/README.md
@@ -18,9 +18,9 @@ tags:
-给定一个整数数组 nums 和一个整数 k ,返回其中元素之和可被 k 整除的(连续、非空) 子数组 的数目。
+给定一个整数数组 nums 和一个整数 k ,返回其中元素之和可被 k 整除的非空 子数组 的数目。
-子数组 是数组的 连续 部分。
+子数组 是数组中 连续 的部分。
diff --git a/solution/1000-1099/1090.Largest Values From Labels/README.md b/solution/1000-1099/1090.Largest Values From Labels/README.md
index 7814a000020f3..7b2ca61e0f94a 100644
--- a/solution/1000-1099/1090.Largest Values From Labels/README.md
+++ b/solution/1000-1099/1090.Largest Values From Labels/README.md
@@ -22,44 +22,54 @@ tags:
-我们有一个 n 项的集合。给出两个整数数组 values 和 labels ,第 i 个元素的值和标签分别是 values[i] 和 labels[i]。还会给出两个整数 numWanted 和 useLimit 。
+以两个整数数组 values 和 labels 给定 n 个项的值和标签,并且给出两个整数 numWanted 和 useLimit 。
-从 n 个元素中选择一个子集 s :
+你的任务是从这些项中找到一个值的和 最大 的子集使得:
- - 子集
s 的大小 小于或等于 numWanted 。
- s 中 最多 有相同标签的 useLimit 项。- 项的数量 最多 为
numWanted。
+ - 相同标签的项的数量 最多 为
useLimit。
-一个子集的 分数 是该子集的值之和。
-
-返回子集 s 的最大 分数 。
+返回最大的和。
-示例 1:
+示例 1:
+
+
+
输入:values = [5,4,3,2,1], labels = [1,1,2,2,3], numWanted = 3, useLimit = 1
+
+
输出:9
+
+
解释:
+
+
选择的子集是第一个、第三个和第五个项,其值之和为 5 + 3 + 1。
+
示例 2:
+
+
+
输入:values = [5,4,3,2,1], labels = [1,3,3,3,2], numWanted = 3, useLimit = 2
+
+
输出:12
+
+
解释:
+
+
选择的子集是第一个、第二个和第三个项,其值之和为 5 + 4 + 3。
+
-输入:values = [5,4,3,2,1], labels = [1,1,2,2,3], numWanted = 3, useLimit = 1
-输出:9
-解释:选出的子集是第一项,第三项和第五项。
-
+示例 3:
-示例 2:
+
+
输入:values = [9,8,8,7,6], labels = [0,0,0,1,1], numWanted = 3, useLimit = 1
-
-输入:values = [5,4,3,2,1], labels = [1,3,3,3,2], numWanted = 3, useLimit = 2
-输出:12
-解释:选出的子集是第一项,第二项和第三项。
-
+
输出:16
-
示例 3:
+
解释:
-
-输入:values = [9,8,8,7,6], labels = [0,0,0,1,1], numWanted = 3, useLimit = 1
-输出:16
-解释:选出的子集是第一项和第四项。
-
+
选择的子集是第一个和第四个项,其值之和为 9 + 7。
+
diff --git a/solution/1200-1299/1240.Tiling a Rectangle with the Fewest Squares/README.md b/solution/1200-1299/1240.Tiling a Rectangle with the Fewest Squares/README.md
index f78be7f78e372..86d73e72495d8 100644
--- a/solution/1200-1299/1240.Tiling a Rectangle with the Fewest Squares/README.md
+++ b/solution/1200-1299/1240.Tiling a Rectangle with the Fewest Squares/README.md
@@ -30,9 +30,10 @@ tags:
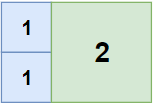
示例 1:
-
+
-输入:n = 2, m = 3
+
+输入:n = 2, m = 3
输出:3
解释:3 块地砖就可以铺满卧室。
2 块 1x1 地砖
@@ -40,17 +41,19 @@ tags:
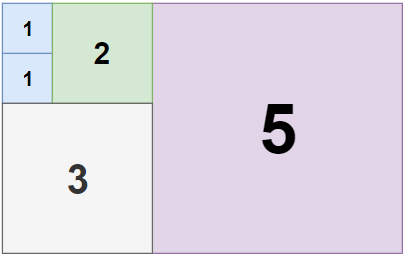
示例 2:
-
+
-输入:n = 5, m = 8
+
+输入:n = 5, m = 8
输出:5
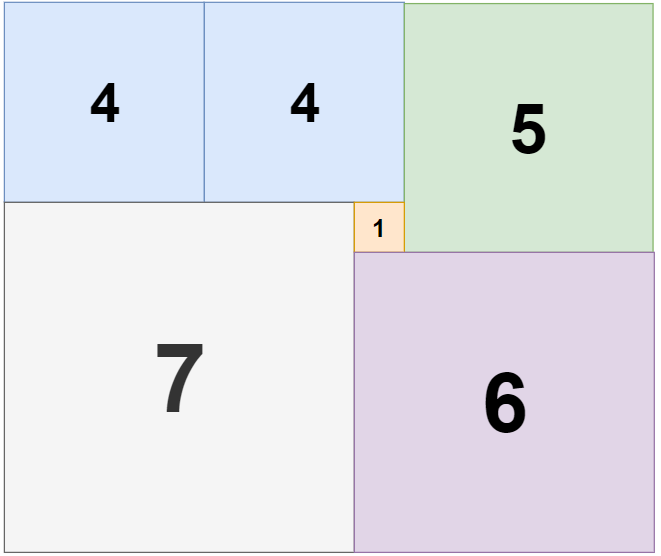
示例 3:
-
+
-输入:n = 11, m = 13
+
+输入:n = 11, m = 13
输出:6
@@ -59,8 +62,7 @@ tags:
提示:
- 1 <= n <= 131 <= m <= 131 <= n, m <= 13
diff --git a/solution/1500-1599/1597.Build Binary Expression Tree From Infix Expression/README.md b/solution/1500-1599/1597.Build Binary Expression Tree From Infix Expression/README.md
index 8c754f389706e..526926b2d1d6e 100644
--- a/solution/1500-1599/1597.Build Binary Expression Tree From Infix Expression/README.md
+++ b/solution/1500-1599/1597.Build Binary Expression Tree From Infix Expression/README.md
@@ -66,7 +66,7 @@ tags:
1 <= s.length <= 100s 中包含数字和字符 '+'、 '-'、 '*'、 '/' 。s 中包含数字和字符 '('、 ')'、'+'、 '-'、 '*'、 '/' 。s 中的操作数 恰好 是一位数字。- 题目数据保证
s 是一个有效的表达式。
diff --git a/solution/1500-1599/1597.Build Binary Expression Tree From Infix Expression/README_EN.md b/solution/1500-1599/1597.Build Binary Expression Tree From Infix Expression/README_EN.md
index c07b03e29010e..8b33f9dd869b2 100644
--- a/solution/1500-1599/1597.Build Binary Expression Tree From Infix Expression/README_EN.md
+++ b/solution/1500-1599/1597.Build Binary Expression Tree From Infix Expression/README_EN.md
@@ -65,7 +65,7 @@ The third tree below is also not valid. Although it produces the same result and
1 <= s.length <= 100s consists of digits and the characters '+', '-', '*', and '/'.s consists of digits and the characters '(', ')', '+', '-', '*', and '/'.- Operands in
s are exactly 1 digit.
- It is guaranteed that
s is a valid expression.
diff --git a/solution/2700-2799/2779.Maximum Beauty of an Array After Applying Operation/README.md b/solution/2700-2799/2779.Maximum Beauty of an Array After Applying Operation/README.md
index a80b6b04e3a96..2e76c67128708 100644
--- a/solution/2700-2799/2779.Maximum Beauty of an Array After Applying Operation/README.md
+++ b/solution/2700-2799/2779.Maximum Beauty of an Array After Applying Operation/README.md
@@ -80,11 +80,11 @@ tags:
我们注意到,对于每一次操作,区间 $[nums[i]-k, nums[i]+k]$ 内的所有元素都会增加 $1$,因此我们可以使用差分数组来记录这些操作对美丽值的贡献。
-题目中 $nums[i]-k$ 可能为负数,我们统一将所有元素加上 $k$,保证结果为非负数。因此,我们需要创建一个长度为 $\max(nums) + k \times 2 + 2$ 的差分数组 $d$。
+题目中 $nums[i]-k$ 可能为负数,我们统一将所有元素加上 $k$,保证结果为非负数。因此,我们可以创建一个长度为 $\max(nums) + k \times 2 + 2$ 的差分数组 $d$。
接下来,遍历数组 $nums$,对于当前遍历到的元素 $x$,我们将 $d[x]$ 增加 $1$,将 $d[x+k\times2+1]$ 减少 $1$。这样,我们就可以通过 $d$ 数组计算出每个位置的前缀和,即为每个位置的美丽值。找到最大的美丽值即可。
-时间复杂度 $O(n)$,空间复杂度 $O(M + 2 \times k)$。其中 $n$ 是数组 $nums$ 的长度,而 $M$ 是数组 $nums$ 中的最大值。
+时间复杂度 $O(M + 2 \times k + n)$,空间复杂度 $O(M + 2 \times k)$。其中 $n$ 是数组 $nums$ 的长度,而 $M$ 是数组 $nums$ 中的最大值。
@@ -98,11 +98,7 @@ class Solution:
for x in nums:
d[x] += 1
d[x + k * 2 + 1] -= 1
- ans = s = 0
- for x in d:
- s += x
- ans = max(ans, s)
- return ans
+ return max(accumulate(d))
```
#### Java
@@ -175,7 +171,7 @@ func maximumBeauty(nums []int, k int) (ans int) {
```ts
function maximumBeauty(nums: number[], k: number): number {
const m = Math.max(...nums) + k * 2 + 2;
- const d: number[] = new Array(m).fill(0);
+ const d: number[] = Array(m).fill(0);
for (const x of nums) {
d[x]++;
d[x + k * 2 + 1]--;
diff --git a/solution/2700-2799/2779.Maximum Beauty of an Array After Applying Operation/README_EN.md b/solution/2700-2799/2779.Maximum Beauty of an Array After Applying Operation/README_EN.md
index c7fa96f1804de..96f2e278ecc77 100644
--- a/solution/2700-2799/2779.Maximum Beauty of an Array After Applying Operation/README_EN.md
+++ b/solution/2700-2799/2779.Maximum Beauty of an Array After Applying Operation/README_EN.md
@@ -74,7 +74,15 @@ The beauty of the array nums is 4 (whole array).
-### Solution 1
+### Solution 1: Difference Array
+
+We notice that for each operation, all elements within the interval $[nums[i]-k, nums[i]+k]$ will increase by $1$. Therefore, we can use a difference array to record the contributions of these operations to the beauty value.
+
+In the problem, $nums[i]-k$ might be negative. We add $k$ to all elements to ensure the results are non-negative. Thus, we can create a difference array $d$ with a length of $\max(nums) + k \times 2 + 2$.
+
+Next, we iterate through the array $nums$. For the current element $x$ being iterated, we increase $d[x]$ by $1$ and decrease $d[x+k\times2+1]$ by $1$. In this way, we can calculate the prefix sum for each position using the $d$ array, which represents the beauty value for each position. The maximum beauty value can then be found.
+
+The time complexity is $O(M + 2 \times k + n)$, and the space complexity is $O(M + 2 \times k)$. Here, $n$ is the length of the array $nums$, and $M$ is the maximum value in the array $nums$.
@@ -88,11 +96,7 @@ class Solution:
for x in nums:
d[x] += 1
d[x + k * 2 + 1] -= 1
- ans = s = 0
- for x in d:
- s += x
- ans = max(ans, s)
- return ans
+ return max(accumulate(d))
```
#### Java
@@ -165,7 +169,7 @@ func maximumBeauty(nums []int, k int) (ans int) {
```ts
function maximumBeauty(nums: number[], k: number): number {
const m = Math.max(...nums) + k * 2 + 2;
- const d: number[] = new Array(m).fill(0);
+ const d: number[] = Array(m).fill(0);
for (const x of nums) {
d[x]++;
d[x + k * 2 + 1]--;
diff --git a/solution/2700-2799/2779.Maximum Beauty of an Array After Applying Operation/Solution.py b/solution/2700-2799/2779.Maximum Beauty of an Array After Applying Operation/Solution.py
index b8fdf62a505ee..0f11f15efe89a 100644
--- a/solution/2700-2799/2779.Maximum Beauty of an Array After Applying Operation/Solution.py
+++ b/solution/2700-2799/2779.Maximum Beauty of an Array After Applying Operation/Solution.py
@@ -5,8 +5,4 @@ def maximumBeauty(self, nums: List[int], k: int) -> int:
for x in nums:
d[x] += 1
d[x + k * 2 + 1] -= 1
- ans = s = 0
- for x in d:
- s += x
- ans = max(ans, s)
- return ans
+ return max(accumulate(d))
diff --git a/solution/2700-2799/2779.Maximum Beauty of an Array After Applying Operation/Solution.ts b/solution/2700-2799/2779.Maximum Beauty of an Array After Applying Operation/Solution.ts
index 54bd5c64da227..37a8b53c986b3 100644
--- a/solution/2700-2799/2779.Maximum Beauty of an Array After Applying Operation/Solution.ts
+++ b/solution/2700-2799/2779.Maximum Beauty of an Array After Applying Operation/Solution.ts
@@ -1,6 +1,6 @@
function maximumBeauty(nums: number[], k: number): number {
const m = Math.max(...nums) + k * 2 + 2;
- const d: number[] = new Array(m).fill(0);
+ const d: number[] = Array(m).fill(0);
for (const x of nums) {
d[x]++;
d[x + k * 2 + 1]--;
diff --git a/solution/2800-2899/2862.Maximum Element-Sum of a Complete Subset of Indices/README.md b/solution/2800-2899/2862.Maximum Element-Sum of a Complete Subset of Indices/README.md
index 07cd5e3b2d88b..519a74a38a5a2 100644
--- a/solution/2800-2899/2862.Maximum Element-Sum of a Complete Subset of Indices/README.md
+++ b/solution/2800-2899/2862.Maximum Element-Sum of a Complete Subset of Indices/README.md
@@ -35,7 +35,7 @@ tags:
解释:
-我们选择下标为 2 和 8 的元素,并且 1 * 4 是一个完全平方数。
+我们选择下标为 2 和 8 的元素,并且 2 * 8 是一个完全平方数。
示例 2:
diff --git a/solution/3100-3199/3173.Bitwise OR of Adjacent Elements/README.md b/solution/3100-3199/3173.Bitwise OR of Adjacent Elements/README.md
index 321e2d876c4e6..8383b3574a1a9 100644
--- a/solution/3100-3199/3173.Bitwise OR of Adjacent Elements/README.md
+++ b/solution/3100-3199/3173.Bitwise OR of Adjacent Elements/README.md
@@ -9,7 +9,7 @@ tags:
-# [3173. 相邻元素的按位与 🔒](https://leetcode.cn/problems/bitwise-or-of-adjacent-elements)
+# [3173. 相邻元素的按位或 🔒](https://leetcode.cn/problems/bitwise-or-of-adjacent-elements)
[English Version](/solution/3100-3199/3173.Bitwise%20OR%20of%20Adjacent%20Elements/README_EN.md)
diff --git a/solution/3100-3199/3183.The Number of Ways to Make the Sum/README.md b/solution/3100-3199/3183.The Number of Ways to Make the Sum/README.md
index 2f53d2953a707..482b2d62e3c1f 100644
--- a/solution/3100-3199/3183.The Number of Ways to Make the Sum/README.md
+++ b/solution/3100-3199/3183.The Number of Ways to Make the Sum/README.md
@@ -6,7 +6,7 @@ edit_url: https://github.com/doocs/leetcode/edit/main/solution/3100-3199/3183.Th
-# [3183. The Number of Ways to Make the Sum 🔒](https://leetcode.cn/problems/the-number-of-ways-to-make-the-sum)
+# [3183. 达到总和的方法数量 🔒](https://leetcode.cn/problems/the-number-of-ways-to-make-the-sum)
[English Version](/solution/3100-3199/3183.The%20Number%20of%20Ways%20to%20Make%20the%20Sum/README_EN.md)
@@ -14,53 +14,55 @@ edit_url: https://github.com/doocs/leetcode/edit/main/solution/3100-3199/3183.Th
-You have an infinite number of coins with values 1, 2, and 6, and only 2 coins with value 4.
+给定 无限 数量的面值为 1,2,6 的硬币,并且 只有 2 枚硬币面值为 4。
-Given an integer n, return the number of ways to make the sum of n with the coins you have.
+给定一个整数 n ,返回用你持有的硬币达到总和 n 的方法数量。
-Since the answer may be very large, return it modulo 109 + 7.
+因为答案可能会很大,将其 取模 109 + 7。
-Note that the order of the coins doesn't matter and [2, 2, 3] is the same as [2, 3, 2].
+注意 硬币的顺序并不重要,[2, 2, 3] 与 [2, 3, 2] 相同。
-Example 1:
+
+示例 1:
-
Input: n = 4
+
输入:n = 4
-
Output: 4
+
输出:4
-
Explanation:
+
解释:
-
Here are the four combinations: [1, 1, 1, 1], [1, 1, 2], [2, 2], [4].
+
有四种组合:[1, 1, 1, 1],[1, 1, 2],[2, 2],[4]。
Example 2:
+示例 2:
-
Input: n = 12
+
输入:n = 12
-
Output: 22
+
输出:22
-
Explanation:
+
解释:
-
Note that [4, 4, 4] is not a valid combination since we cannot use 4 three times.
+
注意 [4, 4, 4] 不是 一个有效的组合,因为我们无法使用 4 三次。
Example 3:
+示例 3:
-
Input: n = 5
+
输入:n = 5
-
Output: 4
+
输出:4
-
Explanation:
+
解释:
-
Here are the four combinations: [1, 1, 1, 1, 1], [1, 1, 1, 2], [1, 2, 2], [1, 4].
+
有四种组合:[1, 1, 1, 1, 1],[1, 1, 1, 2],[1, 2, 2],[1, 4]。
-Constraints:
+
+提示:
1 <= n <= 105


