diff --git a/solution/2800-2899/2839.Check if Strings Can be Made Equal With Operations I/README.md b/solution/2800-2899/2839.Check if Strings Can be Made Equal With Operations I/README.md
index 405b0d747f6a2..1f8a4bbc5f97e 100644
--- a/solution/2800-2899/2839.Check if Strings Can be Made Equal With Operations I/README.md
+++ b/solution/2800-2899/2839.Check if Strings Can be Made Equal With Operations I/README.md
@@ -49,6 +49,18 @@
+**方法一:计数**
+
+我们观察题目中的操作,可以发现,如果字符串的两个下标 $i$ 和 $j$ 的奇偶性相同,那么它们可以通过交换改变顺序。
+
+因此,我们可以统计两个字符串中奇数下标的字符的出现次数,以及偶数下标的字符的出现次数,如果两个字符串的统计结果相同,那么我们就可以通过操作使得两个字符串相等。
+
+时间复杂度 $O(n + |\Sigma|)$,空间复杂度 $O(|\Sigma|)$。其中 $n$ 是字符串的长度,而 $\Sigma$ 是字符集。
+
+相似题目:
+
+- [2840. 判断通过操作能否让字符串相等 II](/solution/2800-2899/2840.Check%20if%20Strings%20Can%20be%20Made%20Equal%20With%20Operations%20II/README.md)
+
### **Python3**
diff --git a/solution/2800-2899/2840.Check if Strings Can be Made Equal With Operations II/README.md b/solution/2800-2899/2840.Check if Strings Can be Made Equal With Operations II/README.md
index 83b366ae08feb..41ad0711cf091 100644
--- a/solution/2800-2899/2840.Check if Strings Can be Made Equal With Operations II/README.md
+++ b/solution/2800-2899/2840.Check if Strings Can be Made Equal With Operations II/README.md
@@ -55,6 +55,18 @@
+**方法一:计数**
+
+我们观察题目中的操作,可以发现,如果字符串的两个下标 $i$ 和 $j$ 的奇偶性相同,那么它们可以通过交换改变顺序。
+
+因此,我们可以统计两个字符串中奇数下标的字符的出现次数,以及偶数下标的字符的出现次数,如果两个字符串的统计结果相同,那么我们就可以通过操作使得两个字符串相等。
+
+时间复杂度 $O(n + |\Sigma|)$,空间复杂度 $O(|\Sigma|)$。其中 $n$ 是字符串的长度,而 $\Sigma$ 是字符集。
+
+相似题目:
+
+- [2839. 判断通过操作能否让字符串相等 I](/solution/2800-2899/2839.Check%20if%20Strings%20Can%20be%20Made%20Equal%20With%20Operations%20I/README.md)
+
### **Python3**
diff --git a/solution/2800-2899/2841.Maximum Sum of Almost Unique Subarray/README.md b/solution/2800-2899/2841.Maximum Sum of Almost Unique Subarray/README.md
index e331d25a912db..ebb49a5379a86 100644
--- a/solution/2800-2899/2841.Maximum Sum of Almost Unique Subarray/README.md
+++ b/solution/2800-2899/2841.Maximum Sum of Almost Unique Subarray/README.md
@@ -54,6 +54,14 @@
+**方法一:滑动窗口 + 哈希表**
+
+我们可以遍历数组 $nums$,维护一个大小为 $k$ 的窗口,用哈希表 $cnt$ 统计窗口中每个元素的出现次数,用变量 $s$ 统计窗口中所有元素的和。如果 $cnt$ 中不同元素的个数大于等于 $m$,那么我们就更新答案 $ans = \max(ans, s)$。
+
+遍历结束后,返回答案即可。
+
+时间复杂度 $O(n)$,空间复杂度 $O(k)$。其中 $n$ 是数组的长度。
+
### **Python3**
diff --git a/solution/2800-2899/2842.Count K-Subsequences of a String With Maximum Beauty/README.md b/solution/2800-2899/2842.Count K-Subsequences of a String With Maximum Beauty/README.md
index 334de9440cdda..c899c7fcb62ec 100644
--- a/solution/2800-2899/2842.Count K-Subsequences of a String With Maximum Beauty/README.md
+++ b/solution/2800-2899/2842.Count K-Subsequences of a String With Maximum Beauty/README.md
@@ -83,6 +83,22 @@ s 的 k 子序列为:
+**方法一:贪心 + 组合数学**
+
+我们先用哈希表 $f$ 统计字符串 $s$ 中每个字符的出现次数,即 $f[c]$ 表示字符 $c$ 在字符串 $s$ 中出现的次数。
+
+由于 $k$ 子序列是字符串 $s$ 中一个长度为 $k$ 的子序列,且字符唯一,因此,如果 $f$ 中不同字符的个数小于 $k$,那么不存在 $k$ 子序列,直接返回 $0$ 即可。
+
+否则,要使得 $k$ 子序列的美丽值最大,我们需要尽可能地让美丽值大的字符尽可能地多地出现在 $k$ 子序列中。因此,我们可以对 $f$ 中的值进行倒序排序,得到一个数组 $vs$。
+
+我们记数组 $vs$ 第 $k$ 个字符的出现次数为 $val$,一共有 $x$ 个字符出现的次数为 $val$。
+
+那么我们先找出出现次数大于 $val$ 的字符,将每个字符出现的次数相乘,得到初始答案 $ans$,剩余的需要选取的字符个数更新为 $k$。我们需要从 $x$ 个字符中选取 $k$ 个字符,因此答案需要乘上组合数 $C_x^k$,最后再乘上 $val^k$,即 $ans = ans \times C_x^k \times val^k$。
+
+注意,这里需要用到快速幂,以及取模操作。
+
+时间复杂度 $O(n)$,空间复杂度 $O(|\Sigma|)$。其中 $n$ 是字符串的长度,而 $\Sigma$ 是字符集。本题中字符集为小写字母,因此 $|\Sigma| = 26$。
+
### **Python3**
diff --git a/solution/2800-2899/2843.Count Symmetric Integers/README.md b/solution/2800-2899/2843.Count Symmetric Integers/README.md
index 64413585ec6ae..b728385b2c366 100644
--- a/solution/2800-2899/2843.Count Symmetric Integers/README.md
+++ b/solution/2800-2899/2843.Count Symmetric Integers/README.md
@@ -42,6 +42,12 @@
+**方法一:枚举**
+
+我们枚举 $[low, high]$ 中的每个整数 $x$,判断其是否是对称整数。如果是,那么答案 $ans$ 增加 $1$。
+
+时间复杂度 $O(n \times \log m)$,空间复杂度 $O(\log m)$。其中 $n$ 是 $[low, high]$ 中整数的个数,而 $m$ 是题目中给出的最大整数。
+
### **Python3**
diff --git a/solution/2800-2899/2844.Minimum Operations to Make a Special Number/README.md b/solution/2800-2899/2844.Minimum Operations to Make a Special Number/README.md
index d3d2421456637..096dd8e85ea1d 100644
--- a/solution/2800-2899/2844.Minimum Operations to Make a Special Number/README.md
+++ b/solution/2800-2899/2844.Minimum Operations to Make a Special Number/README.md
@@ -57,6 +57,19 @@
+**方法一:记忆化搜索**
+
+我们注意到,整数 $x$ 要能被 $25$ 整除,即 $x \bmod 25 = 0$。因此,我们可以设计一个函数 $dfs(i, k)$,表示从字符串 $num$ 的第 $i$ 位开始,且当前数字模 $25$ 的结果为 $k$ 的情况下,要使得数字变成特殊数字,最少需要删除多少位数字。那么答案为 $dfs(0, 0)$。
+
+函数 $dfs(i, k)$ 的执行逻辑如下:
+
+- 如果 $i = n$,即已经处理完字符串 $num$ 的所有位,那么如果 $k = 0$,则当前数字可以被 $25$ 整除,返回 $0$,否则返回 $n$;
+- 否则,第 $i$ 位可以被删除,此时需要删除一位,即 $dfs(i + 1, k) + 1$;第 $i$ 位不删除,那么 $k$ 的值变为 $(k \times 10 + \textit{num}[i]) \bmod 25$,即 $dfs(i + 1, (k \times 10 + \textit{num}[i]) \bmod 25)$。取这两者的最小值即可。
+
+为了防止重复计算,我们可以使用记忆化的方法优化时间复杂度。
+
+时间复杂度 $O(n \times 25)$,空间复杂度 $O(n \times 25)$。其中 $n$ 是字符串 $num$ 的长度。
+
### **Python3**
diff --git a/solution/2800-2899/2845.Count of Interesting Subarrays/README.md b/solution/2800-2899/2845.Count of Interesting Subarrays/README.md
index 6b6dded2576c1..6a63cb3545829 100644
--- a/solution/2800-2899/2845.Count of Interesting Subarrays/README.md
+++ b/solution/2800-2899/2845.Count of Interesting Subarrays/README.md
@@ -68,6 +68,20 @@
+**方法一:哈希表 + 前缀和**
+
+题目要求一个区间内满足 $nums[i] \bmod modulo = k$ 的索引 $i$ 的数量,我们可以将数组 $nums$ 转换为一个 $0-1$ 数组 $arr$,其中 $arr[i] = 1$ 表示 $nums[i] \bmod modulo = k$,否则 $arr[i] = 0$。
+
+那么对于一个区间 $[l, r]$,我们可以通过前缀和数组 $s$ 来计算 $arr[l..r]$ 中 $1$ 的数量,即 $s[r] - s[l - 1]$,其中 $s[0] = 0$。
+
+我们用哈希表 $cnt$ 记录前缀和 $s \bmod modulo$ 出现的次数,初始时 $cnt[0]=1$。
+
+接下来,我们遍历数组 $arr$,计算前缀和 $s$,将 $(s-k) \bmod modulo$ 出现的次数累加到答案中,然后将 $s \bmod modulo$ 出现的次数加 $1$。
+
+遍历结束后,返回答案即可。
+
+时间复杂度 $O(n)$,空间复杂度 $O(n)$。其中 $n$ 是数组 $nums$ 的长度。
+
### **Python3**
diff --git a/solution/2800-2899/2846.Minimum Edge Weight Equilibrium Queries in a Tree/README.md b/solution/2800-2899/2846.Minimum Edge Weight Equilibrium Queries in a Tree/README.md
index f861d73185536..3f3dbb20e771a 100644
--- a/solution/2800-2899/2846.Minimum Edge Weight Equilibrium Queries in a Tree/README.md
+++ b/solution/2800-2899/2846.Minimum Edge Weight Equilibrium Queries in a Tree/README.md
@@ -22,7 +22,7 @@
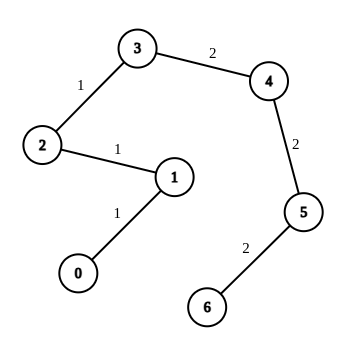
示例 1:
- +
+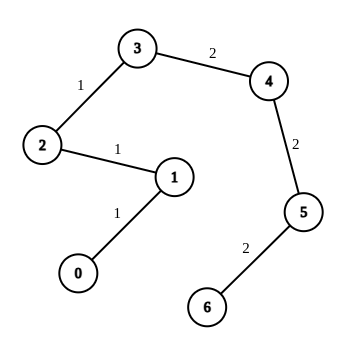
输入:n = 7, edges = [[0,1,1],[1,2,1],[2,3,1],[3,4,2],[4,5,2],[5,6,2]], queries = [[0,3],[3,6],[2,6],[0,6]]
输出:[0,0,1,3]
@@ -34,7 +34,7 @@
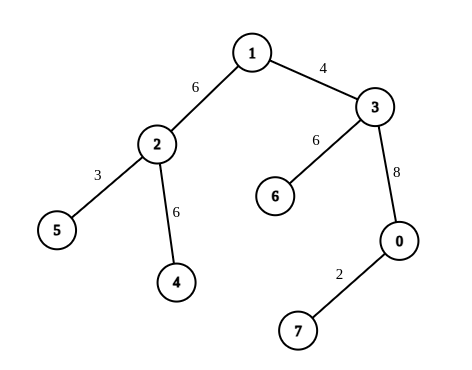
示例 2:
- +
+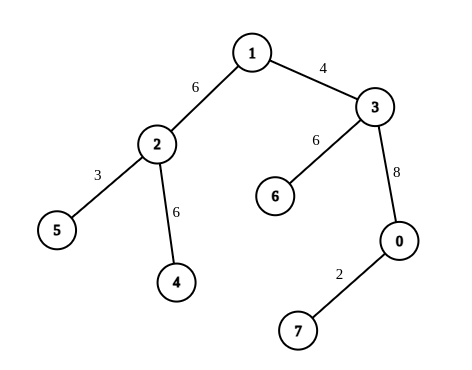
输入:n = 8, edges = [[1,2,6],[1,3,4],[2,4,6],[2,5,3],[3,6,6],[3,0,8],[7,0,2]], queries = [[4,6],[0,4],[6,5],[7,4]]
输出:[1,2,2,3]
diff --git a/solution/2800-2899/2846.Minimum Edge Weight Equilibrium Queries in a Tree/README_EN.md b/solution/2800-2899/2846.Minimum Edge Weight Equilibrium Queries in a Tree/README_EN.md
index 6371893f83b89..6da91c35cab9d 100644
--- a/solution/2800-2899/2846.Minimum Edge Weight Equilibrium Queries in a Tree/README_EN.md
+++ b/solution/2800-2899/2846.Minimum Edge Weight Equilibrium Queries in a Tree/README_EN.md
@@ -19,7 +19,7 @@
Example 1:
- +
+
Input: n = 7, edges = [[0,1,1],[1,2,1],[2,3,1],[3,4,2],[4,5,2],[5,6,2]], queries = [[0,3],[3,6],[2,6],[0,6]]
Output: [0,0,1,3]
@@ -31,7 +31,7 @@ For each queries[i], it can be shown that answer[i] is the minimum number of ope
Example 2:
- +
+
Input: n = 8, edges = [[1,2,6],[1,3,4],[2,4,6],[2,5,3],[3,6,6],[3,0,8],[7,0,2]], queries = [[4,6],[0,4],[6,5],[7,4]]
Output: [1,2,2,3]
diff --git a/solution/2800-2899/2846.Minimum Edge Weight Equilibrium Queries in a Tree/images/graph-6-1.png b/solution/2800-2899/2846.Minimum Edge Weight Equilibrium Queries in a Tree/images/graph-6-1.png
new file mode 100644
index 0000000000000..b7b30145b8989
Binary files /dev/null and b/solution/2800-2899/2846.Minimum Edge Weight Equilibrium Queries in a Tree/images/graph-6-1.png differ
diff --git a/solution/2800-2899/2846.Minimum Edge Weight Equilibrium Queries in a Tree/images/graph-9-1.png b/solution/2800-2899/2846.Minimum Edge Weight Equilibrium Queries in a Tree/images/graph-9-1.png
new file mode 100644
index 0000000000000..336bd84d5ef6c
Binary files /dev/null and b/solution/2800-2899/2846.Minimum Edge Weight Equilibrium Queries in a Tree/images/graph-9-1.png differ
 +
+
 +
+