Given two integer arrays inorder and postorder where inorder is the inorder traversal of a binary tree and postorder is the postorder traversal of the same tree, construct and return the binary tree.
Example 1:
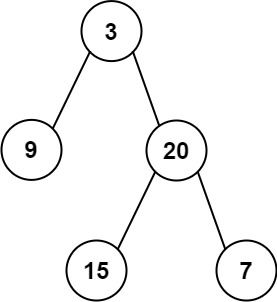
Input: inorder = [9,3,15,20,7], postorder = [9,15,7,20,3] Output: [3,9,20,null,null,15,7]
Example 2:
Input: inorder = [-1], postorder = [-1] Output: [-1]
Constraints:
1 <= inorder.length <= 3000postorder.length == inorder.length-3000 <= inorder[i], postorder[i] <= 3000inorderandpostorderconsist of unique values.- Each value of
postorderalso appears ininorder. inorderis guaranteed to be the inorder traversal of the tree.postorderis guaranteed to be the postorder traversal of the tree.
The approach is the same as in 105. Construct Binary Tree from Preorder and Inorder Traversal.
The time complexity is
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
if not postorder:
return None
v = postorder[-1]
root = TreeNode(val=v)
i = inorder.index(v)
root.left = self.buildTree(inorder[:i], postorder[:i])
root.right = self.buildTree(inorder[i + 1 :], postorder[i:-1])
return root/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
private Map<Integer, Integer> indexes = new HashMap<>();
public TreeNode buildTree(int[] inorder, int[] postorder) {
for (int i = 0; i < inorder.length; ++i) {
indexes.put(inorder[i], i);
}
return dfs(inorder, postorder, 0, 0, inorder.length);
}
private TreeNode dfs(int[] inorder, int[] postorder, int i, int j, int n) {
if (n <= 0) {
return null;
}
int v = postorder[j + n - 1];
int k = indexes.get(v);
TreeNode root = new TreeNode(v);
root.left = dfs(inorder, postorder, i, j, k - i);
root.right = dfs(inorder, postorder, k + 1, j + k - i, n - k + i - 1);
return root;
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
unordered_map<int, int> indexes;
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
for (int i = 0; i < inorder.size(); ++i) indexes[inorder[i]] = i;
return dfs(inorder, postorder, 0, 0, inorder.size());
}
TreeNode* dfs(vector<int>& inorder, vector<int>& postorder, int i, int j, int n) {
if (n <= 0) return nullptr;
int v = postorder[j + n - 1];
int k = indexes[v];
TreeNode* root = new TreeNode(v);
root->left = dfs(inorder, postorder, i, j, k - i);
root->right = dfs(inorder, postorder, k + 1, j + k - i, n - k + i - 1);
return root;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func buildTree(inorder []int, postorder []int) *TreeNode {
indexes := make(map[int]int)
for i, v := range inorder {
indexes[v] = i
}
var dfs func(i, j, n int) *TreeNode
dfs = func(i, j, n int) *TreeNode {
if n <= 0 {
return nil
}
v := postorder[j+n-1]
k := indexes[v]
root := &TreeNode{Val: v}
root.Left = dfs(i, j, k-i)
root.Right = dfs(k+1, j+k-i, n-k+i-1)
return root
}
return dfs(0, 0, len(inorder))
}/**
* Definition for a binary tree node.
* class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
function buildTree(inorder: number[], postorder: number[]): TreeNode | null {
const n = postorder.length;
if (n == 0) {
return null;
}
const val = postorder[n - 1];
const index = inorder.indexOf(val);
return new TreeNode(
val,
buildTree(inorder.slice(0, index), postorder.slice(0, index)),
buildTree(inorder.slice(index + 1), postorder.slice(index, n - 1)),
);
}// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
// pub val: i32,
// pub left: Option<Rc<RefCell<TreeNode>>>,
// pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
// #[inline]
// pub fn new(val: i32) -> Self {
// TreeNode {
// val,
// left: None,
// right: None
// }
// }
// }
use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
fn reset(
inorder: &Vec<i32>,
i_left: usize,
i_right: usize,
postorder: &Vec<i32>,
p_left: usize,
p_right: usize
) -> Option<Rc<RefCell<TreeNode>>> {
if i_left == i_right {
return None;
}
let val = postorder[p_right - 1];
let index = inorder
.iter()
.position(|&v| v == val)
.unwrap();
Some(
Rc::new(
RefCell::new(TreeNode {
val,
left: Self::reset(
inorder,
i_left,
index,
postorder,
p_left,
p_left + index - i_left
),
right: Self::reset(
inorder,
index + 1,
i_right,
postorder,
p_left + index - i_left,
p_right - 1
),
})
)
)
}
pub fn build_tree(inorder: Vec<i32>, postorder: Vec<i32>) -> Option<Rc<RefCell<TreeNode>>> {
let n = inorder.len();
Self::reset(&inorder, 0, n, &postorder, 0, n)
}
}