README.md

230. 二叉搜索树中第 K 小的元素

English Version

题目描述

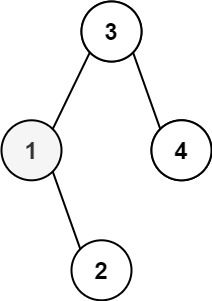
给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

 

示例 1：

输入：root = [3,1,4,null,2], k = 1
输出：1

示例 2：

输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3

 

 

提示：

• 树中的节点数为 n 。
• 1 <= k <= n <= 104
• 0 <= Node.val <= 104

 

进阶：如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

解法

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
        def dfs(root):
            if root:
                nonlocal k, ans
                dfs(root.left)
                k -= 1
                if k == 0:
                    ans = root.val
                    return
                dfs(root.right)

        ans = -1
        dfs(root)
        return ans

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int k;
    private int ans;

    public int kthSmallest(TreeNode root, int k) {
        this.k = k;
        dfs(root);
        return ans;
    }

    private void dfs(TreeNode root) {
        if (root == null) {
            return;
        }
        dfs(root.left);
        if (--k == 0) {
            ans = root.val;
            return;
        }
        dfs(root.right);
    }
}

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int kthSmallest(TreeNode root, int k) {
        int ans = -1;
        while (root != null) {
            if (root.left == null) {
                --k;
                if (k == 0) {
                    ans = root.val;
                    return ans;
                }
                root = root.right;
            } else {
                TreeNode pre = root.left;
                while (pre.right != null && pre.right != root) {
                    pre = pre.right;
                }
                if (pre.right == null) {
                    pre.right = root;
                    root = root.left;
                } else {
                    --k;
                    if (k == 0) {
                        ans = root.val;
                        return ans;
                    }
                    pre.right = null;
                    root = root.right;
                }
            }
        }
        return ans;
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int k;
    int ans;

    int kthSmallest(TreeNode* root, int k) {
        this->k = k;
        dfs(root);
        return ans;
    }

    void dfs(TreeNode* root) {
        if (!root) return;
        dfs(root->left);
        if (--k == 0)
        {
            ans = root->val;
            return;
        }
        dfs(root->right);
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func kthSmallest(root *TreeNode, k int) int {
	var ans int

	var dfs func(root *TreeNode)
	dfs = func(root *TreeNode) {
		if root != nil {
			dfs(root.Left)
			k--
			if k == 0 {
				ans = root.Val
				return
			}
			dfs(root.Right)
		}
	}

	dfs(root)
	return ans
}

TypeScript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function kthSmallest(root: TreeNode | null, k: number): number {
    const dfs = (root: TreeNode | null) => {
        if (root == null) {
            return -1;
        }
        const { val, left, right } = root;
        const l = dfs(left);
        if (l !== -1) {
            return l;
        }
        k--;
        if (k === 0) {
            return val;
        }
        return dfs(right);
    };
    return dfs(root);
}

Rust

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
    fn dfs(root: Option<Rc<RefCell<TreeNode>>>, res: &mut Vec<i32>, k: usize) {
        if let Some(node) = root {
            let mut node = node.borrow_mut();
            Self::dfs(node.left.take(), res, k);
            res.push(node.val);
            if res.len() >= k {
                return;
            }
            Self::dfs(node.right.take(), res, k);
        }
    }
    pub fn kth_smallest(root: Option<Rc<RefCell<TreeNode>>>, k: i32) -> i32 {
        let k = k as usize;
        let mut res: Vec<i32> = Vec::with_capacity(k);
        Self::dfs(root, &mut res, k);
        res[k - 1]
    }
}

...