README.md

119. 杨辉三角 II

English Version

题目描述

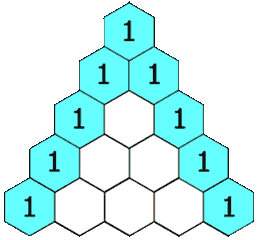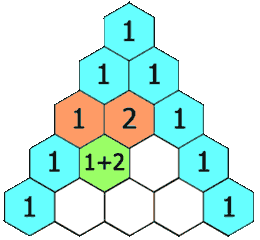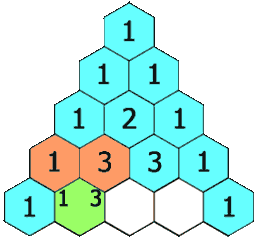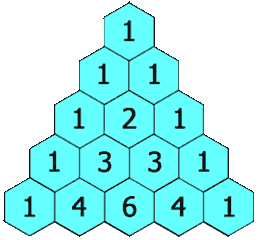
给定一个非负索引 k，其中 k ≤ 33，返回杨辉三角的第 k 行。

在杨辉三角中，每个数是它左上方和右上方的数的和。

示例:

输入: 3
输出: [1,3,3,1]

进阶：

你可以优化你的算法到 O(k) 空间复杂度吗？

解法

Python3

class Solution:
    def getRow(self, rowIndex: int) -> List[int]:
        def makePascal(prevArr):
            if len(prevArr) == 0:
                return [1]
            elif len(prevArr) == 1:
                return [1, 1]
            else:
                NewArr = [0] * (len(prevArr) + 1)
                NewArr[0], NewArr[-1] = 1, 1
                for i in range(len(prevArr) - 1):
                    NewArr[i + 1] = prevArr[i] + prevArr[i + 1]
                return NewArr

        temp = []
        Pascal = []
        for i in range(rowIndex + 1):
            temp = makePascal(temp)
            Pascal.append(temp)
        return Pascal[rowIndex]

Java

class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<Integer> ret = new LinkedList<>();
        long nk = 1;
        for (int i = 0; i <= rowIndex; i++) {
            ret.add((int) nk);
            nk = nk * (rowIndex - i) / (i + 1);
        }
        return ret;
    }
}

Go

func getRow(rowIndex int) []int {
	row := make([]int, rowIndex+1)
	row[0] = 1
	for i := 1; i <= rowIndex; i++ {
		for j := i; j > 0; j-- {
			row[j] += row[j-1]
		}
	}
	return row
}

...