Given the root of a binary tree, return the maximum width of the given tree.
The maximum width of a tree is the maximum width among all levels.
The width of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes are also counted into the length calculation.
It is guaranteed that the answer will in the range of 32-bit signed integer.
Example 1:
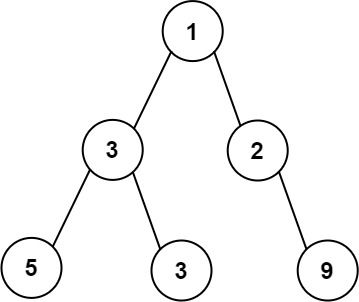
Input: root = [1,3,2,5,3,null,9] Output: 4 Explanation: The maximum width existing in the third level with the length 4 (5,3,null,9).
Example 2:
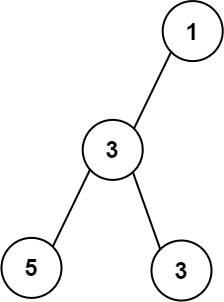
Input: root = [1,3,null,5,3] Output: 2 Explanation: The maximum width existing in the third level with the length 2 (5,3).
Example 3:
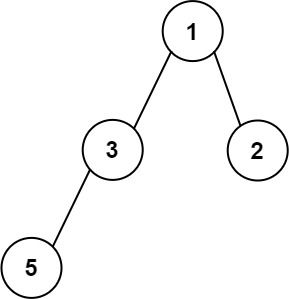
Input: root = [1,3,2,5] Output: 2 Explanation: The maximum width existing in the second level with the length 2 (3,2).
Example 4:
Input: root = [1,3,2,5,null,null,9,6,null,null,7] Output: 8 Explanation: The maximum width existing in the fourth level with the length 8 (6,null,null,null,null,null,null,7).
Constraints:
- The number of nodes in the tree is in the range
[1, 3000]. -100 <= Node.val <= 100
BFS.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def widthOfBinaryTree(self, root: TreeNode) -> int:
q = deque([(root, 1)])
ans = 0
while q:
n = len(q)
ans = max(ans, q[-1][1] - q[0][1] + 1)
for _ in range(n):
node, j = q.popleft()
if node.left:
q.append((node.left, 2 * j))
if node.right:
q.append((node.right, 2 * j + 1))
return ans/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int widthOfBinaryTree(TreeNode root) {
Deque<Pair<TreeNode, Integer>> q = new ArrayDeque<>();
q.offerLast(new Pair<>(root, 1));
int ans = 0;
while (!q.isEmpty()) {
ans = Math.max(ans, q.peekLast().getValue() - q.peekFirst().getValue() + 1);
for (int i = 0, n = q.size(); i < n; ++i) {
Pair<TreeNode, Integer> node = q.pollFirst();
if (node.getKey().left != null) {
q.offerLast(new Pair<>(node.getKey().left, node.getValue() * 2));
}
if (node.getKey().right != null) {
q.offerLast(new Pair<>(node.getKey().right, node.getValue() * 2 + 1));
}
}
}
return ans;
}
}/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int widthOfBinaryTree(TreeNode* root) {
queue<pair<TreeNode*, int>> q;
q.emplace(root, 1);
int ans = 0;
while (!q.empty())
{
ans = max(ans, q.back().second - q.front().second + 1);
int start = q.front().second;
for (int i = 0, n = q.size(); i < n; ++i)
{
auto node = q.front();
q.pop();
if (node.first->left != nullptr) q.emplace(node.first->left, node.second * 2 - start * 2);
if (node.first->right != nullptr) q.emplace(node.first->right, node.second * 2 + 1 - start * 2);
}
}
return ans;
}
};/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
type Node struct {
node *TreeNode
idx int
}
func widthOfBinaryTree(root *TreeNode) int {
q := []Node{{root, 1}}
ans := 0
for len(q) > 0 {
ans = max(ans, q[len(q)-1].idx-q[0].idx+1)
n := len(q)
for i := 0; i < n; i++ {
node := q[0]
q = q[1:]
if node.node.Left != nil {
q = append(q, Node{node.node.Left, node.idx * 2})
}
if node.node.Right != nil {
q = append(q, Node{node.node.Right, node.idx*2 + 1})
}
}
}
return ans
}
func max(a, b int) int {
if a > b {
return a
}
return b
}