README_EN.md

130. Surrounded Regions

中文文档

Description

Given an m x n matrix board containing 'X' and 'O', capture all regions surrounded by 'X'.

A region is captured by flipping all 'O's into 'X's in that surrounded region.

 

Example 1:

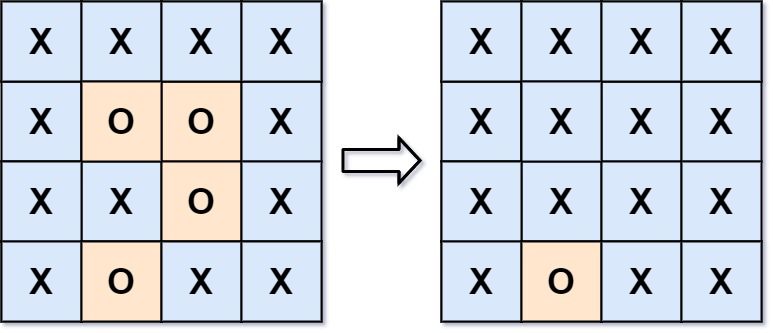
Input: board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
Output: [["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
Explanation: Surrounded regions should not be on the border, which means that any 'O' on the border of the board are not flipped to 'X'. Any 'O' that is not on the border and it is not connected to an 'O' on the border will be flipped to 'X'. Two cells are connected if they are adjacent cells connected horizontally or vertically.

Example 2:

Input: board = [["X"]]
Output: [["X"]]

 

Constraints:

• m == board.length
• n == board[i].length
• 1 <= m, n <= 200
• board[i][j] is 'X' or 'O'.

Solutions

Python3

Java

TypeScript

/**
 Do not return anything, modify board in-place instead.
 */
function solve(board: string[][]): void {
    let m = board.length, n = board[0].length;
    if (m < 3 || n < 3) return;
    let visited = Array.from({ length: m }, v => new Array(n).fill(false));
    // 第一行，最后一行， 第一列， 最后一列
    for (let i of [0, m-1]) {
        for (let j = 0; j < n; ++j) {
            if (board[i][j] == 'X') {
                visited[i][j] = true;
            } else {
                dfs(board, i, j, visited, true);
            }
        }
    }
    for (let i = 0; i < m; ++i) {
        for (let j of [0, n - 1]) {
            if (board[i][j] == 'X') {
                visited[i][j] = true;
            } else {
                dfs(board, i, j, visited, true);
            }
        }
    }
    for (let i = 1; i < m - 1; ++i) {
        for (let j = 1; j < n - 1; ++j) {
            !visited[i][j] && dfs(board, i, j, visited);
        }
    }
};

function dfs(board: string[][], i: number, j: number, visited: boolean[][], edge = false): void {
    let m = board.length, n = board[0].length;
    if (i < 0 || i > m - 1 || j < 0 || j > n - 1 || visited[i][j]) {
        return;
    }

    visited[i][j] = true;
    if (board[i][j] == 'X') {
        return;
    }
    if (!edge) {
        board[i][j] = 'X';
    }
    for (let [dx, dy] of [[0, 1], [0, -1], [1, 0], [-1, 0]]) {
        let x = i + dx, y = j + dy;
        dfs(board, x, y, visited, edge);
    }
}

...