README_EN.md

comments	difficulty	edit_url	tags
true	Medium	https://github.com/doocs/leetcode/edit/main/solution/0000-0099/0059.Spiral%20Matrix%20II/README_EN.md	Array Matrix Simulation

59. Spiral Matrix II

中文文档

Description

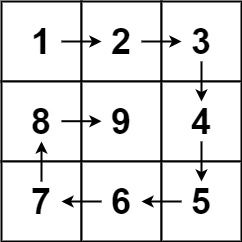
Given a positive integer n, generate an n x n matrix filled with elements from 1 to n2 in spiral order.

 

Example 1:

Input: n = 3
Output: [[1,2,3],[8,9,4],[7,6,5]]

Example 2:

Input: n = 1
Output: [[1]]

 

Constraints:

• 1 <= n <= 20

Solutions

Solution 1: Simulation

We can directly simulate the process of generating the spiral matrix.

Define a 2D array $\textit{ans}$ to store the spiral matrix. Use $i$ and $j$ to represent the current row and column indices, and use $k$ to represent the current direction index. $\textit{dirs}$ represents the mapping between direction indices and directions.

Starting from $1$, fill each position in the matrix sequentially. After filling a position, calculate the row and column indices of the next position. If the next position is out of bounds or has already been filled, change the direction and then calculate the row and column indices of the next position.

The time complexity is $O(n^2)$, where $n$ is the side length of the matrix. Ignoring the space consumption of the answer array, the space complexity is $O(1)$.

Python3

class Solution:
    def generateMatrix(self, n: int) -> List[List[int]]:
        ans = [[0] * n for _ in range(n)]
        dirs = (0, 1, 0, -1, 0)
        i = j = k = 0
        for v in range(1, n * n + 1):
            ans[i][j] = v
            x, y = i + dirs[k], j + dirs[k + 1]
            if x < 0 or x >= n or y < 0 or y >= n or ans[x][y]:
                k = (k + 1) % 4
            i, j = i + dirs[k], j + dirs[k + 1]
        return ans

Java

class Solution {
    public int[][] generateMatrix(int n) {
        int[][] ans = new int[n][n];
        final int[] dirs = {0, 1, 0, -1, 0};
        int i = 0, j = 0, k = 0;
        for (int v = 1; v <= n * n; ++v) {
            ans[i][j] = v;
            int x = i + dirs[k], y = j + dirs[k + 1];
            if (x < 0 || x >= n || y < 0 || y >= n || ans[x][y] != 0) {
                k = (k + 1) % 4;
            }
            i += dirs[k];
            j += dirs[k + 1];
        }
        return ans;
    }
}

C++

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> ans(n, vector<int>(n, 0));
        const int dirs[5] = {0, 1, 0, -1, 0};
        int i = 0, j = 0, k = 0;
        for (int v = 1; v <= n * n; ++v) {
            ans[i][j] = v;
            int x = i + dirs[k], y = j + dirs[k + 1];
            if (x < 0 || x >= n || y < 0 || y >= n || ans[x][y] != 0) {
                k = (k + 1) % 4;
            }
            i += dirs[k];
            j += dirs[k + 1];
        }
        return ans;
    }
};

Go

func generateMatrix(n int) [][]int {
	ans := make([][]int, n)
	for i := range ans {
		ans[i] = make([]int, n)
	}
	dirs := [5]int{0, 1, 0, -1, 0}
	i, j, k := 0, 0, 0
	for v := 1; v <= n*n; v++ {
		ans[i][j] = v
		x, y := i+dirs[k], j+dirs[k+1]
		if x < 0 || x >= n || y < 0 || y >= n || ans[x][y] != 0 {
			k = (k + 1) % 4
		}
		i += dirs[k]
		j += dirs[k+1]
	}
	return ans
}

TypeScript

function generateMatrix(n: number): number[][] {
    const ans: number[][] = Array.from({ length: n }, () => Array(n).fill(0));
    const dirs = [0, 1, 0, -1, 0];
    let [i, j, k] = [0, 0, 0];
    for (let v = 1; v <= n * n; v++) {
        ans[i][j] = v;
        const [x, y] = [i + dirs[k], j + dirs[k + 1]];
        if (x < 0 || x >= n || y < 0 || y >= n || ans[x][y] !== 0) {
            k = (k + 1) % 4;
        }
        i += dirs[k];
        j += dirs[k + 1];
    }
    return ans;
}

Rust

impl Solution {
    pub fn generate_matrix(n: i32) -> Vec<Vec<i32>> {
        let mut ans = vec![vec![0; n as usize]; n as usize];
        let dirs = [0, 1, 0, -1, 0];
        let (mut i, mut j, mut k) = (0, 0, 0);
        for v in 1..=n * n {
            ans[i as usize][j as usize] = v;
            let (x, y) = (i + dirs[k], j + dirs[k + 1]);
            if x < 0 || x >= n || y < 0 || y >= n || ans[x as usize][y as usize] != 0 {
                k = (k + 1) % 4;
            }
            i += dirs[k];
            j += dirs[k + 1];
        }
        ans
    }
}

JavaScript

/**
 * @param {number} n
 * @return {number[][]}
 */
var generateMatrix = function (n) {
    const ans = Array.from({ length: n }, () => Array(n).fill(0));
    const dirs = [0, 1, 0, -1, 0];
    let [i, j, k] = [0, 0, 0];
    for (let v = 1; v <= n * n; v++) {
        ans[i][j] = v;
        const [x, y] = [i + dirs[k], j + dirs[k + 1]];
        if (x < 0 || x >= n || y < 0 || y >= n || ans[x][y] !== 0) {
            k = (k + 1) % 4;
        }
        i += dirs[k];
        j += dirs[k + 1];
    }
    return ans;
};