Skip to content

Latest commit

 

History

History
229 lines (191 loc) · 5.79 KB

README_EN.md

File metadata and controls

229 lines (191 loc) · 5.79 KB
comments difficulty edit_url rating source tags
true
Medium
1648
Biweekly Contest 59 Q2
Greedy
Array
Matrix

1975. Maximum Matrix Sum

中文文档

Description

You are given an n x n integer matrix. You can do the following operation any number of times:

  • Choose any two adjacent elements of matrix and multiply each of them by -1.

Two elements are considered adjacent if and only if they share a border.

Your goal is to maximize the summation of the matrix's elements. Return the maximum sum of the matrix's elements using the operation mentioned above.

 

Example 1:

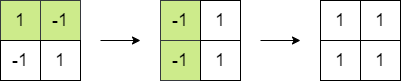
Input: matrix = [[1,-1],[-1,1]]
Output: 4
Explanation: We can follow the following steps to reach sum equals 4:
- Multiply the 2 elements in the first row by -1.
- Multiply the 2 elements in the first column by -1.

Example 2:

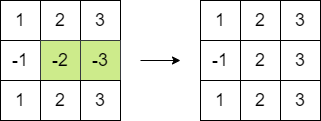
Input: matrix = [[1,2,3],[-1,-2,-3],[1,2,3]]
Output: 16
Explanation: We can follow the following step to reach sum equals 16:
- Multiply the 2 last elements in the second row by -1.

 

Constraints:

  • n == matrix.length == matrix[i].length
  • 2 <= n <= 250
  • -105 <= matrix[i][j] <= 105

Solutions

Solution 1: Greedy

If there is a zero in the matrix, or the number of negative numbers in the matrix is even, then the maximum sum is the sum of the absolute values of all elements in the matrix.

Otherwise, if there are an odd number of negative numbers in the matrix, there will be one negative number left in the end. We choose the number with the smallest absolute value and make it negative, so that the final sum is maximized.

The time complexity is $O(m \times n)$, where $m$ and $n$ are the number of rows and columns of the matrix, respectively. The space complexity is $O(1)$.

Python3

class Solution:
    def maxMatrixSum(self, matrix: List[List[int]]) -> int:
        mi = inf
        s = cnt = 0
        for row in matrix:
            for x in row:
                cnt += x < 0
                y = abs(x)
                mi = min(mi, y)
                s += y
        return s if cnt % 2 == 0 else s - mi * 2

Java

class Solution {
    public long maxMatrixSum(int[][] matrix) {
        long s = 0;
        int mi = 1 << 30, cnt = 0;
        for (var row : matrix) {
            for (int x : row) {
                cnt += x < 0 ? 1 : 0;
                int y = Math.abs(x);
                mi = Math.min(mi, y);
                s += y;
            }
        }
        return cnt % 2 == 0 ? s : s - mi * 2;
    }
}

C++

class Solution {
public:
    long long maxMatrixSum(vector<vector<int>>& matrix) {
        long long s = 0;
        int mi = 1 << 30, cnt = 0;
        for (const auto& row : matrix) {
            for (int x : row) {
                cnt += x < 0 ? 1 : 0;
                int y = abs(x);
                mi = min(mi, y);
                s += y;
            }
        }
        return cnt % 2 == 0 ? s : s - mi * 2;
    }
};

Go

func maxMatrixSum(matrix [][]int) int64 {
	var s int64
	mi, cnt := 1<<30, 0
	for _, row := range matrix {
		for _, x := range row {
			if x < 0 {
				cnt++
				x = -x
			}
			mi = min(mi, x)
			s += int64(x)
		}
	}
	if cnt%2 == 0 {
		return s
	}
	return s - int64(mi*2)
}

TypeScript

function maxMatrixSum(matrix: number[][]): number {
    let [s, cnt, mi] = [0, 0, Infinity];
    for (const row of matrix) {
        for (const x of row) {
            if (x < 0) {
                ++cnt;
            }
            const y = Math.abs(x);
            s += y;
            mi = Math.min(mi, y);
        }
    }
    return cnt % 2 === 0 ? s : s - 2 * mi;
}

Rust

impl Solution {
    pub fn max_matrix_sum(matrix: Vec<Vec<i32>>) -> i64 {
        let mut s = 0;
        let mut mi = i32::MAX;
        let mut cnt = 0;
        for row in matrix {
            for &x in row.iter() {
                cnt += if x < 0 { 1 } else { 0 };
                let y = x.abs();
                mi = mi.min(y);
                s += y as i64;
            }
        }
        if cnt % 2 == 0 {
            s
        } else {
            s - (mi as i64 * 2)
        }
    }
}

JavaScript

/**
 * @param {number[][]} matrix
 * @return {number}
 */
var maxMatrixSum = function (matrix) {
    let [s, cnt, mi] = [0, 0, Infinity];
    for (const row of matrix) {
        for (const x of row) {
            if (x < 0) {
                ++cnt;
            }
            const y = Math.abs(x);
            s += y;
            mi = Math.min(mi, y);
        }
    }
    return cnt % 2 === 0 ? s : s - 2 * mi;
};