| comments | difficulty | edit_url | tags | |||||
|---|---|---|---|---|---|---|---|---|
true |
困难 |
|
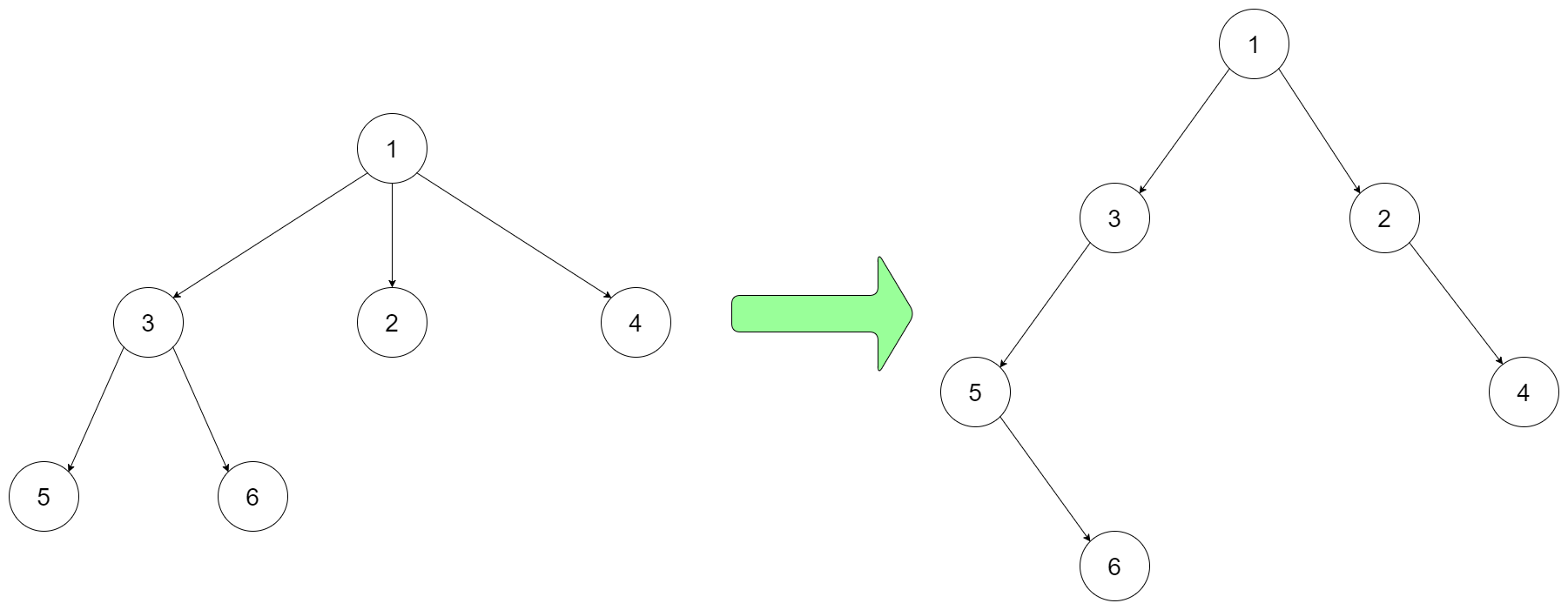
设计一个算法,可以将 N 叉树编码为二叉树,并能将该二叉树解码为原 N 叉树。一个 N 叉树是指每个节点都有不超过 N 个孩子节点的有根树。类似地,一个二叉树是指每个节点都有不超过 2 个孩子节点的有根树。你的编码 / 解码的算法的实现没有限制,你只需要保证一个 N 叉树可以编码为二叉树且该二叉树可以解码回原始 N 叉树即可。
例如,你可以将下面的 3-叉 树以该种方式编码:
输入:root = [1,null,3,2,4,null,5,6]
注意,上面的方法仅仅是一个例子,可能可行也可能不可行。你没有必要遵循这种形式转化,你可以自己创造和实现不同的方法。
示例 1:
输入:root = [1,null,3,2,4,null,5,6] 输出:[1,null,3,2,4,null,5,6]
示例 2:
输入:root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] 输出:[1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
示例 3:
输入:root = [] 输出:[]
提示:
N的范围在[1, 104]0 <= Node.val <= 104- N 叉树的高度小于等于
1000。 - 不要使用类成员 / 全局变量 / 静态变量来存储状态。你的编码和解码算法应是无状态的。