README_EN.md

1606. Find Servers That Handled Most Number of Requests

中文文档

Description

You have k servers numbered from 0 to k-1 that are being used to handle multiple requests simultaneously. Each server has infinite computational capacity but cannot handle more than one request at a time. The requests are assigned to servers according to a specific algorithm:

• The ith (0-indexed) request arrives.
• If all servers are busy, the request is dropped (not handled at all).
• If the (i % k)th server is available, assign the request to that server.
• Otherwise, assign the request to the next available server (wrapping around the list of servers and starting from 0 if necessary). For example, if the ith server is busy, try to assign the request to the (i+1)th server, then the (i+2)th server, and so on.

You are given a strictly increasing array arrival of positive integers, where arrival[i] represents the arrival time of the ith request, and another array load, where load[i] represents the load of the ith request (the time it takes to complete). Your goal is to find the busiest server(s). A server is considered busiest if it handled the most number of requests successfully among all the servers.

Return a list containing the IDs (0-indexed) of the busiest server(s). You may return the IDs in any order.

 

Example 1:

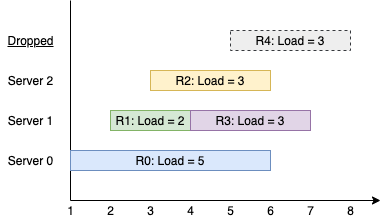
Input: k = 3, arrival = [1,2,3,4,5], load = [5,2,3,3,3] 
Output: [1] 
Explanation: 
All of the servers start out available.
The first 3 requests are handled by the first 3 servers in order.
Request 3 comes in. Server 0 is busy, so it's assigned to the next available server, which is 1.
Request 4 comes in. It cannot be handled since all servers are busy, so it is dropped.
Servers 0 and 2 handled one request each, while server 1 handled two requests. Hence server 1 is the busiest server.

Example 2:

Input: k = 3, arrival = [1,2,3,4], load = [1,2,1,2]
Output: [0]
Explanation: 
The first 3 requests are handled by first 3 servers.
Request 3 comes in. It is handled by server 0 since the server is available.
Server 0 handled two requests, while servers 1 and 2 handled one request each. Hence server 0 is the busiest server.

Example 3:

Input: k = 3, arrival = [1,2,3], load = [10,12,11]
Output: [0,1,2]
Explanation: Each server handles a single request, so they are all considered the busiest.

 

Constraints:

• 1 <= k <= 105
• 1 <= arrival.length, load.length <= 105
• arrival.length == load.length
• 1 <= arrival[i], load[i] <= 109
• arrival is strictly increasing.

Solutions

Python3

from sortedcontainers import SortedList


class Solution:
    def busiestServers(self, k: int, arrival: List[int], load: List[int]) -> List[int]:
        free = SortedList(range(k))
        busy = []
        cnt = [0] * k
        for i, (start, t) in enumerate(zip(arrival, load)):
            while busy and busy[0][0] <= start:
                free.add(busy[0][1])
                heappop(busy)
            if not free:
                continue
            j = free.bisect_left(i % k)
            if j == len(free):
                j = 0
            server = free[j]
            cnt[server] += 1
            heappush(busy, (start + t, server))
            free.remove(server)

        mx = max(cnt)
        return [i for i, v in enumerate(cnt) if v == mx]

Java

class Solution {
    public List<Integer> busiestServers(int k, int[] arrival, int[] load) {
        int[] cnt = new int[k];
        PriorityQueue<int[]> busy = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
        TreeSet<Integer> free = new TreeSet<>();
        for (int i = 0; i < k; ++i) {
            free.add(i);
        }
        for (int i = 0; i < arrival.length; ++i) {
            int start = arrival[i];
            int end = start + load[i];
            while (!busy.isEmpty() && busy.peek()[0] <= start) {
                free.add(busy.poll()[1]);
            }
            if (free.isEmpty()) {
                continue;
            }
            Integer server = free.ceiling(i % k);
            if (server == null) {
                server = free.first();
            }
            ++cnt[server];
            busy.offer(new int[] {end, server});
            free.remove(server);
        }
        int mx = 0;
        for (int v : cnt) {
            mx = Math.max(mx, v);
        }
        List<Integer> ans = new ArrayList<>();
        for (int i = 0; i < k; ++i) {
            if (cnt[i] == mx) {
                ans.add(i);
            }
        }
        return ans;
    }
}

Go

func busiestServers(k int, arrival, load []int) []int {
	free := redblacktree.NewWithIntComparator()
	for i := 0; i < k; i++ {
		free.Put(i, nil)
	}
	busy := hp{}
	cnt := make([]int, k)
	for i, t := range arrival {
		for len(busy) > 0 && busy[0].end <= t {
			free.Put(busy[0].server, nil)
			heap.Pop(&busy)
		}
		if free.Size() == 0 {
			continue
		}
		p, _ := free.Ceiling(i % k)
		if p == nil {
			p = free.Left()
		}
		server := p.Key.(int)
		cnt[server]++
		heap.Push(&busy, pair{t + load[i], server})
		free.Remove(server)
	}
	mx := 0
	for _, v := range cnt {
		if v > mx {
			mx = v
		}
	}
	var ans []int
	for i, v := range cnt {
		if v == mx {
			ans = append(ans, i)
		}
	}
	return ans
}

type pair struct{ end, server int }
type hp []pair

func (h hp) Len() int            { return len(h) }
func (h hp) Less(i, j int) bool  { return h[i].end < h[j].end }
func (h hp) Swap(i, j int)       { h[i], h[j] = h[j], h[i] }
func (h *hp) Push(v interface{}) { *h = append(*h, v.(pair)) }
func (h *hp) Pop() interface{}   { a := *h; v := a[len(a)-1]; *h = a[:len(a)-1]; return v }

...