Skip to content

Latest commit

 

History

History
283 lines (238 loc) · 7.94 KB

README_EN.md

File metadata and controls

283 lines (238 loc) · 7.94 KB
comments difficulty edit_url tags
true
Hard
Tree
Depth-First Search
Graph
Dynamic Programming

834. Sum of Distances in Tree

中文文档

Description

There is an undirected connected tree with n nodes labeled from 0 to n - 1 and n - 1 edges.

You are given the integer n and the array edges where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.

Return an array answer of length n where answer[i] is the sum of the distances between the ith node in the tree and all other nodes.

 

Example 1:

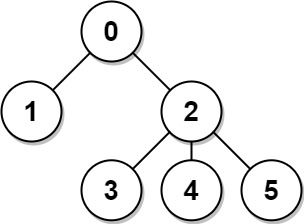
Input: n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
Output: [8,12,6,10,10,10]
Explanation: The tree is shown above.
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.
Hence, answer[0] = 8, and so on.

Example 2:

Input: n = 1, edges = []
Output: [0]

Example 3:

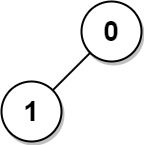
Input: n = 2, edges = [[1,0]]
Output: [1,1]

 

Constraints:

  • 1 <= n <= 3 * 104
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= ai, bi < n
  • ai != bi
  • The given input represents a valid tree.

Solutions

Solution 1: Tree DP (Re-rooting)

First, we run a DFS to calculate the size of each node's subtree, recorded in the array $size$, and compute the sum of distances from node $0$ to all other nodes, recorded in $ans[0]$.

Next, we run another DFS to enumerate the sum of distances from each node when it is considered as the root. Suppose the answer for the current node $i$ is $t$. When we move from node $i$ to node $j$, the sum of distances changes to $t - size[j] + n - size[j]$, meaning the sum of distances to node $j$ and its subtree nodes decreases by $size[j]$, while the sum of distances to other nodes increases by $n - size[j]$.

The time complexity is $O(n)$, and the space complexity is $O(n)$, where $n$ is the number of nodes in the tree.

Similar problems:

Python3

class Solution:
    def sumOfDistancesInTree(self, n: int, edges: List[List[int]]) -> List[int]:
        def dfs1(i: int, fa: int, d: int):
            ans[0] += d
            size[i] = 1
            for j in g[i]:
                if j != fa:
                    dfs1(j, i, d + 1)
                    size[i] += size[j]

        def dfs2(i: int, fa: int, t: int):
            ans[i] = t
            for j in g[i]:
                if j != fa:
                    dfs2(j, i, t - size[j] + n - size[j])

        g = defaultdict(list)
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)

        ans = [0] * n
        size = [0] * n
        dfs1(0, -1, 0)
        dfs2(0, -1, ans[0])
        return ans

Java

class Solution {
    private int n;
    private int[] ans;
    private int[] size;
    private List<Integer>[] g;

    public int[] sumOfDistancesInTree(int n, int[][] edges) {
        this.n = n;
        g = new List[n];
        ans = new int[n];
        size = new int[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        for (var e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        dfs1(0, -1, 0);
        dfs2(0, -1, ans[0]);
        return ans;
    }

    private void dfs1(int i, int fa, int d) {
        ans[0] += d;
        size[i] = 1;
        for (int j : g[i]) {
            if (j != fa) {
                dfs1(j, i, d + 1);
                size[i] += size[j];
            }
        }
    }

    private void dfs2(int i, int fa, int t) {
        ans[i] = t;
        for (int j : g[i]) {
            if (j != fa) {
                dfs2(j, i, t - size[j] + n - size[j]);
            }
        }
    }
}

C++

class Solution {
public:
    vector<int> sumOfDistancesInTree(int n, vector<vector<int>>& edges) {
        vector<vector<int>> g(n);
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].push_back(b);
            g[b].push_back(a);
        }
        vector<int> ans(n);
        vector<int> size(n);

        function<void(int, int, int)> dfs1 = [&](int i, int fa, int d) {
            ans[0] += d;
            size[i] = 1;
            for (int& j : g[i]) {
                if (j != fa) {
                    dfs1(j, i, d + 1);
                    size[i] += size[j];
                }
            }
        };

        function<void(int, int, int)> dfs2 = [&](int i, int fa, int t) {
            ans[i] = t;
            for (int& j : g[i]) {
                if (j != fa) {
                    dfs2(j, i, t - size[j] + n - size[j]);
                }
            }
        };

        dfs1(0, -1, 0);
        dfs2(0, -1, ans[0]);
        return ans;
    }
};

Go

func sumOfDistancesInTree(n int, edges [][]int) []int {
	g := make([][]int, n)
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	ans := make([]int, n)
	size := make([]int, n)
	var dfs1 func(i, fa, d int)
	dfs1 = func(i, fa, d int) {
		ans[0] += d
		size[i] = 1
		for _, j := range g[i] {
			if j != fa {
				dfs1(j, i, d+1)
				size[i] += size[j]
			}
		}
	}
	var dfs2 func(i, fa, t int)
	dfs2 = func(i, fa, t int) {
		ans[i] = t
		for _, j := range g[i] {
			if j != fa {
				dfs2(j, i, t-size[j]+n-size[j])
			}
		}
	}
	dfs1(0, -1, 0)
	dfs2(0, -1, ans[0])
	return ans
}

TypeScript

function sumOfDistancesInTree(n: number, edges: number[][]): number[] {
    const g: number[][] = Array.from({ length: n }, () => []);
    for (const [a, b] of edges) {
        g[a].push(b);
        g[b].push(a);
    }
    const ans: number[] = new Array(n).fill(0);
    const size: number[] = new Array(n).fill(0);
    const dfs1 = (i: number, fa: number, d: number) => {
        ans[0] += d;
        size[i] = 1;
        for (const j of g[i]) {
            if (j !== fa) {
                dfs1(j, i, d + 1);
                size[i] += size[j];
            }
        }
    };
    const dfs2 = (i: number, fa: number, t: number) => {
        ans[i] = t;
        for (const j of g[i]) {
            if (j !== fa) {
                dfs2(j, i, t - size[j] + n - size[j]);
            }
        }
    };
    dfs1(0, -1, 0);
    dfs2(0, -1, ans[0]);
    return ans;
}