2445. 值为 1 的节点数 🔒

English Version

题目描述

有一个 无向 树，有 n 个节点，节点标记为从 1 到 n ，还有 n - 1 条边。给定整数 n。标记为 v 的节点的父节点是标记为 floor (v / 2) 的节点。树的根节点是标记为 1 的节点。

• 例如，如果 n = 7，那么标记为 3 的节点将标记 floor(3 / 2) = 1 的节点作为其父节点，标记为 7 的节点将标记 floor(7 / 2) = 3 的节点作为其父节点。

你还得到一个整数数组 queries。最初，每个节点的值都是 0。对于每个查询 queries[i]，您应该翻转节点标记为 queries[i] 的子树中的所有值。

在 处理完所有查询后，返回值为 1 的节点总数。

注意:

• 翻转节点的值意味着值为 0 的节点变为 1，反之亦然。
• floor(x) 相当于将 x 舍入到最接近的整数。

 

示例 1:

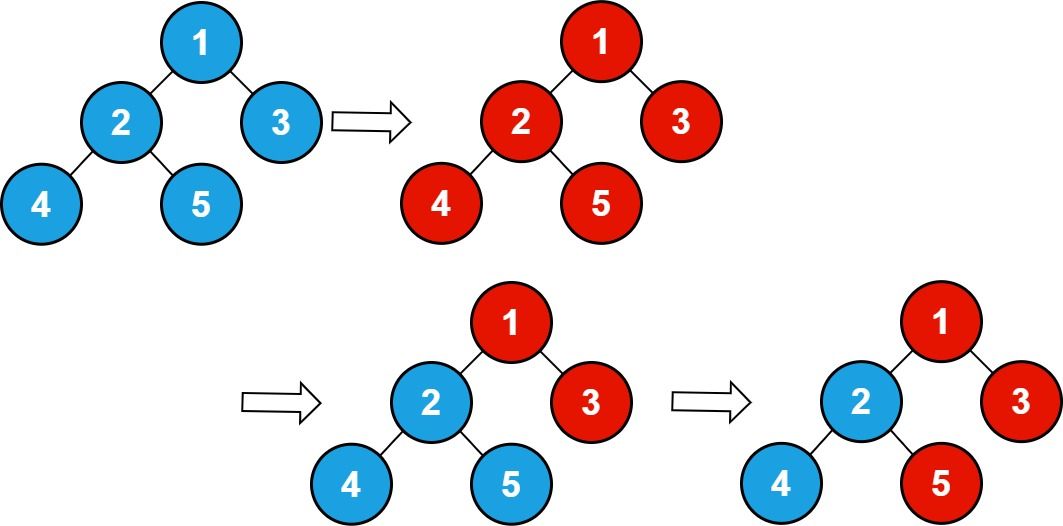
输入: n = 5 , queries = [1,2,5]
输出: 3
解释: 上图显示了执行查询后的树结构及其状态。蓝色节点表示值 0，红色节点表示值 1。
在处理查询之后，有三个红色节点 (值为 1 的节点): 1、3、5。

示例 2:

输入: n = 3, queries = [2,3,3]
输出: 1
解释: 上图显示了执行查询后的树结构及其状态。蓝色节点表示值 0，红色节点表示值 1。
在处理查询之后，有一个红色节点 (值为 1 的节点): 2。

 

提示:

• 1 <= n <= 105
• 1 <= queries.length <= 105
• 1 <= queries[i] <= n

解法

方法一：模拟

根据题意，我们可以模拟每次查询的过程，即将查询节点及其子树的节点值反转。最后统计节点值为 1 的节点个数即可。

这里有一个优化点，每个节点及其对应的子树，如果经过了偶数次查询，那么节点值不会发生变化，因此我们可以记录每个节点的查询次数，对于奇数次查询的节点及其子树，才进行反转。

时间复杂度 $O(n \times \log n)$，空间复杂度 $O(n)$。其中 $n$ 为节点个数。

class Solution:
    def numberOfNodes(self, n: int, queries: List[int]) -> int:
        def dfs(i):
            if i > n:
                return
            tree[i] ^= 1
            dfs(i << 1)
            dfs(i << 1 | 1)

        tree = [0] * (n + 1)
        cnt = Counter(queries)
        for i, v in cnt.items():
            if v & 1:
                dfs(i)
        return sum(tree)

class Solution {
    private int[] tree;

    public int numberOfNodes(int n, int[] queries) {
        tree = new int[n + 1];
        int[] cnt = new int[n + 1];
        for (int v : queries) {
            ++cnt[v];
        }
        for (int i = 0; i < n + 1; ++i) {
            if (cnt[i] % 2 == 1) {
                dfs(i);
            }
        }
        int ans = 0;
        for (int i = 0; i < n + 1; ++i) {
            ans += tree[i];
        }
        return ans;
    }

    private void dfs(int i) {
        if (i >= tree.length) {
            return;
        }
        tree[i] ^= 1;
        dfs(i << 1);
        dfs(i << 1 | 1);
    }
}

class Solution {
public:
    int numberOfNodes(int n, vector<int>& queries) {
        vector<int> tree(n + 1);
        vector<int> cnt(n + 1);
        for (int v : queries) ++cnt[v];
        function<void(int)> dfs = [&](int i) {
            if (i > n) return;
            tree[i] ^= 1;
            dfs(i << 1);
            dfs(i << 1 | 1);
        };
        for (int i = 0; i < n + 1; ++i) {
            if (cnt[i] & 1) {
                dfs(i);
            }
        }
        return accumulate(tree.begin(), tree.end(), 0);
    }
};

func numberOfNodes(n int, queries []int) int {
	tree := make([]int, n+1)
	cnt := make([]int, n+1)
	for _, v := range queries {
		cnt[v]++
	}
	var dfs func(int)
	dfs = func(i int) {
		if i > n {
			return
		}
		tree[i] ^= 1
		dfs(i << 1)
		dfs(i<<1 | 1)
	}
	for i, v := range cnt {
		if v%2 == 1 {
			dfs(i)
		}
	}
	ans := 0
	for _, v := range tree {
		ans += v
	}
	return ans
}