README_EN.md

276. Paint Fence 🔒

中文文档

Description

You are painting a fence of n posts with k different colors. You must paint the posts following these rules:

• Every post must be painted exactly one color.
• There cannot be three or more consecutive posts with the same color.

Given the two integers n and k, return the number of ways you can paint the fence.

 

Example 1:

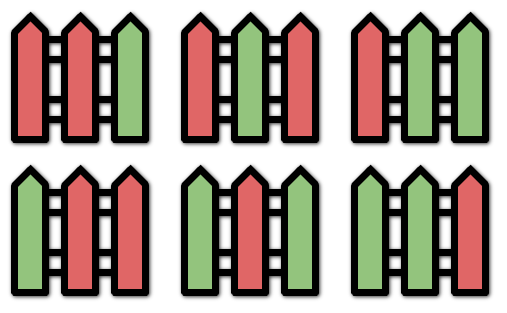
Input: n = 3, k = 2
Output: 6
Explanation: All the possibilities are shown.
Note that painting all the posts red or all the posts green is invalid because there cannot be three posts in a row with the same color.

Example 2:

Input: n = 1, k = 1
Output: 1

Example 3:

Input: n = 7, k = 2
Output: 42

 

Constraints:

• 1 <= n <= 50
• 1 <= k <= 105
• The testcases are generated such that the answer is in the range [0, 231 - 1] for the given n and k.

Solutions

Solution 1: Dynamic Programming

We define $f[i]$ to represent the number of ways to paint the fence posts from $[0..i]$ such that the last two posts have different colors, and $g[i]$ to represent the number of ways to paint the fence posts from $[0..i]$ such that the last two posts have the same color. Initially, $f[0]=k$ and $g[0]=0$.

When $i>0$, we have the following state transition equations:

$$\begin{array}{rl}f[i]& =(f[i-1]+g[i-1])\times (k-1)\\ g[i]& =f[i-1]\end{array}$$

The final answer is $f[n-1]+g[n-1]$.

The time complexity is $O(n)$ and the space complexity is $O(n)$, where $n$ is the number of fence posts.

class Solution:
    def numWays(self, n: int, k: int) -> int:
        f = [0] * n
        g = [0] * n
        f[0] = k
        for i in range(1, n):
            f[i] = (f[i - 1] + g[i - 1]) * (k - 1)
            g[i] = f[i - 1]
        return f[-1] + g[-1]

class Solution {
    public int numWays(int n, int k) {
        int[] f = new int[n];
        int[] g = new int[n];
        f[0] = k;
        for (int i = 1; i < n; ++i) {
            f[i] = (f[i - 1] + g[i - 1]) * (k - 1);
            g[i] = f[i - 1];
        }
        return f[n - 1] + g[n - 1];
    }
}

class Solution {
public:
    int numWays(int n, int k) {
        vector<int> f(n);
        vector<int> g(n);
        f[0] = k;
        for (int i = 1; i < n; ++i) {
            f[i] = (f[i - 1] + g[i - 1]) * (k - 1);
            g[i] = f[i - 1];
        }
        return f[n - 1] + g[n - 1];
    }
};

func numWays(n int, k int) int {
	f := make([]int, n)
	g := make([]int, n)
	f[0] = k
	for i := 1; i < n; i++ {
		f[i] = (f[i-1] + g[i-1]) * (k - 1)
		g[i] = f[i-1]
	}
	return f[n-1] + g[n-1]
}

function numWays(n: number, k: number): number {
    const f: number[] = Array(n).fill(0);
    const g: number[] = Array(n).fill(0);
    f[0] = k;
    for (let i = 1; i < n; ++i) {
        f[i] = (f[i - 1] + g[i - 1]) * (k - 1);
        g[i] = f[i - 1];
    }
    return f[n - 1] + g[n - 1];
}

Solution 2: Dynamic Programming (Space Optimization)

We notice that $f[i]$ and $g[i]$ are only related to $f[i-1]$ and $g[i-1]$. Therefore, we can use two variables $f$ and $g$ to record the values of $f[i-1]$ and $g[i-1]$ respectively, thus optimizing the space complexity to $O(1)$.

class Solution:
    def numWays(self, n: int, k: int) -> int:
        f, g = k, 0
        for _ in range(n - 1):
            ff = (f + g) * (k - 1)
            g = f
            f = ff
        return f + g

class Solution {
    public int numWays(int n, int k) {
        int f = k, g = 0;
        for (int i = 1; i < n; ++i) {
            int ff = (f + g) * (k - 1);
            g = f;
            f = ff;
        }
        return f + g;
    }
}

class Solution {
public:
    int numWays(int n, int k) {
        int f = k, g = 0;
        for (int i = 1; i < n; ++i) {
            int ff = (f + g) * (k - 1);
            g = f;
            f = ff;
        }
        return f + g;
    }
};

func numWays(n int, k int) int {
	f, g := k, 0
	for i := 1; i < n; i++ {
		f, g = (f+g)*(k-1), f
	}
	return f + g
}

function numWays(n: number, k: number): number {
    let [f, g] = [k, 0];
    for (let i = 1; i < n; ++i) {
        const ff = (f + g) * (k - 1);
        g = f;
        f = ff;
    }
    return f + g;
}