|
| 1 | +# 802. Find Eventual Safe States |
| 2 | + |
| 3 | +- Difficulty: Medium. |
| 4 | +- Related Topics: Depth-First Search, Breadth-First Search, Graph, Topological Sort. |
| 5 | +- Similar Questions: Build a Matrix With Conditions. |
| 6 | + |
| 7 | +## Problem |
| 8 | + |
| 9 | +There is a directed graph of `n` nodes with each node labeled from `0` to `n - 1`. The graph is represented by a **0-indexed** 2D integer array `graph` where `graph[i]` is an integer array of nodes adjacent to node `i`, meaning there is an edge from node `i` to each node in `graph[i]`. |
| 10 | + |
| 11 | +A node is a **terminal node** if there are no outgoing edges. A node is a **safe node** if every possible path starting from that node leads to a **terminal node** (or another safe node). |
| 12 | + |
| 13 | +Return **an array containing all the **safe nodes** of the graph**. The answer should be sorted in **ascending** order. |
| 14 | + |
| 15 | + |
| 16 | +Example 1: |
| 17 | + |
| 18 | +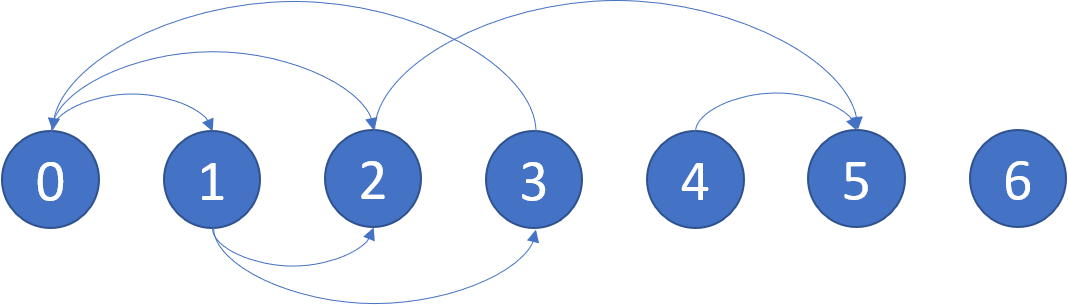 |
| 19 | + |
| 20 | +``` |
| 21 | +Input: graph = [[1,2],[2,3],[5],[0],[5],[],[]] |
| 22 | +Output: [2,4,5,6] |
| 23 | +Explanation: The given graph is shown above. |
| 24 | +Nodes 5 and 6 are terminal nodes as there are no outgoing edges from either of them. |
| 25 | +Every path starting at nodes 2, 4, 5, and 6 all lead to either node 5 or 6. |
| 26 | +``` |
| 27 | + |
| 28 | +Example 2: |
| 29 | + |
| 30 | +``` |
| 31 | +Input: graph = [[1,2,3,4],[1,2],[3,4],[0,4],[]] |
| 32 | +Output: [4] |
| 33 | +Explanation: |
| 34 | +Only node 4 is a terminal node, and every path starting at node 4 leads to node 4. |
| 35 | +``` |
| 36 | + |
| 37 | + |
| 38 | +**Constraints:** |
| 39 | + |
| 40 | + |
| 41 | + |
| 42 | +- `n == graph.length` |
| 43 | + |
| 44 | +- `1 <= n <= 104` |
| 45 | + |
| 46 | +- `0 <= graph[i].length <= n` |
| 47 | + |
| 48 | +- `0 <= graph[i][j] <= n - 1` |
| 49 | + |
| 50 | +- `graph[i]` is sorted in a strictly increasing order. |
| 51 | + |
| 52 | +- The graph may contain self-loops. |
| 53 | + |
| 54 | +- The number of edges in the graph will be in the range `[1, 4 * 104]`. |
| 55 | + |
| 56 | + |
| 57 | + |
| 58 | +## Solution |
| 59 | + |
| 60 | +```javascript |
| 61 | +/** |
| 62 | + * @param {number[][]} graph |
| 63 | + * @return {number[]} |
| 64 | + */ |
| 65 | +var eventualSafeNodes = function(graph) { |
| 66 | + var map = Array(graph.length); |
| 67 | + var path = Array(graph.length); |
| 68 | + var res = []; |
| 69 | + for (var i = 0; i < graph.length; i++) { |
| 70 | + if (isSafeNode(i, graph, map, path)) { |
| 71 | + res.push(i); |
| 72 | + } |
| 73 | + } |
| 74 | + return res; |
| 75 | +}; |
| 76 | + |
| 77 | +var isSafeNode = function(i, graph, map, path) { |
| 78 | + if (graph[i].length === 0 || map[i] === 1) return true; |
| 79 | + if (map[i] === 2 || path[i] === 1) return false; |
| 80 | + path[i] = 1; |
| 81 | + for (var j = 0; j < graph[i].length; j++) { |
| 82 | + var index = graph[i][j]; |
| 83 | + if (!isSafeNode(index, graph, map, path)) { |
| 84 | + path[i] = 0; |
| 85 | + map[i] = 2; |
| 86 | + return false; |
| 87 | + } |
| 88 | + } |
| 89 | + path[i] = 0; |
| 90 | + map[i] = 1; |
| 91 | + return true; |
| 92 | +}; |
| 93 | +``` |
| 94 | + |
| 95 | +**Explain:** |
| 96 | + |
| 97 | +DFS (Depth First Search). |
| 98 | + |
| 99 | +**Complexity:** |
| 100 | + |
| 101 | +`n` nodes, `m` edges. |
| 102 | + |
| 103 | +* Time complexity : O(n + m). |
| 104 | +* Space complexity : O(n + m). |
0 commit comments