|
| 1 | + |
| 2 | +## Inverview-62:队列的最大值 |
| 3 | + |
| 4 | +**题目**:0,1,,n-1 这 n 个数字排成一个圆圈,从数字 0 开始,每次从这个圆圈里删除第 m 个数字。求出这个圆圈里剩下的最后一个数字。例如,0、1、2、3、4 这 5 个数字组成一个圆圈,从数字 0 开始每次删除第 3 个数字,则删除的前 4 个数字依次是 2、0、4、1,因此最后剩下的数字是 3。 |
| 5 | + |
| 6 | +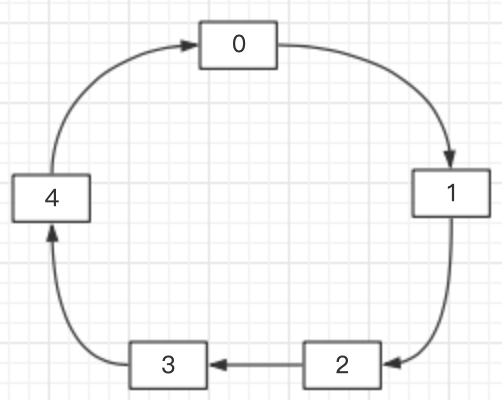 |
| 7 | + |
| 8 | +这就是一个约瑟夫环问题。 |
| 9 | + |
| 10 | +**解题思路** |
| 11 | + |
| 12 | +解题的一种方法是可以用环形链表来模拟圆圈,然后循环就可以解决了。但会发现环形链表重复遍历了很多遍,总的时间复杂度是 O(mn)。 |
| 13 | + |
| 14 | +还有一种方法是查看数字之间的规律,如下所述: |
| 15 | + |
| 16 | +- **首先**我们定义一个关于 n 和m的方程 F(n,m),表示每次在 n 个数字 0 到 n-1 中删除第 m 个数字最后剩下的数字。在这 n 个数字中,第一个被删除的数字是 (m-1)%n。为了简单起见,我们把 (m-1)%n 记为 k。 |
| 17 | + |
| 18 | +- **删除** k 之后剩下的 n-1 个数字,并且下一次删除从数字 k+1 开始计数循环删除第 m 个数字,直到只剩下一个数字为止。我们可以定义这样的式子,F(n,m)=F(n-1,m) |
| 19 | + |
| 20 | +- **找规律**: 接下来我们把删除过后的数字与从 0 开始计数的 n-2 的序列进行一一**映射**。 |
| 21 | + $$ |
| 22 | + \begin{array}{l}{k+1 \rightarrow 0} \\ {k+2 \rightarrow 1} \\ {\cdots} \\ {n-1 \rightarrow n-k-2} \\ {0 \rightarrow n-k-1} \\ {1 \rightarrow n-k} \\ {\cdots} \\ {k-1 \quad \rightarrow \quad n-2}\end{array} |
| 23 | + $$ |
| 24 | + 会发现一个映射规律公式,P(x)=(x-k-1)%n。它表示如果映射前的数字是x,那么映射后的数字是 (x-k-1)%n。同样的,逆映射就是 Q(x)=(x+k+1)%n。 |
| 25 | + |
| 26 | +- 接下来就是带入 F(n-1,m)。 |
| 27 | + |
| 28 | + F(n-1,m) = Q[F(n-1,m)] = [F(n-1,m)+k+1]%n。 |
| 29 | + |
| 30 | + 把 k=(m-1)%n 代入 |
| 31 | + |
| 32 | + F(n,m)=F(n-1,m) = [F(n-1,m)+m]%n |
| 33 | + |
| 34 | +- **最终**我们就可以得到如下式子: |
| 35 | + $$ |
| 36 | + f(n, m)=\left\{\begin{array}{ll}{0} & {n=1} \\ {[f(n-1, m)+m]^{0 / 0} n} & {n>1}\end{array}\right. |
| 37 | + $$ |
| 38 | + 根据这个公式我们就可以进行编程实现了,递归和循环都可以。 |
| 39 | + |
| 40 | +**以下代码可提交至LeetCode:** |
| 41 | + |
| 42 | +[https://leetcode-cn.com/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof/](https://leetcode-cn.com/problems/yuan-quan-zhong-zui-hou-sheng-xia-de-shu-zi-lcof/) |
| 43 | + |
| 44 | +```python |
| 45 | +class Solution: |
| 46 | + |
| 47 | + def lastRemaining(self, n: int, m: int) -> int: |
| 48 | + if n == 1: |
| 49 | + return 0 |
| 50 | + |
| 51 | + last = 0 |
| 52 | + for i in range(2, n + 1): |
| 53 | + last = (last + m) % i |
| 54 | + |
| 55 | + return last |
| 56 | + |
| 57 | +n = 5 |
| 58 | +m = 3 |
| 59 | +s = Solution() |
| 60 | +print(s.lastRemaining(n, m)) |
| 61 | +``` |
| 62 | + |
| 63 | +结果如下: |
| 64 | + |
| 65 | +``` |
| 66 | +3 |
| 67 | +``` |
| 68 | + |
| 69 | + |
| 70 | + |
| 71 | + |
0 commit comments